はじめに
みなさんはじめまして。本コースを担当するゴフェルテックの川西です。ゴフェルテックは FPGA を使用して暗号を安全に実装する方法を岡山大学と共同で研究開発しています。
ここで注意して頂きたいのは「安全な暗号」の研究ではなく「暗号を安全に実装する方法」を研究しているところです。いまひとつピンとこないかと思いますが、実は FPGA に暗号機能を搭載するとき、十分に注意を払わないと「サイドチャネル攻撃」と呼ばれる攻撃に対して脆弱な暗号機能になってしまい、暗号で最も重要な暗号鍵を攻撃者に盗まれる危険性が高くなります。
サイドチャネル攻撃の対策を一切おこなわずに暗号機能を FPGA に組み込んだ場合、AES 暗号だと 1 日から数日で鍵を盗むことが出来ます。また、鍵共有に使用されている公開鍵暗号 (RSA 暗号や楕円曲線暗号) の場合、鍵をオシロスコープで読み取ることが出来てしまいます。
本コースでは、暗号の概要を解説するところから始め、サイドチャネル攻撃による危険性に触れていきたいと思います。
なぜ FPGA で暗号か ?
暗号の解説に入る前に、なぜ FPGA に暗号機能なのかについて、筆者の考える背景を説明します。
現在、世間は IoT 全盛です。みなさんご存知の通り、あらゆるものがネットワークに接続されるようになってきました。家電やカメラ、自動車までもがネットワークに接続されています。
信号機をネットワークに接続してディープラーニングと組み合わせることで最適に制御するといった研究も各所で行われているようです。ここでは、信号機をネットワークに接続して制御する例を考えてみます。ネットワークに接続されている上位機器からの指令に従ってそれぞれの信号機にある制御装置が信号機を操作するような構成です。
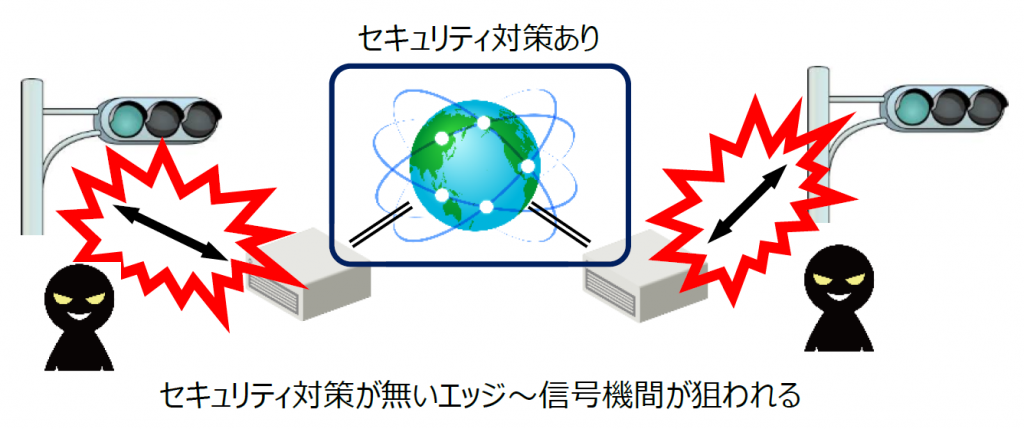
ネットワークは TLS といったセキュアなプロトコルを使用することでデータの盗聴や改竄を防ぐことが出来ます。しかし、各信号機に取り付けられた制御装置と信号機の間で行われるローカルな通信にセキュリティ対策を組み込まず、暗号化されない生データで通信を行うと危険です。攻撃者がこの通信を盗聴したり改竄することで信号機を自由に操作することが可能になり、悪意を持った攻撃者によって全ての信号を同時に青にして交通事故を引き起こすことまで可能になってしまいます。
IoT による通信の負荷を軽減するため、末端の制御装置内で行う処理 (エッジコンピューティング) が増えてきています。様々な処理に対応できる FPGA が活躍できるのが、まさにこの部分だと思いますが、セキュリティを疎かにすると … 大変です。
そこで登場するのが暗号です。通信を暗号化することで悪意を持った攻撃者によるデータの改竄や盗聴から守ることができます。
悪意を持った攻撃者はシステムの中で最も弱い部分に攻撃を仕掛けてきます。上の例で取り上げたエッジ処理などは、色々な処理に柔軟に対応できる FPGA が活躍できる部分ですが、セキュリティ対策を施さなかったり、安易な対策だと攻撃者の標的になりシステム全体が危険になります。FPGA が攻撃の入り口にならないよう、安全な通信を実現出来る暗号機能を FPGA で実現することが重要だと考えています。
用語の定義
暗号とは、「あるデータ」を「何らかの方法」で「第三者には意味が分からないデータ」に変換することと言えます。ただし、特定の情報を持っている人のみが変換後のデータを元のデータに戻すことができることが単なるデータ変換とは異なります。
暗号について解説するとき、微妙に異なる用語が使用されることがあるため、本コース内で使用する用語を決めておきます。
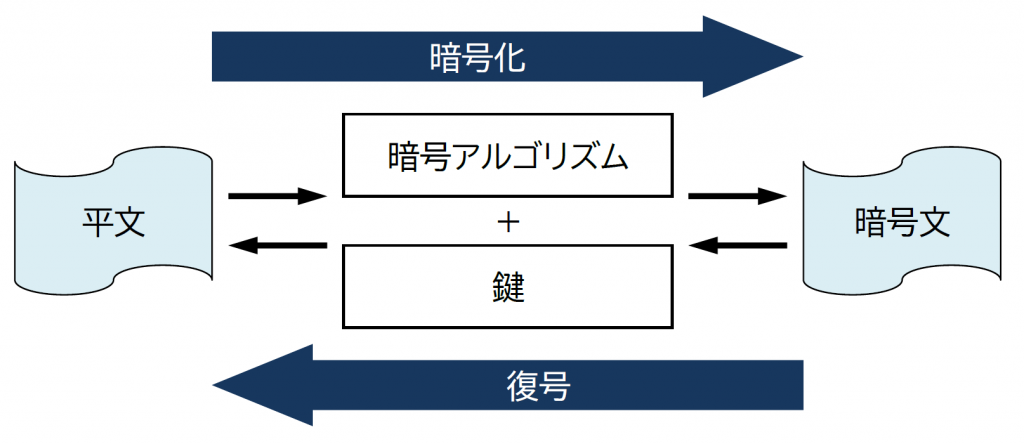
| 平文 | 暗号化される前のデータ。白文、テキストと呼ばれる場合もあります。 |
| 暗号化 | 平文を暗号文に変換すること。 |
| 復号 | 暗号文を平文に変換すること。暗号化と同じように復号化と表現されることもありますが、ここでは復号とします。 |
| 暗号アルゴリズム | 暗号化 / 復号で使用される暗号の方式。本コースでは AES 暗号、楕円曲線暗号が登場します。 |
| 鍵 (暗号鍵) | 暗号化や復号の時に使用するデータ |
| 暗号文 | 平文を暗号によって変換した変換後のデータ |
暗号の種類
暗号アルゴリズムを大きく二つに分けると共通鍵暗号と公開鍵暗号があります。共通鍵暗号は秘密鍵暗号とも呼ばれますが、公開鍵暗号で使用される秘密鍵と混同し易いため、本コースでは共通鍵暗号とします。
また、暗号には平文を暗号文に変換して相手に渡し、受け取ったデータを平文に戻すという使用方法以外にもデータの改竄を検知するためのハッシュ関数や成りすましを防ぐためのメッセージ認証コードなどもあります。
接続されている通信相手が正当な通信相手であることを確認するための認証は安全な通信の重要な要素ですが、本コースでは FPGA による暗号機能に焦点を当て、ハッシュ関数やメッセージ認証コードには触れません。
共通鍵暗号
家のドアを正しい鍵を持っている人であれば開けたり、閉めたりできるのと同じように、暗号化も復号も同じ鍵 (暗号鍵) で行うのが共通鍵暗号です。多くの人が、暗号と聞いて直感的に考えるのが共通鍵暗号です。
古代ローマ時代、文字を決まった数シフトさせることで暗号化する換字式暗号 (シーザー暗号) が使われていました。例えば、「アルファベットを 3 文字シフトする」と決めれば A → D、G → J になります。この方法で暗号化すると「FPGA」が「ISJD」になり、逆に 3 文字シフトすることで復号することができます。
シーザー暗号も共通鍵暗号であり、上の例では「FPGA」が平文、「ISJD」が暗号文、暗号アルゴリズムが「x 文字シフト」、鍵が「3」になります。共通の鍵 (= 文字のシフト数) を持っている場合にのみ暗号化と復号が成立するので共通鍵暗号です。
現在、世界で最も使用されている共通鍵暗号は「AES 暗号」であり、インターネットや WiFi, USB メモリの暗号機能などあらゆるところで使われてます。他にも Camellia や軽量暗号の SIMON/SPECK, Piccoloといった共通鍵暗号もあります。それぞれで暗号アルゴリズムは異なりますが、共通鍵暗号の基本的な動作を一言で表現すれば、データを「ゴチャゴチャに混ぜる」ことです。
本コースでは、128ビットの AES 暗号について次回以降に解説していきます。
公開鍵暗号
公開鍵暗号は「暗号化するときの鍵と復号するときの鍵が異なる暗号」と解説されることが多いですが、いまひとつピンとこない方が多いのではないでしょうか。この内容を分かり易くするため、あえて数式を使って説明します。
RSA 暗号や楕円曲線暗号は一方向関数という性質を持った関数を使用するため、よく見かける (ちゃんとした) 説明では剰余計算 (mod) や素数が出てきて取っつき難い雰囲気が出ています。しかし、公開鍵暗号の動作を説明するために一方向関数自体はあまり重要でないため、思い切って掛け算が一方向関数だとして説明します。 普通の掛け算では「A × B = C」の A と C が分かると B を計算することができ、A = 5、C = 15 なら B = 3 であることは簡単に求まります。一方向関数というのは、これができない関数であり「A × B = C」で A と C が分かっても B を求めることができない関数です。
掛け算を一方向関数であると仮定して、アリスとボブが同じデータを共有することを考えます。
余談ですが、暗号の説明をする際、慣例として登場人物の名前が決まっていてデータをやり取りする人物にアリスとボブが使われ、他にも盗聴者がイブだったり、攻撃者がマロニーだったりします。
具体的な動作を説明する前に用語を説明しておきます。
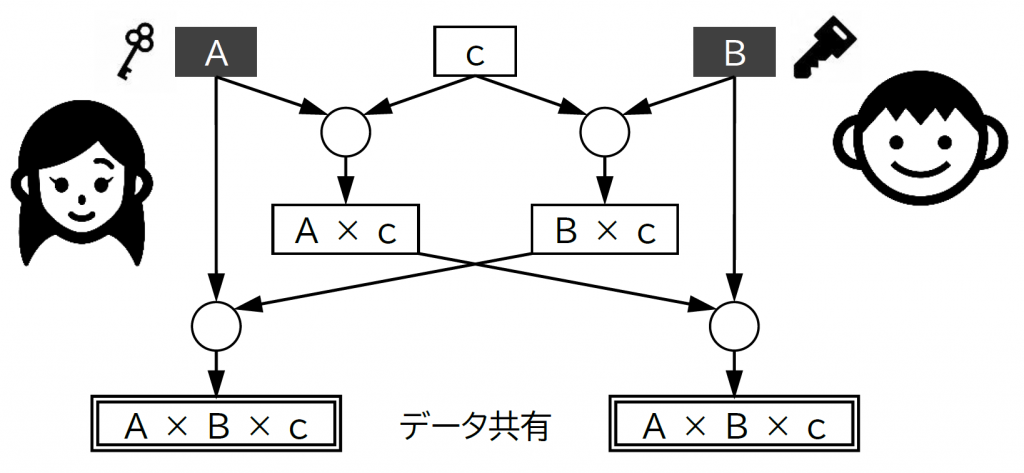
公開鍵暗号では2種類の鍵が登場します。秘密鍵は本人以外に知られてはいけない秘密の鍵であり、公開鍵は第三者に知られても問題ない公開可能な鍵です。
1. アリスが 自分の秘密鍵「A」と適当な値「c」を決めて「A × c」を計算します。この時、「c」と「A × c」が公開鍵 (公開鍵が複数の値なので公開鍵ペアと呼ばれます) であり、ボブ以外に知られても構いません。「A」はアリスの秘密鍵であり、他人に知られないようにしておく必要があります。ここで関数「×」を一方向関数としているので、「A × c」と「c」が分かっても「A」を割り出すことはできません。
2. ボブは自分の秘密鍵「B」を決めます。アリスから受け取った公開鍵ペアの「c」を使って「B × c」を計算し、アリスに教えます。この「B × c」がボブの公開鍵になり、アリス以外に知られても問題ありません。繰り返しになりますが、「B × c」と「c」が分かっても「B」が割り出せないためです。
3. アリスは自分の秘密鍵「A」とボブの公開鍵「B × c」を使って「A × B × c」を計算します。
4. ボブは自分の秘密鍵「B」とアリスの公開鍵「A × c」を使って「A × B × c」を計算します。
結果、アリスとボブは「A × B × c」を共有することができました。「×」が一方向関数なので公開鍵「c」、「A × c」、「B × c」が分かっても、アリスとボブ以外は「A × B × c」を求めることができません。
この動作説明では使用する鍵を適当に決めていましたが、実際の暗号では使用できる値に条件があるなど正確でない部分があります。しかし、一方向関数を使用して通信相手とのみデータを共有する動作は上記の通りです。
この例は、公開鍵暗号を使用したディフィー・ヘルマン鍵共有を簡単に説明したものです。公開鍵暗号は例に挙げた鍵共有以外にも改竄を検知するための署名や成りすましを防ぐ認証にも使用されます。本コースでは、公開鍵暗号として楕円曲線暗号を取り上げていきます。
実際に行われる暗号通信
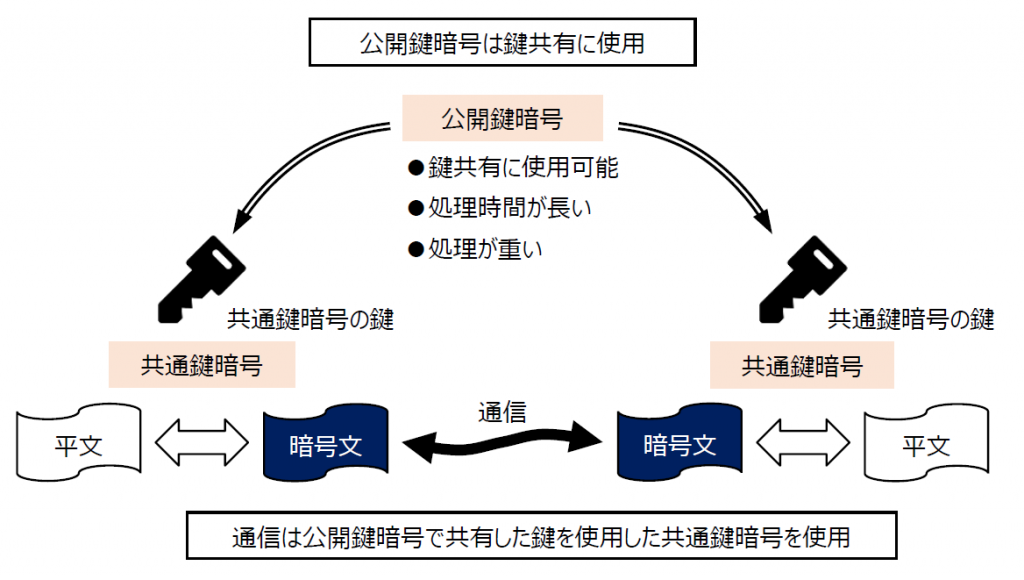
インターネットや Bluetooth など、実際の通信では共通鍵暗号と公開鍵暗号を組み合わせて使用しています。
共通鍵暗号と公開鍵暗号の最大の違いは計算時間です。共通鍵暗号に対して、公開鍵暗号は重い計算を複数回おこなう必要があるため、処理時間が長くなります。そこで、公開鍵暗号を使用して共通鍵暗号の暗号鍵を通信相手と共有し、共有後は処理の速い共通鍵暗号で通信します。
少し脱線しますが、公開鍵暗号が論文で発表されたのは1970年代の RSA 暗号が最初であり、それまでは共通鍵暗号のみを使用して暗号通信を行っていました。
共通鍵暗号しか使えない場合、暗号に使用する鍵を通信相手とどうやって共有するのかが問題になります (鍵配送問題)。鍵が共有できていなければ暗号を使った安全な通信ができません。また、暗号鍵は一度共有すれば良いわけではなく、安全性を考えると長期間同じ鍵を使うわけにもいきません。定期的に鍵を更新する必要がありますが、変更する鍵を郵便で送るのは危険です。
安全に鍵を共有するため、重要なデータを取り扱う機関は地球の裏側であっても鍵配送を人力で行っていました。政府機関や銀行では、世界中に鍵を届ける専門の組織があり「今週の鍵はこれですよ」と人間が配達していたため、ものすごいコストが掛かっていたそうです。
公開鍵暗号が開発されたことで離れた場所でも通信によって安全に鍵共有が可能になり、インターネットでクレジットカード情報や銀行口座情報などの重要なデータがやり取りできるようになりました。通信相手が成りすましでないことを証明する認証などにも公開鍵暗号が使用されており、公開鍵暗号は現在の通信環境に多大な恩恵をもたらしていると言えます。
独自暗号は危険
暗号は大きく分けると共通鍵暗号と公開鍵暗号があると説明しましたが、共通鍵暗号、公開鍵暗号それぞれにも多くの種類があります。
次回以降で取り上げるのは世界標準として使用されている AES 暗号と楕円曲線暗号ですが、この「世界標準」が重要だということを今回の最後に解説します。
FPGA ~ FPGA 間で行うデータ通信を盗聴や改竄から保護することを考えます。このとき、「標準化されている暗号はなんだか難しそうなので、適当にデータを入れ替えてしまえばいいだろう、入れ替えの法則は俺しか知らないし…」と考えて、独自の法則でデータを暗号化しても問題なさそうです。
しかし、セキュリティ性能から見るとこの考え方は間違いです。
標準化されている暗号は世界中の研究者が攻撃方法を研究した上で生き残っているものです。それに対し、安易に作った暗号は専門の研究者に掛かればひとたまりもありません。暗号の攻撃方法は多種多様であり、色々な手法を駆使して行われます。例えば、本コースの中で触れる「サイドチャネル攻撃」は暗号処理中に発生するノイズを元に暗号鍵を見つけ出す攻撃です。
さまざまな攻撃からデータを守るためには、安全な暗号を選択することが重要です。安全な暗号は、CRYPTREC がリスト (電子政府推奨暗号リスト) を公表しているので、このリストに挙げられている暗号を使用するのがお勧めです。
但し、日々進化していく暗号に対する攻撃方法に対応して電子政府推奨暗号リストも更新されていきます。リストに挙げられていた暗号が更新時にリストから無くなることもあります。そのため、出来る限り最新の暗号を使用することが安全です。
まとめ
今回は暗号の概要として、暗号の種類や共通鍵暗号と公開鍵暗号を使用した通信を解説しました。
次回は共通鍵暗号である AES 暗号の詳細について解説します。数学が苦手な技術者にとって暗号は難しそうに思えますが、FPGA に暗号機能を実装することは意外と難しくないと思って頂けるような内容にしたいと思います。
株式会社ゴフェルテック 川西紀昭

