みなさんこんにちは。この記事は ACRi ブログの Deep Learning コースの第9回目です。
前回までの記事で、推論カーネルのタスク並列性・ループ並列性を順に抽出してきました。この記事では、推論カーネルのデータ並列性を抽出していきます。
データ並列性
データ並列性は処理対象となるデータ間の並列性を示します。
以下のコードは単純なベクトルの加算処理ですが、c[0] の計算と c[1] の計算の間には依存がないため同時に計算することができます。この並列性がデータ並列性となります。
for (int i = 0; i < N; i++) {
c[i] = a[i] + b[i];
}一方、以下のような処理の場合は、b[1] の値は b[0] に依存してしまうため、この場合はデータ並列性を抽出することができません。
for (int i = 0; i < N; i++) {
b[i+1] = a[i] + b[i];
}前回取り上げたループ並列性との違いについて補足すると、ループ並列では各処理をパイプライン実行します。このため、上述したベクトルの加算処理の処理波形は以下のようになります。
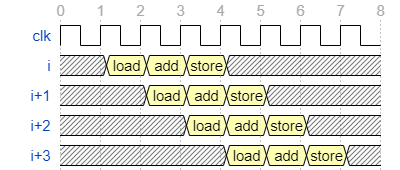
一方データ並列性を抽出することは、演算器を複製することに該当します。演算器を2つ複製した場合の波形は以下のようになります。
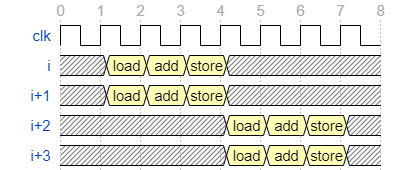
データ並列性を扱う上で難しいのは、データ並列性を抽出すればするほど、ハードウェアリソースの消費量が増えることです。特に問題になりやすいのがメモリに対するアクセスリソース (load/store) です。FPGA 内の BRAM は1サイクルあたり最大で合わせて2回までの load/store しか発行できないので、サイクルあたりに3回以上の load/store が必要な場合は BRAM が複製されるため注意が必要です (アクセス先が BRAM の場合)。
ループ並列性・データ並列性は下図のように同時に抽出可能です。
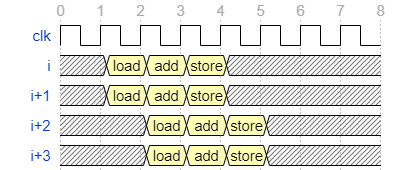
この記事で扱うコードは全て2つの並列性を同時に抽出したものとなります。
畳み込み処理におけるデータ並列性
畳み込み処理の6段ループ (出力チャネル, y 座標, x座標, 入力チャネル, カーネル y 方向, カーネル x 方向) では様々な並列性が抽出可能です。
この記事では、そのうち2つの並列性を抽出し、カーネルの性能を向上させます。
まず、一つ目に抽出可能な並列性が下図に示す処理ピクセル間の並列性です。

橙・青のピクセルの計算は互いに依存しないため、これらは同時に行うことができます。また、畳み込み計算に用いるカーネル (黄) はどちらの計算にも共有できます。このため、一回の処理 (畳み込み2回) に必要なメモリアクセスは、ピクセルを2回読み出し、カーネルを1回読み出しとなります。
二つ目の並列性は、下図に示す出力チャネル間の並列性です。
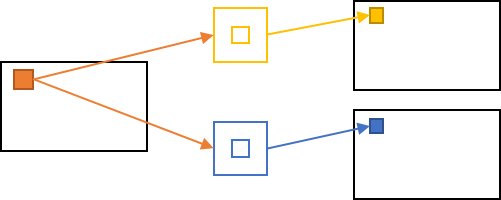
黄・青のカーネルを用いた畳み込み計算は互いに依存しないため、これらも同時に行うことができます。この例では逆にカーネルは2つ読み出しが必要なものの、ピクセルは1回の読み出しで済みます。一回の処理 (畳み込み) に必要なメモリアクセスは、ピクセルを1回読み出し、カーネルを2回読み出しとなります。
両方の並列性を図示すると下図のようになります。2つのピクセル読み出し、2つのカーネル読み出しで4つの出力値を計算できています。
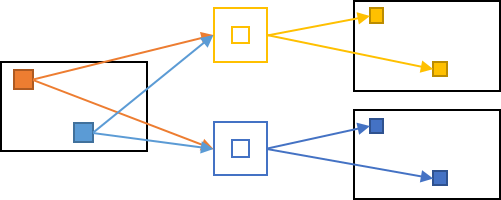
この図を元に実装する HW のブロック図を書くと以下のようになります。
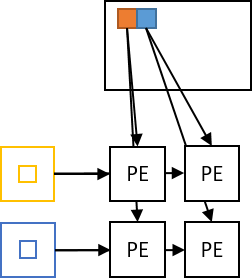
ここで重要なのが演算器 (PE) を格子状に並べることができていることです。
一つの軸 (ピクセル/出力チャネル)に対してしかデータ並列化を行わなかった際には、並列度n に対し演算器が n 個しか並びません。前述したように並列度の増加は結果として BRAM 等のメモリリソースの使用量の増加に繋がるため、FPGA 内のリソース数が総 DSP > BRAM ポート数なこともあり、一つの軸で並列化を行った場合は DSP を十分に使い切ることができません。
一方で上図のように2つの軸を並列化すると、ピクセル側の並列度を n, 出力チャネル側の並列度をmとすると、総メモリアクセスポート数としては n+m の増加量に対し、演算器はn*m 個並べることができます。このようにすると、 FPGA 内のリソースの大部分を演算に割り当てることができるようになります。xDNN など、多くの DNN アーキテクチャはこのように複数軸のデータ並列性を同時に抽出しています。
コードへの変更
2つの軸のデータ並列の仕方は全く同じなため、この記事では2つの軸を両方とも並列化した結果のみを記載します。また、前回の記事でシフトレジスタを使用して II=1 を達成しましたが、ここではその前の版を使用します。利用は後述します。
変更後の畳み込み関数は次のようになります。コード全体は GitHubリポジトリ より確認できます。
203 template <int UNROLL_X, int UNROLL_OCH>
204 static void conv2d_unrolled_v2(const float* x, const float* weight, const float* bias, int32_t width, int32_t height,
205 int32_t in_channels, int32_t out_channels, int32_t ksize, float* y) {
206
207 for (int32_t block_och = 0; block_och < out_channels; block_och += UNROLL_OCH) {
208 for (int32_t h = 0; h < height; ++h) {
209 for (int32_t block_w = 0; block_w < width; block_w += UNROLL_X) {
210 float sum[UNROLL_OCH][UNROLL_X];
211 #pragma HLS array_partition variable=sum complete dim=0
212
213 for (int32_t ich = 0; ich < in_channels; ++ich) {
214 for (int32_t kh = 0; kh < ksize; ++kh) {
215 for (int32_t kw = 0; kw < ksize; ++kw) {
216 #pragma HLS pipeline II=4
217 for (int local_och = 0; local_och < UNROLL_OCH; local_och++) {
218 #pragma HLS unroll
219 for (int local_w = 0; local_w < UNROLL_X; local_w++) {
220 #pragma HLS unroll
221 if (block_w + local_w < width && block_och + local_och < out_channels) {
222
223 int32_t och = block_och + local_och;
224 int32_t w = block_w + local_w;
...
234 float last = (ich == 0 && kh == 0 && kw == 0) ? 0 : sum[local_och][local_w];
235
236 int64_t pix_idx = (ich * height + ph) * width + pw;
237 int64_t weight_idx = ((och * in_channels + ich) * ksize + kh) * ksize + kw;
238
239 sum[local_och][local_w] = last + x[pix_idx] * weight[weight_idx];
240 }
241 }
242 }
243 }
244 }
245 }
246
247 for (int local_och = 0; local_och < UNROLL_OCH; local_och++) {
248 #pragma HLS unroll
249 for (int local_w = 0; local_w < UNROLL_X; local_w++) {
250 #pragma HLS unroll
251 if (block_w + local_w < width && block_och + local_och < out_channels) {
252 int32_t och = block_och + local_och;
253 int32_t w = block_w + local_w;
254
255 // add bias
256 y[(och * height + h) * width + w] = sum[local_och][local_w] + bias[och];
257 }
258 }
259 }
260 }
261 }
262 }
263 }主な変更点としては以下です。
- テンプレート引数
UNROLL_X, UNROLL_OCHの追加 (L203) - 出力チャネルループを2段階に変更 (L207, L217, L247)
- x方向ループを2段階に変更 (L209, L219, L249)
- 総和レジスタの複製 (L210)
- 新たなプラグマ
unrollの追加 (L218, L220, L248, L250) - 内部ループのパイプラインの II を4に設定 (L216)
1 では関数のパフォーマンスを外部から指定できるようにテンプレート引数を追加しています。Vivado HLS / Vitis では C++ のテンプレートと非常に相性がよく、今回のような使い方だけでなく#pragma HLS pipeline II=<TEMPLATE_VALUE> のような設定も可能です。Verilog HDL 等を書きなれている人からすると、ほぼモジュールの parameter 構文のように使えます。
2 で行った出力チャネルループの変更ではデータ並列化時の並列度 UNROLL_OCH だけ内側の local_och ループで回し、外側の block_och ループは UNROLL_OCH 幅でループを回します。このようにすると出力チャネル数が UNROLL_OCH の倍数でなかった際に配列の要素外アクセスが発生してしまうため、L221 のような処理が必要となります。
また、 local_och のループは元のコードで最も内側のループだった kw ループよりも内部に移動しています。この問題ではこの変更は出力結果に影響を及ぼしませんが、処理する問題によっては出力結果が変わるような依存がある場合もあるので注意が必要です。
3 は 2の修正と全く同様で、4 の 総和レジスタは上述した格子状の演算ユニット (PE) の計算結果を格納するレジスタとなります。
5 の #pragma HLS unroll は、ループに対してデータ並列を施し演算器を複数並べるためのプラグマです。デフォルトではループの反復数だけ演算器を複製しますが、これは引数 factor=N を与えることで演算器を複製する数が制御できます。
このプラグマを local_och, local_w ループの2つに設定しているため、L223-239 の総和処理及びL252-L256 のバイアス加算・出力処理は UNROLL_W * UNROLL_OCH 個だけ複製されます。L239 で行っているx, weight のロード処理も UNROLL_W * UNROLL_OCH 個だけ複製されているように見えますが、コンパイラの最適化により各ポートの増加数はそれぞれ UNROLL_W, UNROLL_OCH 個だけで済みます。
6 で設定した II=4 という値は、前回の記事で見た fadd 処理のレイテンシです。前回の記事では、シフトレジスタを使用し、以下のような波形を実装するテクニックを紹介しました。
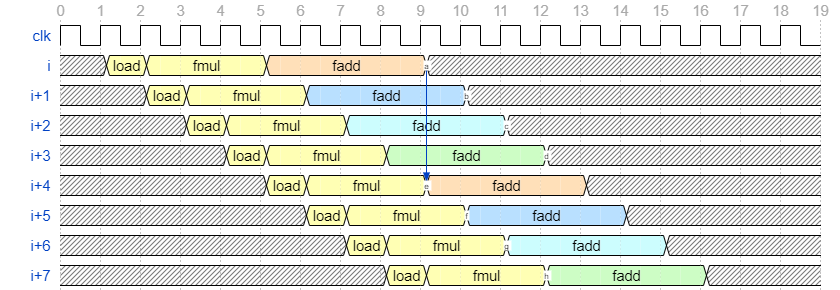
この例ではシフトレジスタを使用して出力先レジスタをサイクル毎に切り替えましたが、今回のようにデータ並列化を行っている場合は計算先となるデータをサイクル毎に切り替えるだけで済みます。左のラベルを変えただけですが、これを図示すると下図のようになります。
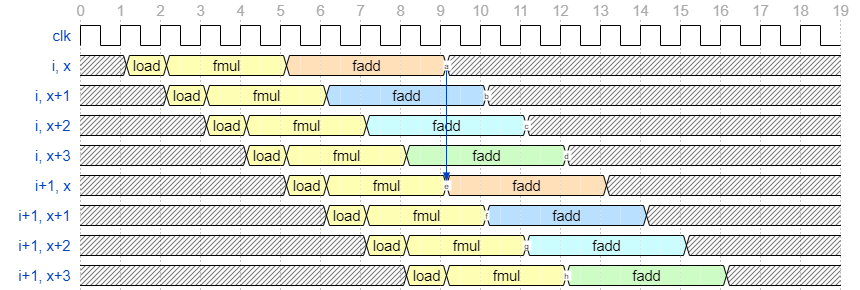
このようにすると、前回のようなシフトレジスタ間の総和も必要なくなるので効率が良いです。
また、 II=4 に設定しているもう1つの理由として、x, weight のポート数が挙げられます。これらは基本的に BRAM として実装されているため、サイクルあたり合計で2回の read/write が可能です。x は畳み込み層の処理中は畳み込み層による読み出ししか行われないため、サイクルあたり2回の read までは可能ですが、これだとデータ並列化の並列度を4としたときにポート数が不足します。
今回は II=4 のため、並列度を4としたときには4サイクル毎に4つのデータを供給すればよいです。これは 1 読み出しポートがあれば十分なため、BRAM のデフォルト帯域でも十分足ります。並列度を16 以上にしたい場合にどうするべきかについて軽く説明しておくと、これは #pragma HLS array_partition というプラグマにより実現可能です。以下に UG902 内の図を添付します。
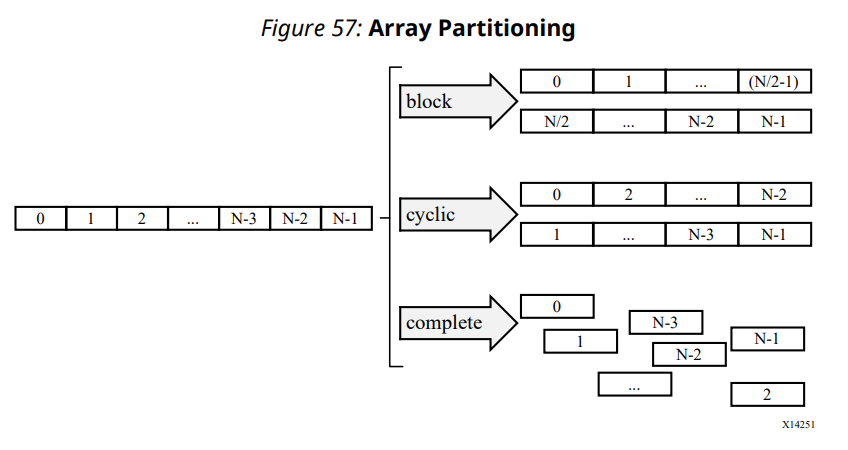
C 内で定義した配列はデフォルトでは図中左のような1ポートの配列となります。これをどのように実装するかをこのプラグマで設定可能で、前回/今回の記事でも使用したようにレジスタとして展開する場合は complete を使用し、今回のlocal_x ループのように、x, x+1 を同時にアクセスする場合は cyclic が使えます。本当は II を下げずにこのプラグマを適切に設定するのが王道ではあるのですが、このプラグマは配列リソースの定義スコープ (今回は inference 関数) に定義しなければならず、変更に手間がかかるため今回は使用しませんでした。
合成結果・パフォーマンス
x 方向の並列度を4、出力チャネル方向の並列度を4 の畳み込み関数を使用し、推論関数を合成しました。この畳み込み関数は前述したように II=4 となるため、4サイクルにつき16回の演算を行います。この構成では必要な演算器数は 16/4 = 4 となり、各メモリへのアクセスポートは 4/4 = 1 ポートとなります。
高位合成結果を確認してみると、畳み込み関数内の浮動小数点演算器リソースの使用量は次のように変化しています。
元の構成だと fadd が2つ、 fmul が1つで、2つの fadd のうち full_dsp_1 となっている方はバイアスの加算に用いられます。それに対しデータ並列後の結果では fadd が6つ、 fmulが4つとなり、バイアス加算に用いる full_dsp_1 が2つに増えていること以外は、 fadd/fmul が各4つで想定通りのリソース量となっていることが分かります。
パフォーマンスレポートは以下のようになり、前回記事時点で 0.423 ms だった conv2 の実行時間が、82.875 us まで高速化できています。
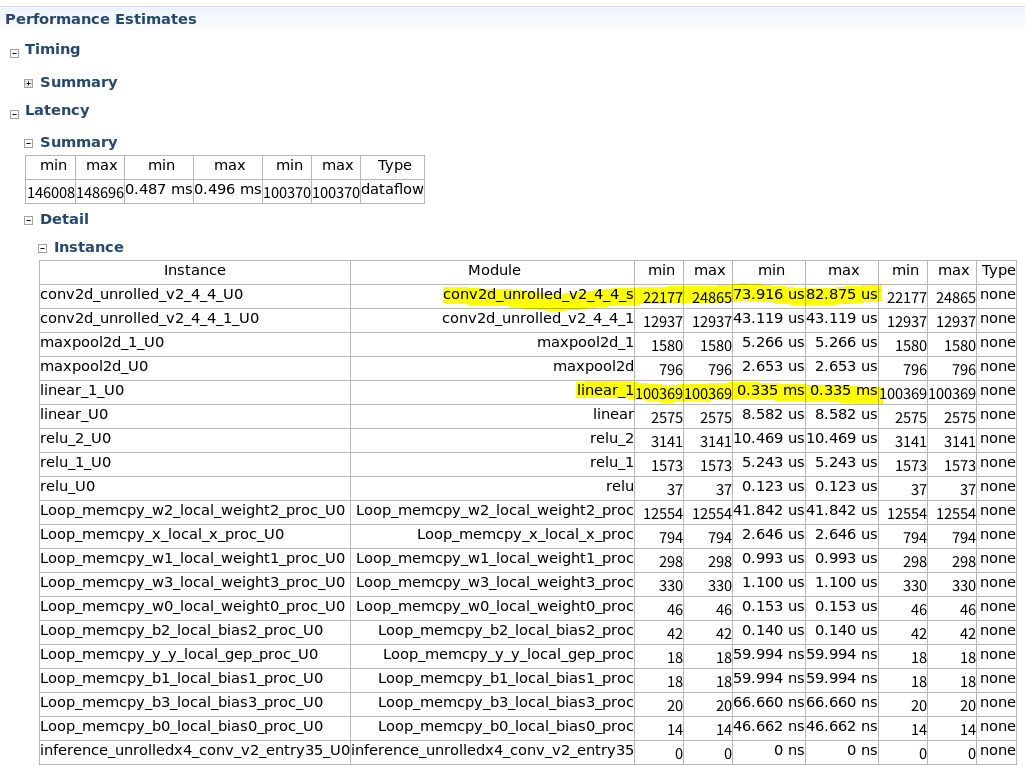
この構成では、既にボトルネックは全結合層の 0.335 ms となります。
実機での実行結果は以下のようになり、これを見ても全結合層の実行時間が1フレームの処理時間となっています。
$ ./host/run_inference ./host/inference_unrolledx4_conv_v2_hw.xclbin inference_unrolledx4_conv_v2 1
Elapsed time: 0.335922 [ms/image]
accuracy: 0.973全結合層に対するループ・データ並列化も含めた最終版
上記のカーネルでは全結合層がボトルネックとなっていたため、全結合層にも最適化を施した版を実装しました。コードはここには貼らないので、コードリポジトリ上の linear.h をご確認ください。全結合層はベクトルと行列の積のため、畳み込み層のように2軸に対するデータ並列化はできない点は異なりますが、基本的に畳み込み層と同じ手順で最適化を行えます。
第7回の記事で示したように、タスク並列を最も効率よく行えるのはタスク間の処理時間が均一になる場合です。これを目標としてパラメータチューニングを行った最終版の conv1, conv2, fc1, fc2 の 並列化度及び実行サイクル数が以下の表になります。元々圧倒的に処理が軽かった fc2 は低いままですが、他のカーネルは概ねバランスが取れるようになりました。
| 層 | 並列化度 (出力チャネル) | 並列化度 (x方向) | 実行サイクル数 | 実行時間 (us) |
|---|---|---|---|---|
| conv1 | 4 | 4 | 12741 | 42.466 |
| conv2 | 4 | 8 | 12937 | 43.119 |
| fc1 | 4 | – | 12721 | 43.399 |
| fc2 | 1 | – | 383 | 1.277 |
実行性能
これを実機で実行すると、次のようになりました。実行時間は 49 us まで短縮され、元々は 20.81 ms かかっていた最初の実装と比べると圧倒的に速くなっています。
$ ./host/run_inference ./host/inference_final_hw.xclbin inference_final_v2 1
Elapsed time: 0.049805 [ms/image]
accuracy: 0.973全体の高速化結果
第7回から3回の記事をかけて、推論カーネルにタスク並列化・ループ並列化・データ並列化を行ってきました。これらによる最適化結果をまとめると、以下の表のようになります。
| 名称 | 実行時間 (ms/image) | 直前の実装からの速度向上率 | ベースラインからの向上率 |
|---|---|---|---|
| ベースライン | 20.81 | 1.00 | 1.00 |
| タスク並列化 | 12.65 | 1.65 | 1.65 |
| ローカルバッファによる外部メモリアクセス削減 | 1.61 | 7.86 | 12.93 |
| ループ並列化 (畳み込み層のみ) | 0.61 | 2.64 | 34.11 |
| データ並列化 4×4 (畳み込み層のみ) | 0.336 | 1.81 | 61.93 |
| 最終版 | 0.0498 | 6.75 | 417.87 |
またこれまでの記事では取り上げませんでしたが、各最適化結果あたりのリソース使用量は次のようになります。末尾の行は、U200 の一つの SLR 内の使用可能なリソース量です。
| 名称 | BRAM_18K | DSP48E | FF | LUT |
|---|---|---|---|---|
| ベースライン | 49 | 20 | 13592 | 15600 |
| タスク並列化 | 61 | 20 | 13785 | 15955 |
| ローカルバッファによる外部メモリアクセス削減 | 84 | 21 | 13800 | 16967 |
| ループ並列化 (畳み込み層のみ) | 84 | 21 | 15363 | 18653 |
| データ並列化 4×4 (畳み込み層のみ) | 86 | 43 | 22335 | 27020 |
| 最終版 | 90 | 63 | 32764 | 33674 |
| U200 (per SLR) | 1440 | 2280 | 788160 | 394080 |
まず実行性能についてみていくと、これらのチューニングにより最終的にベースラインの 417.87 倍の速度が出るようになりました。特に効果が大きかったのはローカルバッファによる外部メモリアクセス削減、最終版 (全結合層の高速化 + 層間のバランス) の2つです。この2つは前者は大きな RAM リソースの増加、後者は演算器リソース (DSP, LUT) の増加が必要となっていますが、その分大きな速度向上を得られています。
また、400倍以上の性能向上を達成しているのに対し、リソース増加量でみると最も増加率の高い DSP ですら 63 / 20 = 3.15 倍で済んでいます。特にタスク並列化・ループ並列化はほとんどリソース増加を伴わずに性能を向上させることができているため非常に好ましい結果です。
現状のカーネルでも FPGA 内部のリソースはまだまだ余っているので、更なる最適化は十分に適用可能です。今回のようにカーネル内のデータ並列性を更に抽出することもできますし、またカーネル自体を複製してフレーム間の並列性を取ることも可能です。特に前者だけを行っていくと合成時のタイミング制約を満たしにくくなっていくので、どこかのタイミングで後者のアプローチをとることになると思います。カーネル複製のやり方に興味があれば、以下の記事が分かりやすいのでお勧めです。
まとめ
今回ターゲットとした MNIST というデータセットは画像サイズが 28×28 の非常に小さなデータセットです。また今回のモデルは非常に軽量なネットワークモデルです。これらをより現実的なデータ・モデルにすると次のように演算規模が変化します。
- 解像度: 28×28 -> 幅、高さ共に数百~数千
- ネットワーク規模: 2層 (畳み込み層換算) -> 数十~数百
現実的なモデルで求められる計算量を雑に計算すると、今回作成したネットワークモデルの 1,000~1,000,000 倍程度必要となります。これが1000倍程度なら現在配置している演算器数のままでも数十ms オーダで処理できますが、これ以上増えていくと 60fps 等のリアルタイムな画像処理は難しくなってきます。このため、実際は量子化、枝刈り という計算コストを減らすための手法が用いられます。最終回となる次回の記事ではこれらについて説明していきます。
このブログに記載しているコードは https://github.com/fixstars/dnn-kernel-fpga で公開しています。コードの権利、ライセンスに関してはライセンスファイルを参照して下さい。
株式会社フィックスターズ シニアエンジニア 松田裕貴



