みなさんこんにちは。このコースでは FPGA を使いこなすために理解しておきたい論理回路の基本について説明します。FPGA を使って開発しているけどハードウェアはよく分からないという方は、ぜひお付き合いください。
前回までの記事で、クロック同期回路を理解するための論理回路の基礎を説明してきました。今回は、4ビットカウンタ回路を例にクロック同期回路の設計を説明します。
4ビットカウンタ回路の設計
仕様
4 ビットカウンタは 0 から 15 (16 進数で 0x0 から 0xF) までを数える回路です。この記事で設計する 4 ビットカウンタ回路の仕様は次の通りです。
入力:クロック(CLK)とリセット(RST) 出力:カウンタの値(COUNT、4ビット) 挙動:クロックの立ち上がりでカウンタの値を1増加、 リセットが1の時はクロックとは無関係にカウンタの値を0にする。
この回路では、カウンタの値がフリップフロップに保持されます。前回の記事で紹介したフリップフロップの入力はクロックと入力値だけでしたが、さらにリセット信号も入力とするフリップフロップもあります。そのようなフリップフロップはリセットがかかると値が 0 (電圧が低い状態) にセットされます。論理回路を設計するとき、最初にフリップフロップの値を初期化することが多く。今回のようにクロックとは無関係にフリップフロップの値をリセットすることを非同期リセットと呼びます。
設計する4ビットカウンタ回路のブロック図を次に表します。ブロック図は、回路を機能ごとに抽象的に表現した図です。
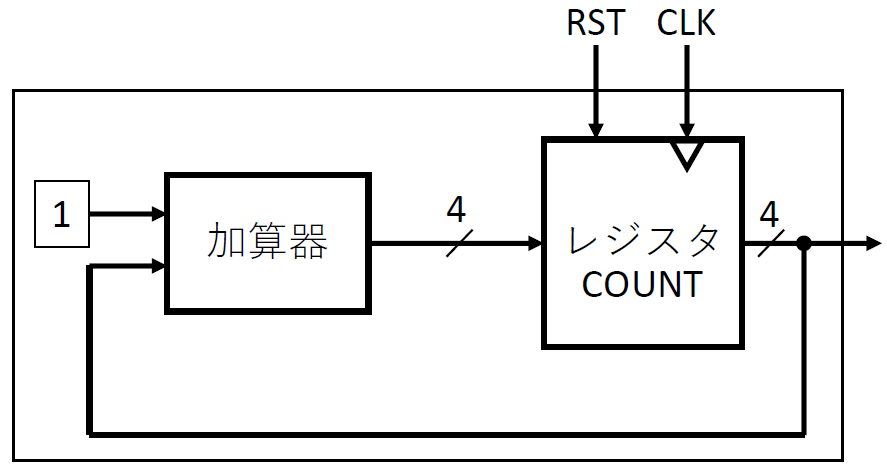
入力の CLK と RST は1ビットです。出力の COUNT は4ビットです。
SystemVerilog 記述
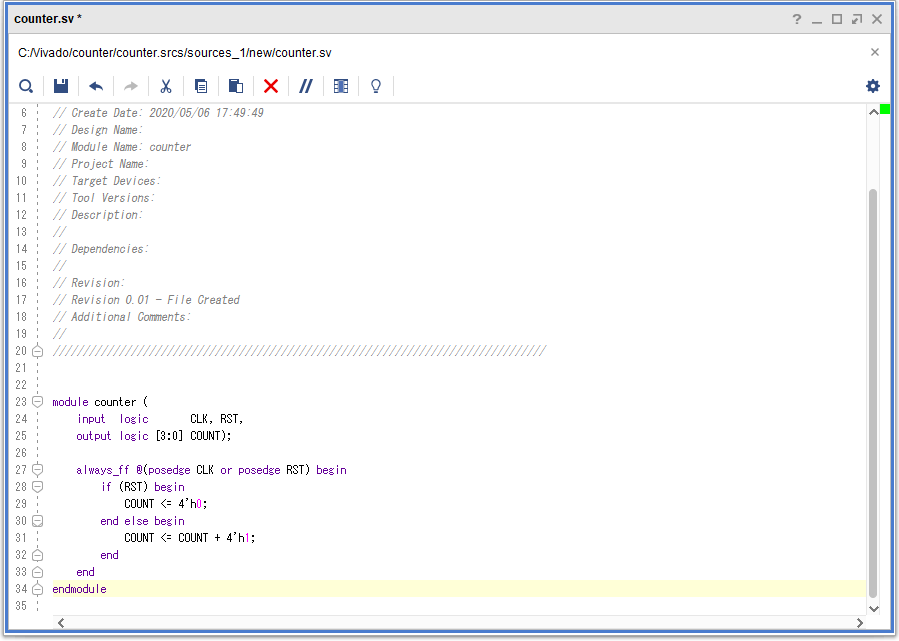
この回路を SystemVerilog で記述すると下のようになります。
module counter (
input logic CLK, RST,
output logic [3:0] COUNT);
always_ff @(posedge CLK or posedge RST) begin
if (RST) begin
COUNT <= 4'h0;
end else begin
COUNT <= COUNT + 4'h1;
end
end
endmodule先頭の module から末尾の endmodule までが回路の定義です。
最初の3行は宣言です。1 行目で module 名を counter としています。2 行目は入力のinput logic として、CLK と RST の2つを定義します。信号のビット幅を指定しない場合は 1 ビットになります。3 行目は出力の output logic で、COUNT を定義します。信号のビット幅は 4 ビットで、[3:0] と宣言しています。このように宣言すると 4 ビットの下位から順に COUNT[0]、COUNT[1]、COUNT[2]、COUNT[3] となります。
5行目から11行目までの always_ff のブロックでカウンタ回路の挙動を記述します。クロックの立ち上がりでカウンタ値を +1 し、リセットが1の時にカウンタ値を0にセットします。always_ff 文は順序回路を記述します。
「@」の後にはブロック内の文が処理されるタイミングを立ち上がり (posedge) または立ち下がり (negedge) で指定します。「posedge CLK」と「posedge RST」はそれぞれ CLK と RST の立ち上がりを指定しています。「posedge CLK or posedge RST」とするとCLK の立ち上がりか RST の立ち上がりのタイミングでこの always_ff 文が処理されます。CLK の立ち上がりでカウンタ値を +1 するために posedge CLK が必要です。RST が1になった時 (0 から 1 に変わる瞬間) にカウンタ値を0にリセットするために posedge RST が必要です。
続く if 文では、RST が1の時は COUNT に0を代入し、それ以外の時は COUNT にCOUNT + 1 を代入しています。「4’h0」と「4’h1」は定数を表現していて、それぞれが4ビットの16進数 (Hexadecimal) で0と1です。ここでは、代入の演算子として「<=」を使います。これはノン・ブロッキング代入と呼ばれる代入文です。
もうひとつの代入の演算子として「=」があります。こちらはブロッキング代入と呼ばれます。例えば、いま a の値を0、 b の値を1とします。「a = 2」という文に続いて「b = a」という文があると、値の代入操作は文が処理された瞬間に行われて a の値は2になり、次の「b = a」で b の値も2になります。
前者のノン・ブロッキング代入では「@」で指定されたタイミングで代入操作が行われます。同じように a の値を0、 b の値を1とします。「a <= 2」に続いて「b <= a」という文があると、値の代入操作は指定されたタイミングに同時に行われるので、 a の値は2になり b の値は 0 (元の a の値) になります。
別の例として、ソートアルゴリズムなどで使う2つの変数 a と b の値のスワップは、ブロッキング代入ではもう一つ変数を使って「tmp = a、a = b、b = tmp」のように記述する必要があります。一方、ノン・ブロッキング代入では「a <= b、b <= a」と記述できます。
Vivado で論理合成
4ビットカウンタ回路を記述したので、さっそくシミュレーションで挙動を確認したいところですが、シミュレーションにはテスト用のコードが必要になるので次回に説明します。今回は、設計したカウンタ回路がどのようなハードウェアになるのかを論理合成によって確かめてみます。
実際に FPGA で設計するときはシミュレーションで実装したコードが想定通りの挙動になるか検証してから論理合成をするのが普通なので、今回のようにいきなり論理合成はおこないません。論理合成はそれなりに時間がかかる重い処理のため、シミュレーションでの検証が重要です。
まずは「Vivado のインストールと使いかた」の記事を参考に Vivado を使う環境を用意してください。
Vivado を起動して「Create Project」から新しいプロジェクトを作成します。次に「Project name」を「counter」、「Project location」を適当なフォルダに設定して次に進みます。
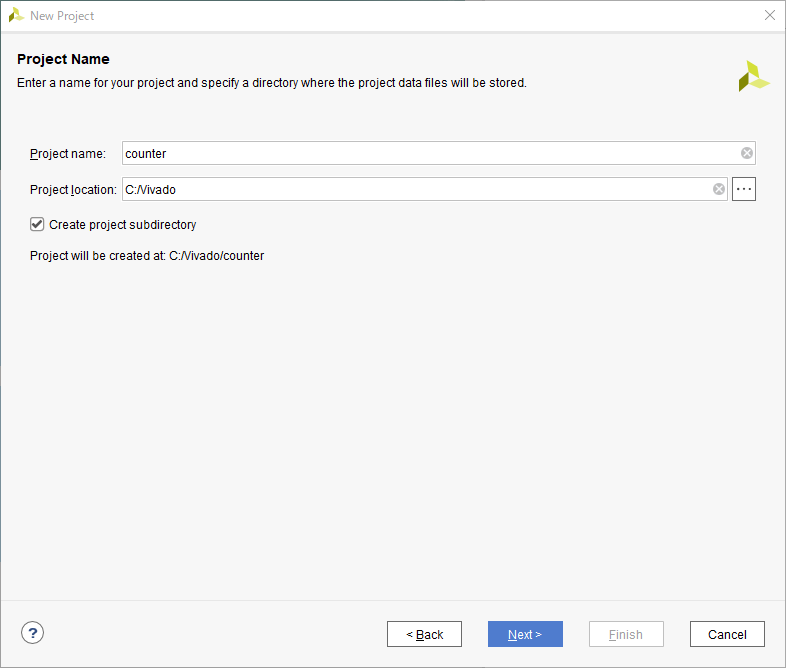
「Project Type」では「RTL Project」を選択して次に進みます。
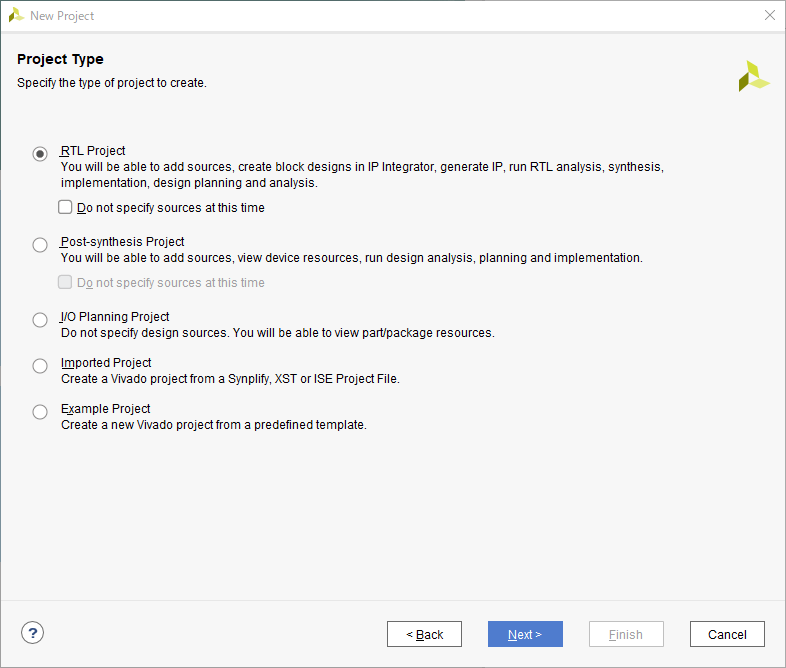
「Add Sources」で「Create File」をクリックし、「File type」を「SystemVerilog」、「File name」を「counter.sv」とします。「File location」はそのままで OK です。
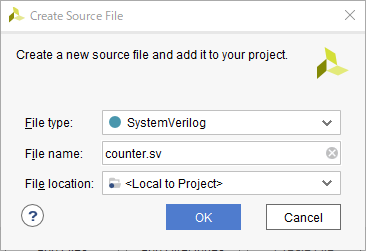
「Add Constraints」では、今回は制約ファイルは使わないのでそのまま次に進みます。実際に FPGA で回路を動かす際には制約ファイルが必要になります。
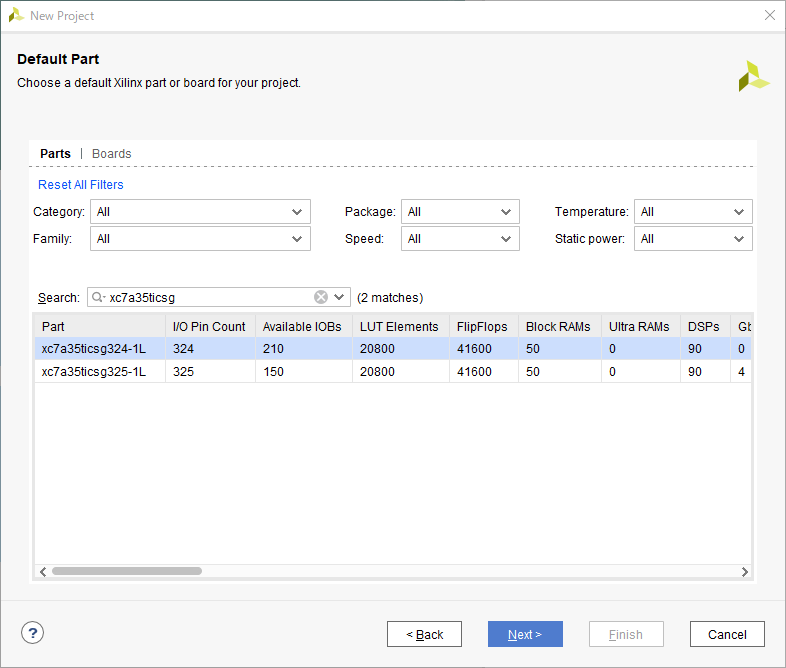
「Default Part」ではFPGA の型番を選んびます。「xc7a35ticsg324-1L」を選択しましょう。この FPGA は「シリアル通信で Hello, FPGA」の記事で使われているものと同じです。
プロジェクトを生成します。「Define Module」はそのままで「OK」します。
赤丸で示した「Sources」のcounterをダブルクリックして開き、4ビットカウンタの SystemVerilog のコードをコピー&ペーストして保存します。
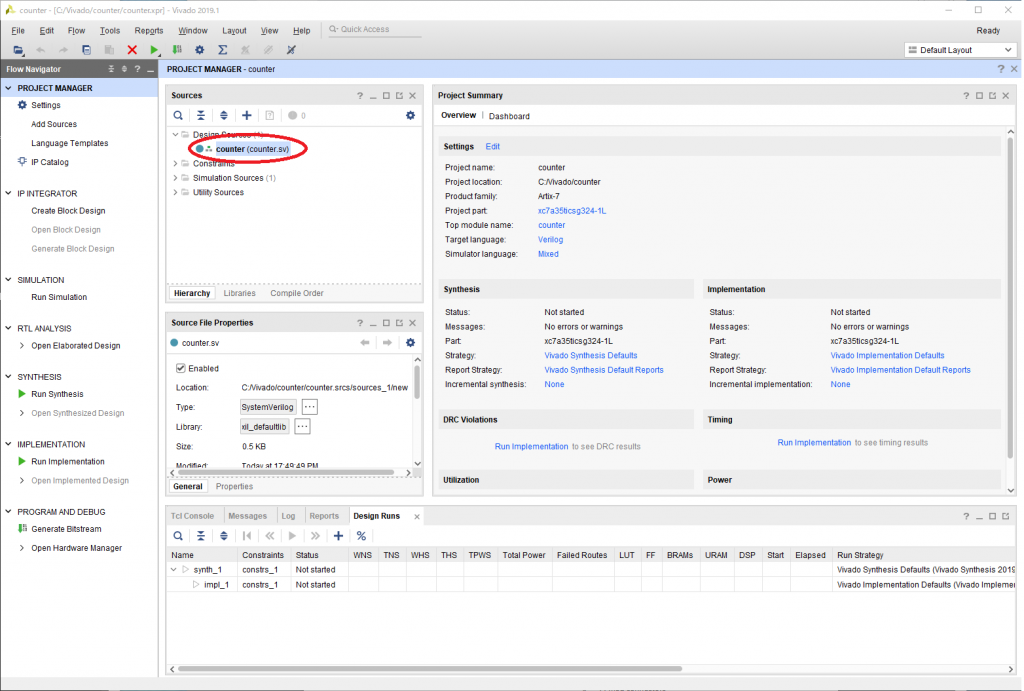
次に、赤丸で示した「Run Synthesis」をクリックして、論理合成を実行します。
「Synthesis successfully completed.」と出たら論理合成は終了です。「Open Synthesized Design」を選択して「OK」します。
生成された回路を確認するには、赤丸で示した「Schematic」をクリックします。
下の図のような回路図が表示されます。
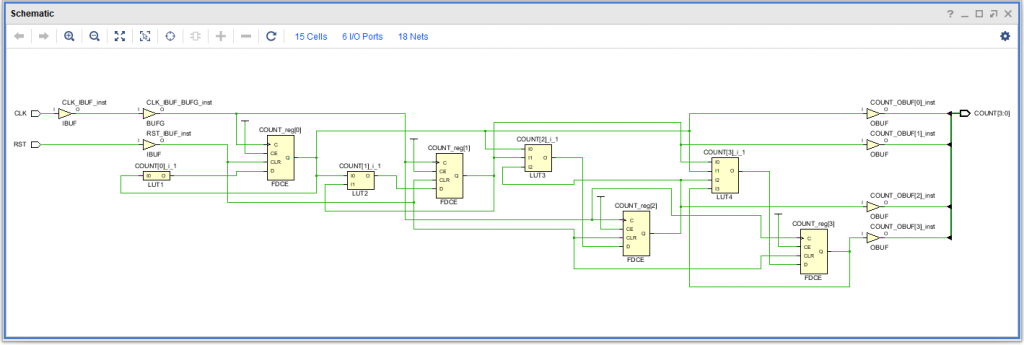
縦長の大きい四角で表現されている COUNT_reg[0] から COUNT_reg[3] までが4つのフリップフロップです。また、それぞれのフリップフロップへの入力となる LUT1 から LUT4 という4つのルックアップ・テーブルを確認できます。最初のブロック図では +1 する回路を「加算器」として描きましたが、一般的な全加算器よりも最適化された回路が作られています。
図の左端と右端にある三角形のシンボルで表現されている論理回路はバッファとよばれます。入力をそのまま出力するもので、何の役にたつのか不思議に思うかもしれませんが、重要な回路です。本題から離れてしまうのでこの記事では詳細は説明しません。
回路図の左端の四角で表現されている LUT1 を右クリックし「Cell Properties」見てみましょう。赤丸で示した「Truth Table」をクリックすると、ルックアップ・テーブルによって実現されている真理値表が確認できます。
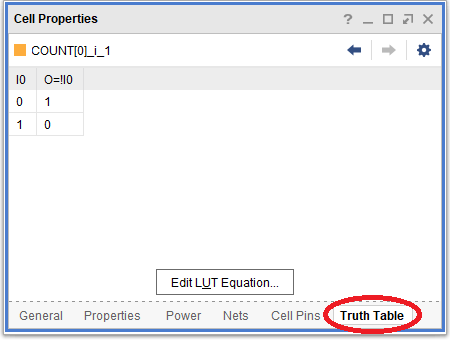
実は LUT1 は NOT 回路として用いられています。カウンタの最下位ビットは毎クロック0と1 を繰り返すだけなので 、よく見ると、4ビットカウンタの最下位ビットの COUNT_reg[0] の出力を LUT1 で実現される NOT で反転した値が、同じフリップフロップの入力になっています。
ほかの LUT についても確認してみます。この4ビットカウンタ回路は論理ゲートで表現すると下の図となります。
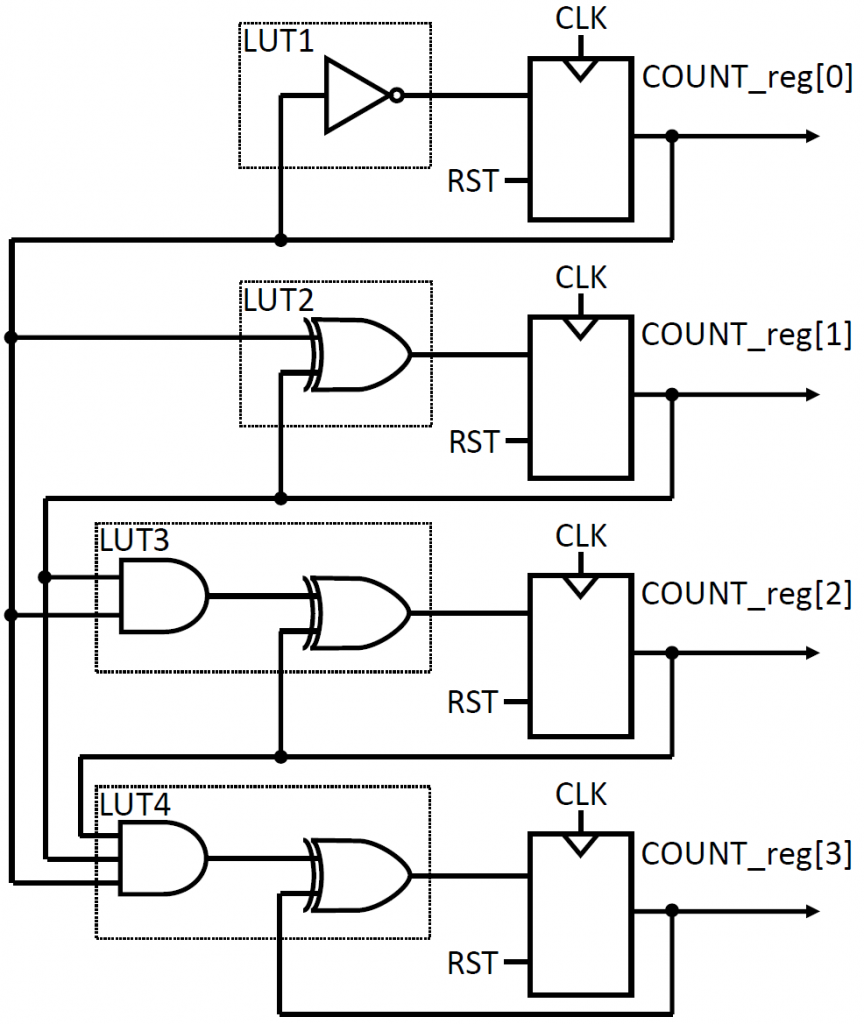
カウンタ値の 2 ビット目(COUNT_reg[1])から 4 ビット目(COUNT_reg[3])では、AND ゲートで下位のビットからの桁上がりを計算し、XOR ゲートで現在の値との和を計算しています。LUT4 におけるANDゲートが3入力である点には注意してください。
実際に論理合成をしてみると、カウンタ回路は複数の全加算器を使うよりもシンプルな回路になっています。論理合成ツールによる最適化は優秀で、設計者が考えていたよりもシンプルな回路になることがあります。
FPGA を使った開発ではより複雑な回路を設計することになります。仕様を考えたときにフリップフロップになる部分と組み合わせ回路になる部分をイメージすることが大切です。(組み合わせ回路の具体的な構成は論理合成ツールにまかせればよいですが。)
まとめ
今回は、4 ビットカウンタ回路の設計について、SystemVerilog の記述と論理合成で生成される回路を確認しました。
次回は設計した4ビットカウンタのテストコードを記述して、挙動を確認していきます。自分で設計したコードがハードウェアとして動く様子が実感できます。お楽しみに。
東工大 佐藤真平