この連載では、 FPGA の応用事例として、「組合せ問題」を高速に解く試みについて触れていきます。 FPGA のアプリケーションとしては、画像処理や深層学習 (いわゆるAI) などが有名ですが、組合せ問題を FPGA で高速に解こうという試みは FPGA 研究の比較的早い時期 (90年代末) に起こり、今日に至っています。
この連載では、組合せ問題の定義や用途、組合せ問題を解くためのアルゴリズム、その FPGA を用いた高速化に関して、実装例などを交えて紹介します。なお、初回は FPGA に関してはあまり触れませんが、悪しからずご了承ください。
組合せ問題とは
ひと言で言うと、その答えが離散的 (飛び飛び) な数量の組合せで表現される問題のことです。
特に、数ある答えの中から最も優れたもの (最適解) を探す問題を「最適化問題」といいます。これに対して、「答えとなる組合せがあるかないかを判定する問題」を「決定問題」といいます。前者の代表例としては巡回セールスマン問題、後者の代表例としては充足可能性問題などが挙げられます。なお、単に「最適化問題」とか「決定問題」と言っただけでは、必ずしも離散的な数量ばかりを扱うわけではないのですが、この連載ではそこまでは考えません。
具体例
その1 充足可能性問題
充足可能性問題は、和積形論理式に含まれる全ての節が真になるような論理変数への割当 (充足解) が存在するかどうかを判定する決定問題です。充足解が1つでも存在する場合を「充足可能」、充足解が存在しない場合を「充足不能」といいます。以下、図1 を例に説明します。

論理変数 x1 〜 x3 とその否定をリテラル、 C1〜 C3のように、リテラルの論理和の形をしている論理式を節といいます。また、節の論理積をとったものを和積形論理式といいます。この例題は、(x1, x2, x3) = (1, 0, 1) のとき、全ての節が真になるため、充足可能ということになります。
充足可能性問題を英語で Satisfiability (あるいは Satisfiability Problem) と言い、その頭3文字を取って SAT と略されることから、これ以降、SATと表記します。SAT の応用としては、ハードウェアやソフトウェアの等価性検証といった工学的なものから、数独ソルバーなど、パズル的なものまで様々です。
SAT の応用例: 論理回路の等価性検証
論理回路の等価性検証、つまり、2つの論理回路が同じ入力真理値に対して必ず同じ出力を返すか、は、次のようにして充足可能性問題に変換することができます。
n 入力の論理回路 F と G への入力を (x1, x2, …, xn)、 F と G からの出力をそれぞれ f, g と置きます。 F と G が同じ入力に対して同じ出力となるかどうかは、 f と g の排他的論理和 h が0となるかどうか (図2) を調べれば分かります。
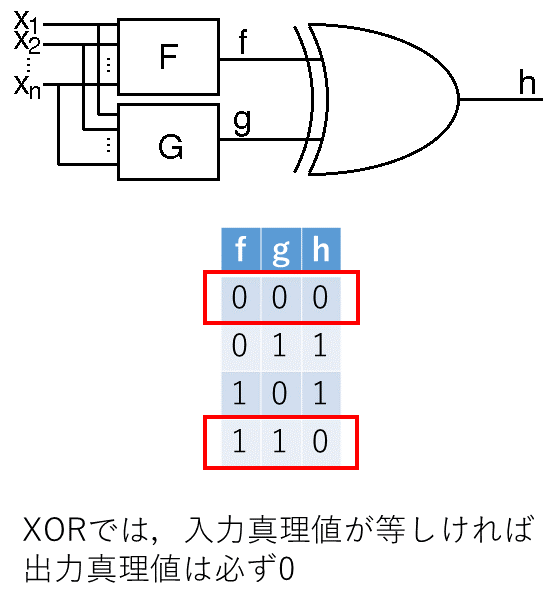
以上のことから、論理回路 F と G が等価であれば、 f, g, h に関して以下の命題がともに成り立ちます。
- 命題1: h は f と g の排他的論理和である。
- 命題2: h は常に0である。
これらを論理式で表すと、それぞれ、
- 命題1: h ⇔ f ⊕ g
- 命題2: h ⇔ 0
となります。ここで ⇔ は同値を、⊕は排他的論理和を表します。
命題1は、命題論理の法則を用いて、次のようにして和積形論理式に変形されます。
h ⇔ f ⊕ g
= (h ⇒ f ⊕ g) (f ⊕ g ⇒ h) ∵ ⇔ の定義
= (¬h ∨ ¬fg ∨ f¬g) (fg ∨ ¬f¬g ∨ h) ∵ ⇒ (ならば) の定義と排他的論理和の定義
= (¬h ∨ (¬f ∨ ¬g) (f ∨ g)) ((¬f ∨ g) (f ∨ ¬g) ∨ h) ∵二重否定とド・モルガン律
= (¬h ∨ ¬f ∨ ¬g) (¬h ∨ f ∨ g) (h ∨ ¬f ∨ g) (h ∨ f ∨ ¬g) ∵分配律
続いて命題2の式変形を行います。
h ⇔ 0
= (h ⇒ 0) (0 ⇒ h)
= (¬h ∨ 0) (1 ∨ h) = ¬h
ここで、 F と G の和積形論理式をそれぞれ C(F)、 C(G) で表し、命題1、命題2、 C(F)、 C(G) の論理積を取ったものを命題3と置きます。
- 命題3: ¬h (¬h ∨ ¬f ∨ ¬g) (¬h ∨ f ∨ g) (h ∨ ¬f ∨ g) (h ∨ f ∨ ¬g) ∧ C(F) ∧ C(G)
命題3がどんな場合でも充足すれば回路 F と G は等価、充足しない真理値割当があれば等価ではないことになります。
さらに、命題2を「 h ⇔ 1 (hは常に1である) 」という命題に置き換えると、命題3は以下のようになります。
- 命題3′ : h (¬h ∨ ¬f ∨ ¬g) (¬h ∨ f ∨ g) (h ∨ ¬f ∨ g) (h ∨ f ∨ ¬g) ∧ C(F) ∧ C(G)
命題3′ が「充足不能」なら F と G は等価、「充足可能」なら不等価となります。これで論理回路の等価性検証が充足可能性問題に変換されました。
なお、回路が和積形論理式で与えられていない場合、それを和積形論理式に変形する必要があります。ここでは、2入力 NAND の和積形論理式の導き方を示します (3入力以上の場合も同様です)。
2入力 NAND の入力を a, b、出力を c とするとき、入出力の真理値に関して以下の命題が成り立ちます。
- 命題4: c が0 ⇔ ab が1
これを論理式で表し、変形すると、以下のようになります。
命題4
= ¬c ⇔ ab
= (c ∨ ab) (¬(ab) ∨ ¬c)
= (c ∨ a) (c ∨ b) (¬(ab) ∨ ¬c) ∵分配律
= (c ∨ a) (c ∨ b) (¬a ∨ ¬b ∨ ¬c) ∵ド・モルガン律
回路が複数の論理ゲートで構成されている場合は、個々の論理ゲートをそれぞれ和積形に変形し、全ての節の論理積を取れば、回路全体の和積形論理式となります。
その2 最大充足可能性問題 (MaxSAT)
SAT は、充足するかしないかを判別する問題でしたが、与えられた例題が充足不能な場合に幾つまでなら節を充足させることができるのかを知りたいことがあり、これを考える問題を MaxSAT と言います。
これは、言わば充足節の数を最大化させる SAT であり、決定問題であった SAT を最適化問題に拡張したものです。決定問題の多くが SAT に変換可能なように、最適化問題の多くも MaxSAT に変換することができます。具体例は次回ご紹介します。
なぜ高速化するのか
SAT の充足可能性を厳密に判定するためには、基本的には全数探索、すなわち、論理変数への真理値割当を全て列挙し、それぞれ充足するかしないかを調べる必要があるのですが、これには天文学的な時間がかかってしまいます。その理由は、論理変数の数が n 個のとき、真理値の割り当て方が全部で 2n 通りもあるためです (現在は無駄な探索を省略するための手法が多数提案されていて[1]、厳密に判定できるケースも増えています) 。
他の多くの決定問題も同様の性質を持っているため、その解を求めるためには非常に時間がかかります。一方で、もし SAT が高速に解ければ、様々な決定問題を SAT に変換することで速く解けるようになることが期待できます。
MaxSAT に関しても同様で、その解を高速に求めることができれば、様々な最適化問題を MaxSAT に置き換えて高速に解くことができるようになるはずです。
このように、その波及効果の高さから、 SAT や MaxSAT を高速に解くことが望まれています。
FPGA による研究事例
SAT に対する初期の FPGA 研究の事例は文献[2]で、より新しい事例は文献[3]で、それぞれ詳しく調査されています。また、SAT そのものに関しては、2010年1月発行の人工知能学会誌第25巻1号[1]において網羅的に解説されています。MaxSAT の高速化に関しては筆者らによる事例[4]などがあります。これは、最適化問題のひとつである最大クリーク問題を MaxSAT に置き換えて FPGA で高速に解くというものです。その他、巡回セールスマン問題の高速解法[5]や、 N-queen 問題の高速解法[6]、最大カット問題の高速解法[7]などが提案されています。
まとめ
今回は、FPGA の応用事例のひとつである「組合せ問題」と、その代表例である SAT, MaxSAT について述べました。
次回以降、文献[4]を題材に、最適化問題のひとつである最大クリーク問題の MaxSAT への変換、MaxSAT を解くアルゴリズム、FPGA による高速化について触れていきます。
筑波大学 金澤 健治
参考文献
- [1] 人工知能学会誌 25 (1), 2010
- [2] Skliarova, I., & de Brito Ferrari, A, “Reconfigurable hardware SAT solvers: A survey of systems.” IEEE Transactions on Computers, 53(11), pp.1449-1461, 2004.
- [3] Sohanghpurwala, A. A., Hassan, M. W., & Athanas, P, “Hardware accelerated SAT solvers—a survey,” Journal of Parallel and Distributed Computing, 106, pp. 170-184, 2017.
- [4] Kanazawa, K., & Cai, S., “FPGA acceleration to solve maximum clique problems encoded into partial MaxSAT,” IEEE 12th International Symposium on Embedded Multicore/Many-core Systems-on-Chip, pp. 217-224, 2018.
- [5] Mavroidis, I., Papaefstathiou, I., & Pnevmatikatos, D., “A fast FPGA-Based 2-opt solver for small-scale Euclidean traveling salesman problem,” 15th Annual IEEE Symposium on Field-Programmable Custom Computing Machines, pp. 13-22, 2007.
- [6] Azuma, Y., Sakagami, H., & Kise, K., “An Efficient Parallel Hardware Scheme for Solving the N-Queens Problem,” IEEE 12th International Symposium on Embedded Multicore/Many-core Systems-on-Chip, pp. 16-22, 2018.
- [7] Zou, Y., & Lin, M., “Massively Simulating Adiabatic Bifurcations with FPGA to Solve Combinatorial Optimization,” The 2020 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, pp. 65-75, 2020.