前回は、 FPGA のアプリケーションのひとつに「決定問題」や「最適化問題」などの「組合せ問題」があること、決定問題の代表例である SAT、 SAT を最適化問題に拡張した MaxSAT について述べ、また、 FPGA による組合せ問題の高速計算に関する文献を幾つか紹介しました。
今回から、筆者らの事例[1]を題材に、組合せ問題の FPGA による高速計算について触れていきたいと思います。前回も述べましたが、これは、グラフ理論の最大クリーク問題を MaxSAT に置き換え、 FPGA 上で高速化された MaxSAT 向けソルバーを用いて解く、というものです。
まず、最大クリーク問題の MaxSAT への変換方法と、文献[1]で用いた MaxSAT の解法アルゴリズムについて述べていきます。
MaxSAT
最初に MaxSAT に関して簡単におさらいしておきたいと思います。和積形論理式 F(x1, x2, …, xn) における全ての節を充足させるような論理変数への真理値割当があるかどうかを考える問題を SAT、全ての節のうち、どのくらい多くの節を充足させることができるかを考える問題を MaxSAT と言うのでした。
Partial MaxSAT
ところで、文献[1]のタイトルを見ると、 “MaxSAT” の前に “partial” という単語が付いていることに気がついたと思います。実は、 MaxSAT には幾つかのバリエーションがあり[2-3]、筆者らが文献[1]で取り扱ったのは、そのうちのひとつである Partial MaxSAT というものです。
Partial MaxSAT は、必ず充足させなければならない hard 節と、必須ではないが充足させることが望ましい soft 節から構成されている MaxSAT で、hard節を全て充足させたうえで可能な限り多くの soft 節を充足させる解を見つけることを目的としています。
最大クリーク問題
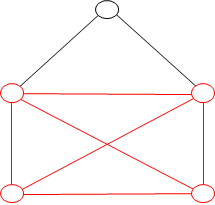
最大クリーク問題とは、無向グラフのサブグラフであって完全グラフであるもの (クリーク) のうち、最も頂点数が多いものを探す問題で、遺伝子情報処理における蛋白質立体構造アライメントなどの応用があります。完全グラフとは任意の頂点間にエッジが張られているグラフのことです。エッジが張られていることを「隣接している」といいます。図1に最大クリークの例を示します。
最大クリーク問題の Partial MaxSAT への変換
図1のグラフから Partial MaxSAT の例題を生成する方法を説明します。まず、図2のように各頂点に論理変数を割り当てます。このとき、論理変数の真理値が真のとき、対応する頂点はクリークの構成要素であり、偽のときはそうではない、と約束します。
クリークの定義から、隣接していない頂点同士は同時にクリークの構成要素になることはできません。したがって、 ある論理変数 xi が真ならば、それと隣接していない頂点を表す論理変数 xj は偽でなければなりません。なお、その逆は必ずしも成り立ちません。従って、以下の命題が成り立ちます。
命題1: xi ⇒ ¬xj
= ¬xi ∨ ¬xj
これはリテラルの論理和、すなわち「節」であり、必ず充足されなければなりませんから hard 節です。
図2に対して hard 節を全て列挙すると、(¬x0 ∨ ¬x2), (¬x0 ∨ ¬x3) となります。
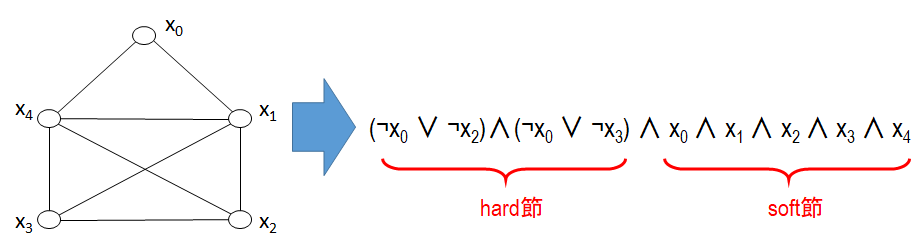
また、個々の変数は、1個のリテラルからなる節であり、最大クリーク問題における soft 節となります(より多くの変数を真にできれば、より大規模なクリークを見つけたことになる)。
このようにして作られた hard 節と soft 節の論理積を取れば、最大クリーク問題が Partial MaxSAT に置き換わります。
解法アルゴリズム
Partial MaxSAT の解法には、分枝限定法などに基づく厳密解法や、メタヒューリスティクスを用いた発見的解法などがあります。こうした解法の殆どは (われわれハードウェア設計者の視点からは) 純然たるソフトウェア・アルゴリズムであり、FPGA 上で実行することを前提に設計されているわけではありません。そのため、それらをそのままの形で FPGA へ移殖するだけでは高速化が難しいだけでなく、移殖そのものが困難なことも珍しくありません (例えば再帰呼出しや動的メモリ確保が多用されている場合など)。
また、FPGA は動作周波数が非常に低いデバイス (せいぜい数100MHz程度) であるため、高速化のためには並列処理が欠かせません。そのため、優れたアルゴリズムであっても並列処理できる部分が少ないものは FPGA 実装には向きません。一方で、いくら高速でも精度の低い解しか見つけることができないとあまり意味がありませんから、精度の高い解を見つけることのできるアルゴリズムを使うことが望まれます。理想的には精度が高くて並列性にも富んでいるアルゴリズムがいいのですが、そのような虫の好い話は簡単には転がっていないものです。
筆者らは、局所探索法という発見的解法に基づくソルバー[4]を使用しました。これは文献[1]の第2著者が開発したソルバーで、2014年に開催された MaxSAT 向けソルバーの国際コンテスト (MaxSAT Evaluation) において優秀な成績をおさめています[5]。 開発者によって Dist と命名されているため、これ以降 Distと表記します。
局所探索法は、適当な初期解から出発し、(1) 現在の解の近くにある別の解 (近傍解) の良し悪しを調べ、(2) その結果に基づいていずれかの近傍解で現在の解を置き換える、という操作を繰り返すことで、徐々に最適解へと近づいていく、という手法の総称です。
Dist を選んだ理由は幾つかあるのですが、研究の開始当初において最も優れたソルバーのひとつであったこと、これより以前に SAT の FPGA 解法を研究していたときの経験から、並列化しやすい解法であると判断したこと (一般的に、局所探索法では近傍解の数が数百から数万程度と多く、その良し悪しの評価、および、評価結果の比較等に並列性がある場合が多い) などが、主な理由です。
当初は Parital MaxSAT 全般を扱えるようにしたかったのですが、 Dist をそのまま FPGA に実装することが難しかったため、対象を最大クリーク問題に絞ることにしました。そうすると、省いてしまっても解の探索に影響しないサブルーチンが Dist の中に含まれています。それらを省くことにより、精度を維持したまま FPGA への実装をより容易とすることができます。このあたりに関しては次回に改めて述べたいと思います。
Dist
図3に Dist の全体像を示します。
まず初期解を作る必要がありますが、これは論理変数に対してランダムに真理値を割り当てることにより生成します。また、全ての hard 節に重み1を与えておきます。詳細は後述しますが、この重みは探索の状況によって増減します。ただし0以下にまで減らされることはありません。また、soft 節には重みは与えられません。
初期解の生成が終わったら、(a) 全ての論理変数の中からひとつを選択して、(b) その真理値を反転させます。

このようにして作られる新しい解 (言い換えると、現在の解に対してハミング距離が1だけ離れている解) が近傍解というわけです。ある解に対する近傍解の数は論理変数の総数に等しく、その中からより良いものを選ぶ必要がありますが、その方法は後述します (直観的には、真理値の反転を行った後、非充足な節ができるだけ少なくなるようなものを選ぶと良さそうに思えます)。(a) と (b) を、最大クリークが見つかるまで繰り返します。以上が Dist の概略です。
以降、 Dist における近傍解の選択の手法について少し詳しく説明します。まず、近傍解を選択するにあたって、その良し悪しを判断するための尺度について見ていきます。
近傍解の良し悪しの評価尺度
Dist では、hard score と soft score という数量を用いて近傍解の良し悪しを評価します。hard score と soft score は与えられた問題の論理変数ひとつひとつに対して定義される数量です。
当たり前ですが、論理変数の真理値を反転させると、 (i) 今まで非充足であったけれども充足される節もあれば、 (ii) それまで充足されていたのに非充足になってしまう節もあります。
論理変数 x の hard score は、x の真理値を反転させた場合に、(i) に該当する hard 節の重みの合計から、(ii) に該当する hard 節の重みの合計を引いた値を指します。また、x の soft score は、x の真理値を反転させた場合に、(i) に該当する soft 節の総数から、(ii) に該当する soft 節の総数を引いた値を指します。
hard score がより大きい変数を選び、その真理値を反転させれば、より多くの hard 節が充足へと転じるか、または、それまでなかなか充足されなかった hard 節が充足されることが期待できます。同様に、soft score がより大きい変数の真理値を反転させれば、より多くの soft 節が充足されることが期待できます。
近傍解選択の手法
Dist における近傍解の選択、すなわち、真理値を反転させる変数をどのように選択する方法を説明します。
まず、変数を2つの集合 H, S に振り分けます。H は hard score が正である変数の集合、S は hard score が0、 soft score が正である変数の集合です。真理値を反転する変数は、H が空でなければ H から選択し、H が空の場合は S から選択します。
H と S がともに空の場合、まず、hard 節の重みの更新を行います。具体的には、非充足な hard 節の重みを1だけ増やすか、または、充足されている hard 節の重みを1だけ減らします。前者が実行される確率は sp (0 < sp < 1) 、後者が実行される確率は 1 – sp となっています (つまり、サイコロを振り、出た目の値によって hard 節の重みを増減させる) 。
続いて、非充足な hard 節をランダムにひとつ選び、それに含まれている変数のうち、soft score が最大のものを選択します。非充足な hard 節がなければ、非充足な soft 節をランダムに選び、そこに含まれている変数をランダムにひとつ選択します。
3. まとめ
今回は、最大クリーク問題の Partial MaxSAT への変換と、Partial MaxSAT の発見的解法である Dist アルゴリズムについて述べました。
次回以降、 Dist アルゴリズムの FPGA への実装について触れていきます。
筑波大学 金澤 健治
参考文献
- [1] Kanazawa, K., & Cai, S., “FPGA acceleration to solve maximum clique problems encoded into partial MaxSAT,” IEEE 12th International Symposium on Embedded Multicore/Many-core Systems-on-Chip, pp. 217-224, 2018.
- [2] 平山,横尾, “*-SAT: SAT の拡張 (< 特集> 最近の SAT 技術の発展),” 人工知能学会誌, 25(1), pp. 105-113, 2010.
- [3] 越村,藤田, “SAT 技術の進化と応用~ パズルからプログラム検証まで~: 6. MaxSAT: SAT の最適化問題への拡張-MaxSAT ソルバーの活用法,” 情報処理, 57(8), pp. 730-733, 2016.
- [4] Cai, S., Luo, C., Thornton, J., & Su, K, “Tailoring Local Search for Partial MaxSAT,” 28th AAAI,pp. 2623-2629, 2014.
- [5] http://www.maxsat.udl.cat/14/