前回は、MaxSAT の一種である Partial MaxSAT の定義、最大クリーク問題の Partial MaxSAT への変換、局所探索法に基づく Parital MaxSAT の発見的解法である Dist アルゴリズム[1]について述べました。
今回は、Dist の FPGA 実装に当たっての難点と、それを回避するためにどのようにアルゴリズムの簡略化を行ったかについて説明します。
Dist アルゴリズム
図1に、Dist アルゴリズムの全体像を再掲します (ステップ5 〜 7 が、前回の記事の図3 のステップ5 にあたります) 。
基本的な手順を大まかに述べると、 全ての変数に対して hard score と soft score を算出し、その結果に基づいて変数をひとつ選択して、その真理値を反転させる、という操作を繰り返すことで、全ての hard 節と、できるだけ多くの soft 節が充足されるような真理値割当てを見つける、というものです。
ここで、全ての hard 節が充足されるような真理値割当てを実行可能解、実行可能解のうち、充足される soft 節が最も多いものを最適解といいます。
以後、真理値を反転させる操作のことをフリップと表記します。

hard score と soft score は、フリップされる変数を選択するための尺度で、次のような数量です。
- 変数 x の hard score : x の真理値を反転させた場合に、 非充足から充足に転じる hard 節の重みの合計から、その反対の (充足から非充足に転じる) hard 節の重みの合計を引いた値。
- 変数 x の soft score : x の真理値を反転させた場合に、 非充足から充足に転じる soft 節の総数から、充足から非充足に転じる soft 節の総数を引いた値。
ハードウェア化の検討
アルゴリズムの一連の手順のうち初期化の処理 (図1のステップ1〜3) は、探索の最初に一度だけ実行すればよく、処理全体に占める割合がそれほど高いわけではありません。そのため、ソフトウェアで実行し、その結果を FPGA にダウンロードするのが簡単です。
FPGA 実装の中心部分は解探索の処理、すなわち、図1のステップ4〜7 なのですが、 そのどこに並列性があり、また、どこに実装の難しさがあるのか見ていきたいと思います。
並列性の高い処理
最も並列化の効果が高いのはステップ6です。
変数 xf をフリップしたことにより score が変化する可能性があるのは、xf 自身と、xf をリテラルとして持っている節に含まれている変数です (以降、それらの変数の集合をlist(xf) で表します) 。
その数は多い場合で数1000に登り、そのできるだけ多くを同時にアップデートできれば高速化に非常に有効です (少ない場合では数個くらいしかない。問題によりばらつきがある) 。
実装上の難点
(a) hard 節の重みの読出しの並列化
hard score を求めるには、hard 節の重みを読み出す必要があります。重みを並列に読み出せるようにするには、FPGA のオンチップメモリ (Block RAMなど) を複数個使って重みを保持しておけば、Block RAM の数だけ一斉に読み出すことができます。しかし、読み出したい重みが特定の Block RAM に集中してしまうと、その Block RAM へのアクセスコンフリクトが発生します。
また、ひとつの重みに 20b 程度のデータ幅が必要となるため、hard 節の数が多いと、その全てを Block RAM に置くことができなくなります。そのような場合、FPGA ボード上の DRAM を使用することになりますが、そうすると一度に読み出せる重みの数が DRAM チップの数で抑えられてしまいます。バーストリードを使えば一度に読み出す重みの数を増やせそうですが、ランダムアクセスができないため、Block RAM と比べると並列に読み出せる重みの数を多くするのは難しくなります。
更に、 hard 節の重みが変わると、 その節に含まれている変数の hard score が変わるため、重みの更新が起こる度に hard score の再計算と、それに伴う集合 H, S のアップデートが必要となります。
(b) 変数のフリップに伴う集合 H, S, UH, US のアップデート
変数 xf のフリップに伴い、 list(xf) に含まれる変数の hard score が更新されると、それに伴って集合 H, S, UH の更新が必要となります。それぞれの集合において、多いと数1000ほどの要素が入れ替わります。
以上は並列処理をしないのであればどうということはないのですが、FPGA で性能を出す以上はそうもいかず、これらが Dist のハードウェア化にあたっての主な難点でした (改めて見直すと、実はそれほど難しくないと思われるものもありますが、当初は難しいと思っていました)。
アルゴリズムの簡略化
前回の記事でも述べましたが、 筆者らによる Dist の FPGA 実装[2]にあたっては、対象を最大クリーク問題に限定することにより、アルゴリズムの簡略化を行っています。それについて述べていきます。
簡略化その1
最大クリーク問題に限定すると、以下のような理由で、Dist における hard 節の重みの更新が起こらなくなります。また、集合 UH を持つ必要がなくなります。
重みの更新が起こらなくなる理由
Dist における hard 節の重みの操作は、
- 非充足な hard 節の重みのインクリメント
- 充足な hard 節の重みのデクリメント 、ただし、重み 1 の場合はデクリメントしない
のどちらかが確率的に実行される、というものでした。
しかし、非充足な hard 節がある場合、集合 H が空でないため、図1の 4-c が実行される条件が成立しません。そのため重みのインクリメントが行われることはありません。また、hard 節の重みの初期値は1ですから、そのインクリメントが行われないということは、重みが2以上になることはないく、従って充足な hard 節のデクリメントも行われません。
結局、hard 節の重みは 1 のまま変わることがなく、重みを明示的に保持する必要がなくなります。
以下に、非充足な hard 節があると集合 H が空でない理由を述べます。
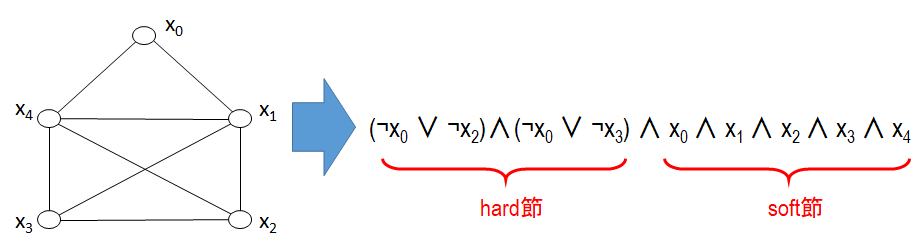
まず、前回掲載した、最大クリーク問題から作られた Partial MaxSAT の例題を図2に再掲します。
hard 節と soft 節のリテラルにそれぞれ着目すると (リテラルの定義はこの連載の第1回を参照してください) 、hard 節に含まれるリテラルの個数は2であること、hard 節に含まれるリテラルには全て論理否定があること、soft 節のリテラルには論理否定がないことに気がつきます。
これは、最大クリーク問題を Partial MaxSAT に変換する際の hard 節と soft 節の作り方 (第2回を参照) に由来しています。
リテラルにおける論理否定の有無をリテラルの極性といいます。上述のように、最大クリーク問題の場合、任意の hard 節のリテラル同士 (または任意の soft 節のリテラル同士) は全て同じ極性を持っています。
次に、非充足な hard 節をひとつ考え、 ¬x ∨ ¬y と置きます。
¬x ∨ ¬y は非充足なので、x = 1 です。
ここで、x の hard score を考えます。 否定のつかないリテラルを含む hard 節はありませんから、 x をフリップすることにより充足から非充足へ転じる hard 節は存在しません。 一方、¬x ∨ ¬y は非充足から充足へ転じます。つまり、 x のフリップにより非充足から充足に転じる hard 節が少なくとも1つ存在します。そのため、hard score の定義より、x の hard score は正です。集合 H は hard score が正の変数の集合ですから、x ∈ H です。
以上から、非充足な hard 節があるとき、H は空でないことがわかります。
集合 UH が不要となる理由
非充足な hard 節が存在する場合、集合 H が空でないため、フリップされる変数は必ず集合 H の中から選択されます。そのため、図 1 の 4-c-ii が実行されることがありません。
すなわち、フリップされる変数の選択のために、UH を明示的に持つ必要がなくなります。
UH がないと、現在の解が実行可能解であるかどうかの判断がつかないように思えますが、これは、集合 H が空であるかどうかを調べれば判断することができます。これは、 hard score の定義と、最大クリーク問題における hard 節の性質 (全ての hard 節のリテラルが同じ極性を持つこと) から、H が空であれば 全ての hard 節が充足しているためです。
(繰り返しになりますが、以上は最大クリーク問題に対象を限定した場合にのみ当てはまります。)
簡略化その2
soft 節の構成要素がリテラル1個であることから、図1の 4-b と 4-c-iii が、以下のように簡略化されます。
まず 4-b ですが、どの soft 節もリテラルを1つしか持たないため、soft score は1か -1 のどちらかとなります。従って、4-b (soft score が最大のものを選択、ただし候補が複数ある場合は乱択) は、soft score が1の変数の中から乱択、という処理に置き換えることができ、soft score の大小比較が省略されます。
次に 4-c-iii ですが、soft 節は論理変数そのものなので、真理値が0の論理変数を乱択すれば、4-c-iii と等価な処理をしていることになります。
最大クリーク問題専用 Dist アルゴリズム
図3に、対象を最大クリーク問題に絞って簡略化された Dist アルゴリズムを示します。

hard 節の重みを持つ必要がなくなったため、「ハードウェア化の検討」の節で実装上の難点として上げた項目 (a), (b) のうち、(a) は考慮する必要がなくなりました。(b) については、集合 UH がなくなったことにより、やや緩和されてはいますが、完全に解決したわけではありません。これについては次回に述べたいと思います。
まとめ
今回は、Dist アルゴリズムの FPGA 実装に当たっての難点を述べ、処理可能なアプリケーションを最大クリーク問題に限定するとその難点の解消につながることを示しました。
次回から、最大クリーク問題向けに簡略化された Dist アルゴリズム (図3) の FPGA 実装について触れていきたいと思います (ここまでなかなか回路の話が出てきませんが、次回以降は出てくる予定です) 。
筑波大学 金澤 健治
参考文献
[1] Cai, S., Luo, C., Thornton, J., & Su, K, “Tailoring Local Search for Partial MaxSAT,” 28th AAAI,pp. 2623-2629, 2014.
[2] Kanazawa, K., & Cai, S., “FPGA acceleration to solve maximum clique problems encoded into partial MaxSAT,” IEEE 12th International Symposium on Embedded Multicore/Many-core Systems-on-Chip, pp. 217-224, 2018.