前回までの説明で FPGA (小人さん) を動かすための仕組みについて大雑把な話をしてきました。小人さんは流れ作業で仕事をするので、データフローのような記述をするとちゃんと変換できます。しかし、プログラム言語からハードウェア記述言語に変換する高位合成ツールは、少し難しいことをしていました。さらに、配置配線ツールは時間が掛かります。さて、最終回である今回は、これまであいまいにしてきた小人さんの正体に迫っていきたいと思います。
CPU はなぜプログラムを実行できる?
第一回でも説明しましたが、CPU は「プログラムを書いて、コンパイラなるなぞ変換で CPU が理解できる形に作り直します。それをメモリ上に置いて、実行」します。では、何が実行するのでしょうか?
ここで簡単に CPU の動作の仕組みについて説明します。
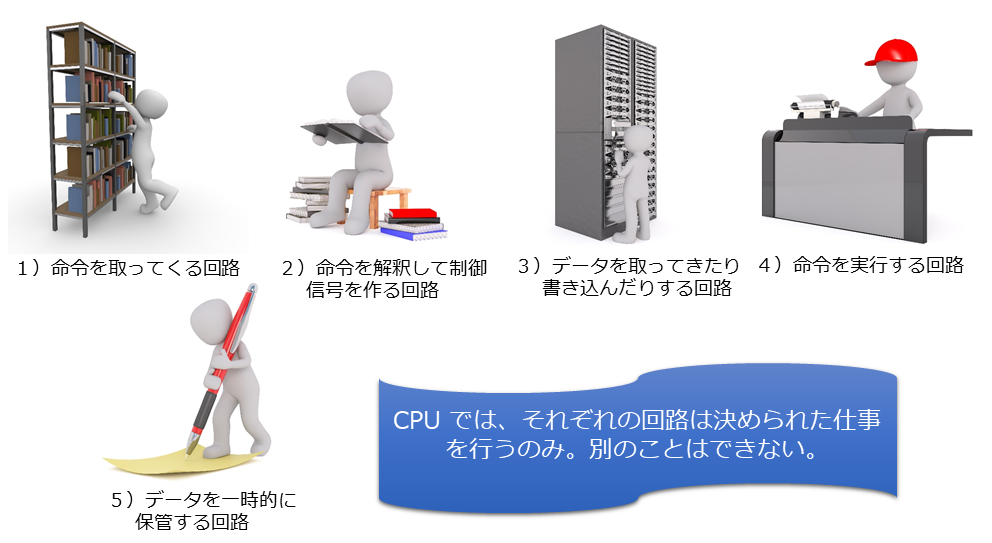
CPU で実行するプログラムは、コンパイラによって理解できる形式に変換されますが、「理解できる」形式とは、CPU に対する「命令」のことです。つまり、第三回でも説明した通り、プログラムに書かれた手続き的な処理は、コンパイラによって命令列に変換されます。そこで、CPU はこの命令をメモリ上から読み出して実行するわけですが、それにはざっくり次の5つの回路が必要です。1)命令を取ってくる回路、2)命令を解釈して制御信号を作る回路、3)データを取ってきたり書き込んだりする回路、4)命令を実行する回路、5)データを一時的に保管する回路です。ここで重要なのは、4)の命令を実行する回路です。それ以外の回路は、命令を実行するまでに必要な前処理と実行後の後処理をする副次的な回路です。もちろん、CPU はこれらが揃っていないと機能しませんが、4)以外が別の手段であっても構いません。これを踏まえて、実際の動作を見ていきます。
CPU の動作と命令
例として、うるう年の判定を行うプログラムで説明します。うるう年の判定は、1)4で割り切れる年、2)しかし、100で割り切れる年は除く、3)しかし、400で割り切れる年は含む、となります。C言語のプログラムの抜粋を下に示します。
if (year % 400 == 0 || (year % 4 == 0 && year % 100 != 0)) {
printf("うるう年です");
} else {
printf("うるう年ではありません");
}うるう年を判定する部分は、if 文の括弧の中の判定式です。このコードがコンパイラで命令列になったときに、どんな命令が出てくるでしょうか?
最初は年を400で割った余りを求めています。これは剰余演算命令です。次に剰余が0かどうかを判定しています。これは比較命令です。そして、次の条件に行くところで論理和を行っているので、論理和命令も出てきました。以下、剰余演算命令、比較命令、論理積命令、剰余命令、比較命令となります。また、if 文は条件分岐命令で実現します。
つまり、ここで出てくる命令は、剰余命令、比較命令、論理和命令、論理積命令、条件分岐命令の全部で5種類です。とある CPU が剰余命令を持っていなければ、コンパイラはその部分を除算命令に置き換えます。さらに、除算命令で剰余を求められない場合は、乗算命令と減算命令を用いて剰余を求めるコードにします。このように、CPU もアーキテクチャが異なれば、持っている命令も異なります。それでも同じように動作するのは、その CPU に合った命令列をコンパイラが出力するからです。
また、この5種類の命令は、すべて「4)の命令を実行する回路」中で処理されます。この4)の回路を ALU (Arithmetic and Logic Unit) /算術論理演算装置と言います。これは算術演算(四則演算)と論理演算を実行するディジタル回路から出来ています。
CPU での実行のしくみ
実行の仕組みを整理すると、CPU でプログラムを実行するということは、プログラムを 1)CPU が持っている命令に分解し(コンパイラ)、2)命令列をつくり(リンカ、コードジェネレータ)、それをメモリ上に配置し、3)命令を読み出して解釈しながら、4)データをもってきて演算を行うこと、に他なりません。
つまり、CPU は自分の持っている資源を使い倒すことでプログラムを実行しているのです。それなので、やりたいことを実現する命令を持たなければ、他の命令の組合せで同じことを実現します。CPU は、持っている命令の種類が多ければ回路が複雑になり、少なければプログラムが複雑になるという関係になります。ちょうどよい命令を持つことが如何に大切かわかると思います。これを命令セットアーキテクチャと言い、マイクロアーキテクチャと共に CPU の根幹をなす重要な部分です。
FPGA の場合は、何が実行しているのか?
さて、前置きが長くなりましたが、次は FPGA ではどのように実行するのかを見ていきます。
CPU が命令を実行する ALU のような回路を使い倒すと説明しましたが、FPGA では命令に相当する回路を並べてデータを流します。第三回で仕事を配置し接続(配線)するといっていた「仕事」が命令に相当する部分です。そして、データフローを作るために配線をしました。
CPU と同じやり方を FPGA で実行してみる
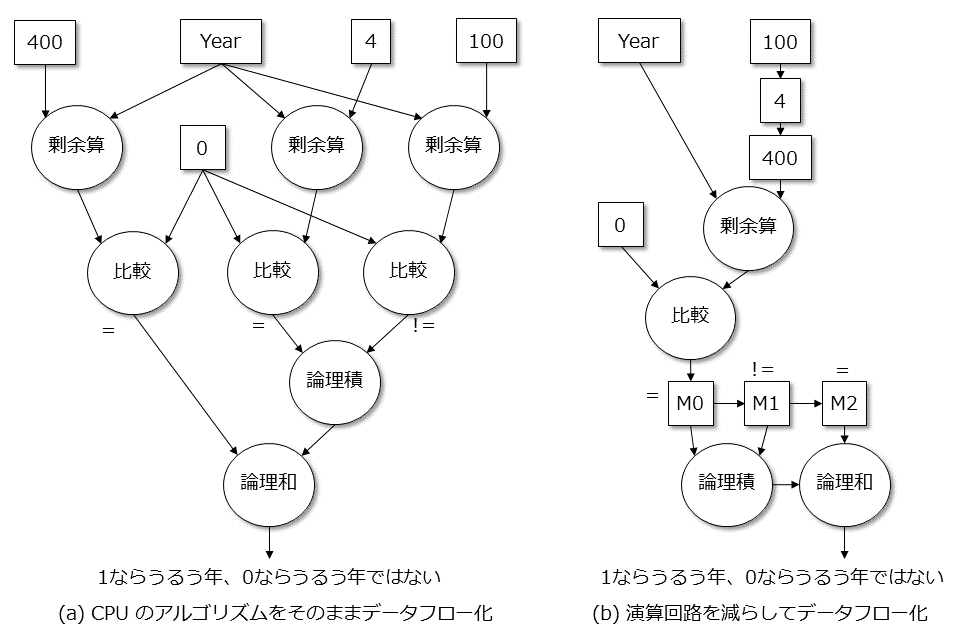
このうるう年の判定処理を行う回路を考えたとき、CPU と同じ方法でやってみると次のようになります。このとき、1)命令を取ってくる回路、2)命令を解釈して制御信号を作る回路、3)データを取ってきたり書き込んだりする回路、5)データを一時的に保管する回路は、CPUとは異なり、データフロー的な回路になります。つまり、先程示した通り、4)の命令を実行する回路以外が別の手段であるケースになります。
左図のように、そのままデータフローを回路にすると剰余回路と比較回路が3つも出てきてしまいます。CPU では命令として3回出てきても、実行する回路は1つです。右図のように剰余回路と比較回路を1つずつにして、データを切り替えるようにすると、データフロー的な動作ではなくなってしまいます。
この2つは、FPGA においては空間と時間の相互変換が可能であることを示しています。つまり、時間をかければ回路を小さくできる(空間を少なくできる)し、空間を大きくすると時間が小さくなる、というわけです。CPU では命令の種類と回路規模のバランスが大切だったように、FPGA では時間と空間のバランスを考えなければならないのです。
FPGA ならではのやり方は?
どうも CPU のプログラムのままでは、帯に短し襷に長しという状態です。では、FPGA ならではの解はないのでしょうか?
もちろん、あります。
CPU では命令は固定なので、それを処理する ALU も固定的です。固定的とは、CPU が作られた時から変わることはないという意味です。それに対して、FPGA は小人さんに与える仕事を変えれば違うことができます。つまり、ここでは剰余回路、比較回路という2種類を用いていましたが、これらを変更することができるということです。そこで、処理のやり方を変えます。
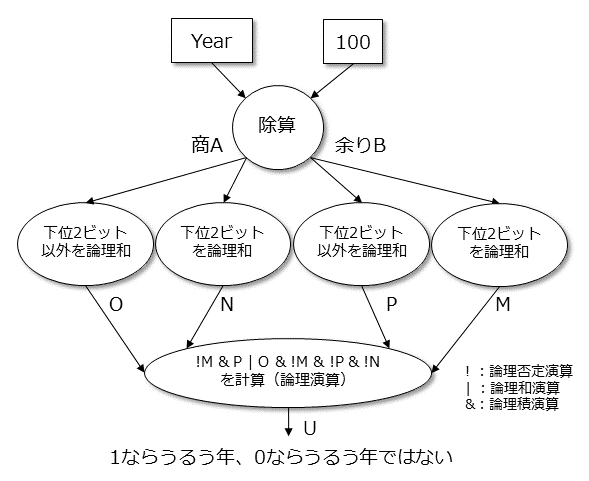
うるう年は、1)4で割り切れる年、2)しかし、100で割り切れる年は除く、3)しかし、400で割り切れる年は含む、という条件ですが、剰余回路を使わなければならないわけではありません。そこで次のやり方で判定します。Year が判定したい年の入力で、基本的に2進数で入力されるものとします。以下の計算は10進数で表記していますが、すべて2進数での計算です。
- Year ÷ 100 を実行し、商 A と余り B を求める
- 商A の下位2ビットを論理和演算し N とする。
- 商A の下位2ビット以外をすべて論理和演算し O とする。
- 余りB の下位2ビットを論理和演算し M とする。
- 余りB の下位2ビット以外をすべて論理和演算し P とする。
- U = !M & P | O & !M & !P & !N を計算する。
(! は論理否定演算、| は論理和演算、& は論理積演算を表します)
この結果、U が1ならうるう年、0ならうるう年ではないとなります。なぜだかわかりますか?
余りB は100で割った余りですから、これの下位2ビットが論理和して0ということは、4の倍数であることを示しています。10進数の4は2進数の (100)2 ですので、4で割った余りは(01)2, (10)2, (11)2のどれかです。つまり、元の数字の下位2ビットを見れば4で割り切れるかどうかがわかります。P は余りの上位ビットが0かではないかを示します。
商A の下位2ビットを見ているのも同じで、ここが00なら4で割り切れたということですから、100で割って、4で割った結果なので、結局、400で割って割り切れるということです。同じく O は商の上位ビットが0かではないかを示します。
ということで、最初の”!M & P”は「100で割り切れないけど、4で割り切れる年」という条件、後の”O & !M & !P & !N”は「400で割り切れる年」という条件を示しています。
この FPGA での処理方式のポイントは、CPU で剰余演算、比較演算のような決められた演算を行う回路で実行するのではなく、必要に応じて必要な回路で処理するということです。つまり、FPGA は回路を変更する能力があるということです。まぁ、これは最初から言っていることですが…。また、このように回路で処理する方法をハードウェアアルゴリズムと言います。一般的にアルゴリズムというとプロセッサで処理するイメージですが、FPGA や LSI で実現する場合は、このハードウェアアルゴリズムが重要になります。それはハードウェア資源も考慮したアルゴリズムになっているからです。
この場合でも、除算回路が1つで後は論理演算で処理ができますので、最初の CPU のアルゴリズムと比較すると格段に小さい回路になります。一方、このハードウェアアルゴリズムを CPU でやろうとすると、下位の2ビットを取り出す操作や論理演算命令をたくさん (13回も!) 実行しなければならないのでかなり損です。つまり、それぞれに合った方法というのがあるものなのです。
小人さんの正体
さて、CPU は自分の持っている回路資源を使い倒すことでプログラムを実行していますが、FPGA では必要に応じて回路資源を書き換えることで実行します。この回路資源とは、ディジタル回路そのものですから、任意のディジタル回路が実現する方法がなければなりません。
一般的に、LSI のディジタル回路は、剰余演算回路のようにまとまった機能を分解すると、論理ゲートと呼ばれる論理積や論理和などを行う回路に分解できます。さらに分解すると、トランジスタの回路になり、それをさらに分解するとシリコン原子になっていきます。
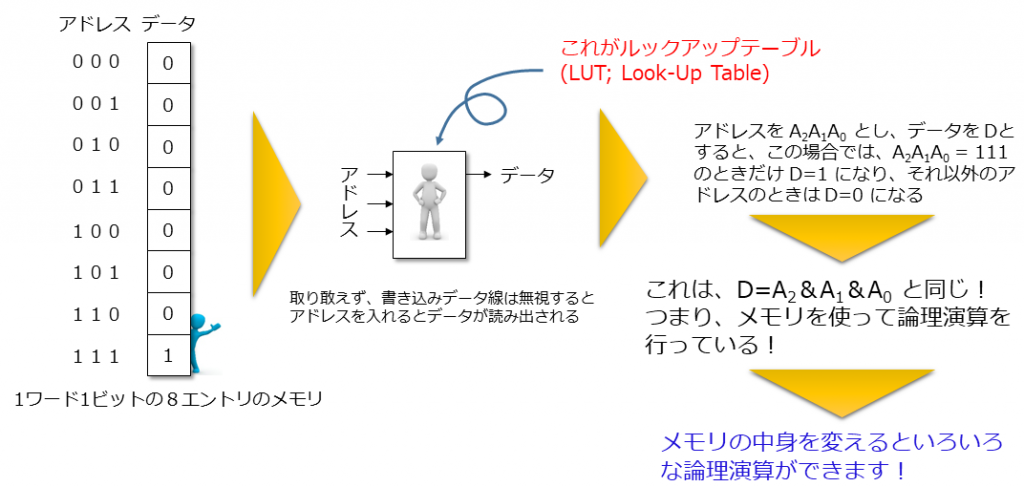
FPGA は、この2番目の論理ゲートの代わりにルックアップテーブル (LUT; Look-Up Table) と呼ばれるメモリを用います。このメモリに値を書き込んでおくと書き込んだ値に対応した論理ゲートと同じ働きをします。これが小人さんの正体です。
下図の例では、LUT に入力されたアドレスにしたがって、メモリの値を読み出しているだけにもかかわらず、まるでアドレスの3ビット A0, A1, A2 を論理積演算しているように見えます。また、このメモリに書き込んでおくデータを変えればいろいろな論理関数を実現できます。例えば、(011111111)2 を書いておけば論理和演算になるというわけです。
この LUT は、一つの FPGA の中に数百万個も入っているので、頻繁に書き換えることはできません。通常は、電源が入ったときにいっぺんに書き込み、それ以降は書き換えないで動くのです。最近の FPGA では、部分的に書き換えることができるものもありますが、プログラムのようにちょこちょこ読み書きしながら動くものではないのです。なので、小人さんは一度覚えるとその仕事をやり続けるようになるのです。
まとめ
最終回のまとめです。
これまで「小人さんの世界」を通じて FPGA と CPU の本質的な違いや難しさを紐解いてきました。うまく説明できていると良いのですが、難しかったでしょうか?なんとなくイメージができただけでも役に立つと信じたいところです。
さて、この最終回は小人さんの正体がメモリであるというところで終わってしまいますが、このコースでは、FPGA ってどうやって生まれてきたかとか、GPU との関係とか、なんでメモリで論理回路ができるのとか、まだ FPGA の不思議に応えきれなかったところや説明が足りないところが多くあります。また機会があれば、この辺りもお話したいと思います。個人的には、この5回のシリーズを楽しんでいただけたならそれで十分ですが、 FPGA についての本質的な理解が少しでも進んでくれたら望外の喜びです。そして、みなさんが「小人さんの世界」にどっぷり漬かっていくことを願っています。
宿題
A, B, C の3つの数の入力があります。これらの数値は三角形の辺の長さを示しています。任意の入力があったとき、それらで三角形を作ることができるかどうかを判定する処理を、プログラムと回路による最適な方法について考えなさい。また、その違いについても説明しなさい。
熊本大学 大学院先端科学研究部 飯田全広
※ 主に Peggy und Marco Lachmann-Anke による Pixabay からの画像を使用しました。