FPGA 向けの真性乱数生成器 (TRNG) の設計法に関するコースの第4回です.今回は、SR ラッチを禁止状態から保持状態へと移行させた時の挙動 (メタスタビリティ) を用いた TRNG の構成と、その改良について紹介します。
なお、この記事の最後に紹介するラッチ-ラッチ構造 (Latch-latch composition) に関する論文 [1] は、電子情報通信学会の Electronics Express (ELEX) 論文誌に掲載されています。オープンアクセスの電子ジャーナルなので、(英語で書かれていますが) 誰でも無料で読むことができます。
また、この研究は私が TRNG の研究をするきっかけになったものでもあります。当時所属していた研究室の主宰であり、論文の共著者でもある豊橋技術科学大学の市川周一教授からは、この研究に関しても多くのヒントを頂きました。この場を借りて改めて御礼申し上げます。
SR ラッチの動作
SR ラッチの基本的な動作
ディジタル回路において最も基本的な記憶素子の1つが、下図に示す SR ラッチ です。RS ラッチとも言いますが、ほぼ同義です。また、慣例的に SR (RS) フリップフロップともよばれます (厳密にはフリップフロップではありませんが)。教科書によっては、入力のバブル (= NOT ゲート) を省き、入力を S、R で表現することもあります。
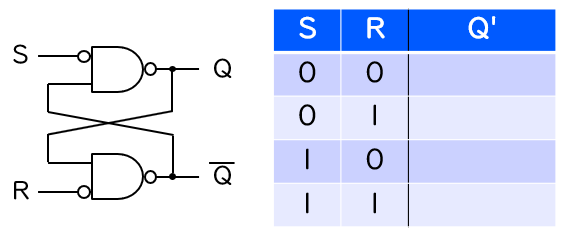
第1回ではいきなり完全な特性表を載せてしまいましたが、ここではもう少し詳しく SR ラッチの基本的な動作を確認します。上下の NAND ゲートの出力をそれぞれ Q、Q としたとき、入力の各パターンに対して出力がどう変化するかを考え、特性表を順番に埋めてみましょう (SR ラッチの基本的な動作を十分把握している場合は、この節は読み飛ばして構いません)。
まずは S = R = ‘0’ の場合を考えてみます。このとき、NAND ゲートの外側の入力にはその反転の ‘1’ が入力されます。NAND ゲートは両方の入力が ‘1’ のときには ‘0’、それ以外では ‘1’ を出力しますから、この NAND ゲートは内側の入力に対する NOT ゲートとして動作することになります。
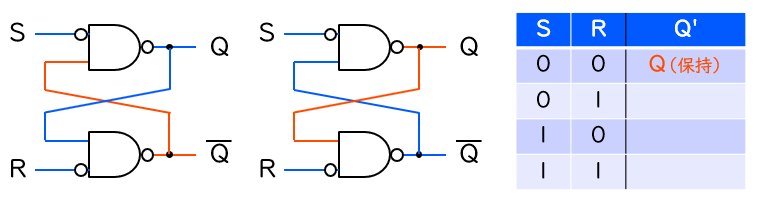
この場合、下図に示す2通りのパターンが考えられます。青線が値 ‘0’ の信号、赤線が値 ‘1’ の信号を表します。現在の Q を ‘0’ と仮定した場合 (図の左側) でも ‘1’ と仮定した場合 (図の右側) でも、すべての NAND ゲートの出力を矛盾なく定めることができます。これが意味することは、SR ラッチは2つの安定な状態を持ち、S = R = ‘0’ のとき現在の状態をそのまま保持しつづける、ということです。
次に、S = ‘0’ で R = ‘1’ の場合を考えてみると、下図の左側に示す結果が得られます。下側の NAND ゲートの外側の入力には R を反転した ‘0’ が入力されます。NAND ゲートは入力のうち1つでも ‘0’ があれば ‘1’ を出力しますから、下側の NAND ゲートの出力は ‘1’ で確定します。この結果、上側の NAND ゲートの出力、すなわち出力 Q は (NAND ゲートの入力が両方 ‘1’ なので) ‘0’ に切り替わります。
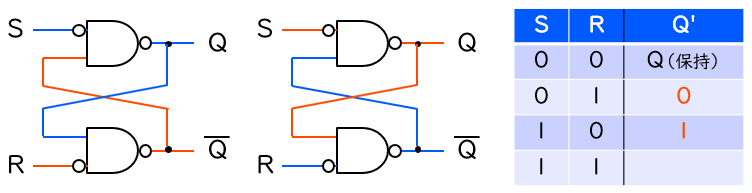
S = ‘1’ で R = ‘0’ の場合は、先ほどと上下を逆さまにすると同じ議論が成り立ち、その結果は上図の右側に示すものとなります。結局のところ、S と R のどちらかが ‘1’ の場合は、S (セット) が ‘1’ ならば Q は ‘1’ に切り替わり、R (リセット) が ‘1’ ならば Q は ‘0’ に切り替わることになります。
ここまでで、‘0’ と ‘1’ の2つの状態を持ち、外部から状態を相互に切り替えられるという、記憶回路として最低限の機能が SR ラッチには備わっていることが確認できました。さて、入力パターンとして最後に残った S = R = ‘1’ の場合はどうなるでしょうか。下図にその結果を示します。
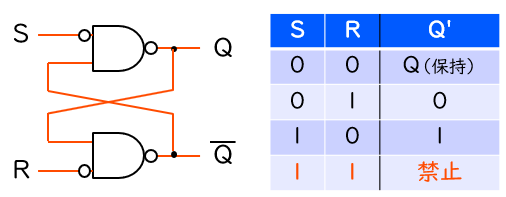
両方の NAND ゲートの外側の入力が S、R の反転である ‘0’ となるため、出力は ‘1’ で確定します。つまり、Q も Q も ‘1’ という、よくわからない状態に陥ってしまいます。そのため、このよくわからない状態はそもそも使わないこと (禁止) にする、もし使った場合の出力は不定とみなす……というのが、SR ラッチで S = R = ‘1’ としたときの教科書的な説明です。
SR ラッチのメタスタビリティ
この記事では議論を更に進めて、SR ラッチを S = R = ‘1’ の禁止状態から S = R = ‘0’ の保持状態へと移行させる場合を考えます。もしも S や R を ‘0’ に切り替えるタイミングが互いにズレていれば、その途中にセット・リセットのいずれかの動作を経由することになります。そのため、S を ‘0’ にするのが早ければ (リセットを経由して) Q は ‘0’ に、R を ‘0’ にするのが早ければ (セットを経由して) Q は ‘1’ と定まります。
S と R を ‘1’ から ‘0’ に全く同時に切り替えた場合にはどうでしょうか。第2回でリングオシレータの動作を解析したときと同様に、各 NAND ゲートが τ の伝搬遅延をもつとして考えてみます (ただし、NAND ゲート前段のバブルの伝搬遅延は無視します)。時刻0で S と R を ‘0’ に切り替えたときのタイミングチャートを、下図に示します。
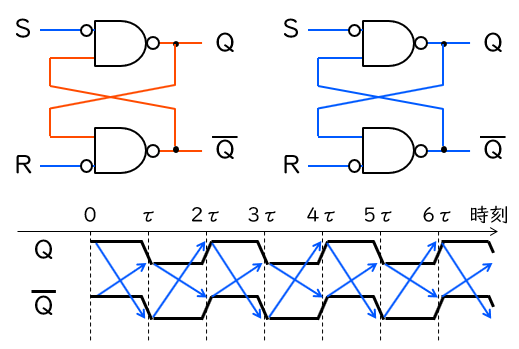
時刻 τ では、NAND ゲートの全ての入力が ‘1’ となったことから、両方の NAND ゲートの出力が ‘0’ に変化します。これにより、時刻 2τ では NAND ゲートの内側の入力が ‘0’ であるため、両方の NAND ゲートの出力が ‘1’ に変化します。以降はこれを繰り返します。結果として、SR ラッチは周期 2τ で発振することになります。
ただ、リングオシレータのときとは異なり、この発振はほとんどの場合長くは続きません。というのも、回路内部での熱雑音や、回路を構成するトランジスタの特性のばらつきなどの影響で、どこかのタイミングで ‘0’ と ‘1’ の比率 (デューティ比) に差が現れます。そして、ひとたびデューティ比に差が生まれると、信号が8の字を1周するたびにその差は増幅されることがわかっています [2]。最終的には、いつかはデューティ比は 0 % か 100 % のいずれかになる、すなわち Q は ‘0’ か ‘1’ のいずれかに収束することとなります。しかし、それがどちらになるかはわかりません。
この S と R を ‘1’ から ‘0’ に全く同時に切り替えた場合の状態のことを、メタステーブル (準安定)とよびます。理論上は永久に発振を繰り返すものの、現実には次第に安定な状態のどちらかに落ち着くというのが、「準」安定とよぶ意味合いです。
これをたとえるのに、坂道をボールが転がるたとえがよく使われます。ボールはなるべく低い方へと転がろうとしますが、坂道がどういう形をなすかは、入力のパターンによって決まります。保持・セット・リセットのそれぞれの状態における坂道の形を下図に示します。
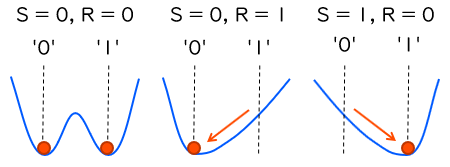
S = R = ‘0’ は、ちょうど ‘0’ にあたる場所と ‘1’ にあたる場所の両方に谷を持つ形 (2つの安定な状態をもつ) となります。S = ‘0’ で R = ‘1’ ならば ‘0’ にあたる場所のみに谷ができ、S = ‘1’ で R = ‘0’ ならばその逆です。これらの場合はボールは対応する谷へと転がっていくことになります。
S = R = ‘1’ の場合を下図の左側に示します。このとき、ちょうど ‘0’ と ‘1’ の中間に谷が生じ、ボールはそこへと転がります。ここから S と R を同時に ‘0’ へと切り替えると、坂道の形は上図で示した S = R = ‘0’ の形に一気に移行します。
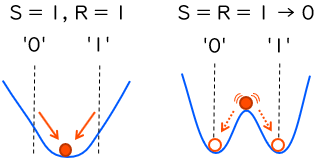
すると、上図の右側に示すように、なんとボールはちょうど ‘0’ と ‘1’ の間にある山の頂上に乗ってしまいました。これはこれでボールに何の力も加わらなければ、山の頂上にとどまり続けることができるでしょう。しかし実際には、何かの弾みでボールは ‘0’ か ‘1’ のどちらかの方向に転がりはじめ、谷底へと落ちてしまいます。こうした山の頂上に乗った状態がメタステーブル状態であり、この一連の現象をメタスタビリティといいます。
SR ラッチを用いた TRNG の構成法
LUT ラッチ
メタステーブルからどちらの安定な状態に移行するかは予測ができませんので、これを利用して TRNG を構成できます。SR ラッチが完全にバランス良く作られていて、上のたとえで言えばボールがぴったり山の頂上に乗るようになっていれば、1個の SR ラッチで TRNG が構成できるはずです。
しかし、現実にはトランジスタや配線には特性のばらつきが生じます。ややバランスが悪ければ ‘0’ や ‘1’ のどちらかの出現確率が高くなります。更にバランスが悪ければ ‘0’ か ‘1’ のどちらか片方しか出力しなくなります (実際のところこれが大半なのですが)。これを解決するために、SR ラッチを多数並べて、その出力を XOR することで、’0′ と ‘1’ の出現率の偏りを解消しています。
この方法による TRNG の FPGA 実装の1つが、Hata と Ichikawa により Xilinx 社の旧世代 FPGA (Virtex-4) 向けに提案された LUT ラッチ方式 [3] です。その構成を下図に示します。青色で示すのが FPGA 内部の LUT (Look-Up Table)、緑色が D フリップフロップ (D-FF) です。また、灰色の枠は Xilinx 社の FPGA における論理ブロック (スライス) の境界です。なお、S と R は共通化 (および反転) して1つの入力 ASRT としています。
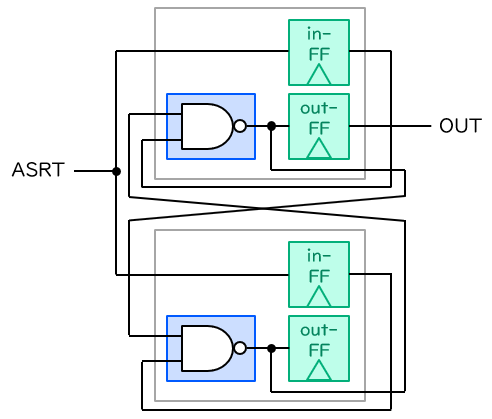
メタステーブル状態へうまく移行させるためのポイントは、S と R を ‘1’ から ‘0’ に全く同時に切り替えることです。そのために、NAND ゲートに対応する LUT を2つの Slice に分けて配置し、入力をそれぞれのスライス内の D-FF (図中の in-FF) にいったん保存するようにしています。また、ハードマクロという、素子間の配線まで手動で指定する形式でラッチを実装することで、D-FF から LUT までの配線を可能な限り揃えています。
こうした調整によりメタステーブル状態がより発生しやすくなれば、必要なラッチの個数が少なくても、偏りのない乱数が得られます。実際、彼らの評価結果によれば、乱数の生成速度にもよりますが、64~128個程度のラッチで NIST の試験に合格する乱数が生成できたとのことです。
しかしながら、従来式のハードマクロの生成法は、現在の Xilinx 社の開発環境である Vivado ではもはやサポートされていません。複雑な制約ファイルを記述すれば同様の機能が実現できるかもしれませんが、それはそれで可搬性 (ポータビリティ) に難があります。可搬性を鑑みれば、Verilog HDL などの RTL 記述レベルで記載できる、ソフトマクロという形式で実現することが望ましいです。
そのため、まずは Artix-7 向けにソフトマクロで LUT ラッチ方式の TRNG を実装してみました。しかしその結果、必要なラッチの数は640個程度と極めて多くなってしまうことがわかりました。これはハードマクロとソフトマクロの差もありますが、前回と同様に、新しい FPGA はより誤動作しにくいように作られているという理由もあるようです。
Xilinx FPGA のレジスタの特殊な使い方
ということで、SR ラッチを用いた TRNG を最近の Xilinx 社の FPGA で効率的に実現するにはもうひと工夫必要です。その工夫について説明する前に、同社の最近の (Spartan-6 以降の) FPGA におけるスライスの構造を説明しておきます。スライスの構造のうち、細々した回路を省いたものを、下図に示します。
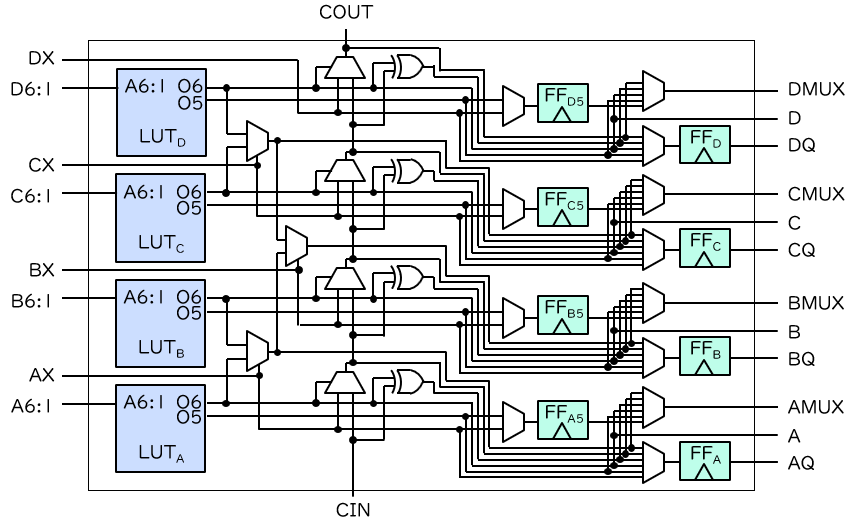
最近の Xilinx 社の FPGA では、1個のスライスには6入力の LUT が4個、D-FF が8個用意されています。また、LUT の脇にある3個のマルチプレクサは、LUT を複数使って7入力や8入力の論理関数を実現するために用いられます。さらにその横にあるマルチプレクサと XOR ゲートの組は、加算時の桁上げを高速に計算するための専用のロジック (キャリーチェーン) です。FPGA で組合せ回路を実現するのに最も使われるのは LUT ですが、LUT 以外で一部の組合せ回路を実現する方法がある、というのがここでのポイントです。
ここでは、スライス内の D-FF は、ゲートつき D ラッチとしても構成可能であることに注目します。D-FF とは異なり、ゲート入力 (D-FF のクロック入力に相当) が ‘1’ のときはいつでも、D の値が Q に反映されます。このゲートつき D ラッチは、非同期クリア入力 C またはプリセット入力 P をもちます。これらが ‘1’ の場合には、他の入力にかかわらず、出力はそれぞれ ‘0’、’1′ に固定されます。
この非同期クリア入力 C をもったゲートつき D ラッチに対し、ゲート入力を ‘1’ に固定したときの様子を下図に示します。C = ‘1’ の場合には Q = ‘0’、そうでなければ Q = D ですから、対応する論理関数は Q = D・C です。つまり、この回路は AND ゲート (ただし一方の入力は反転) として動作します。
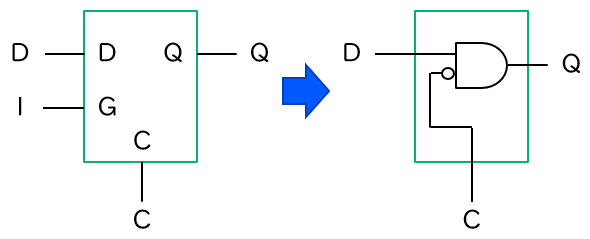
同様に、非同期プリセット入力 P をもったゲートつき D ラッチからは、Q = D + P、つまり OR ゲートが構成できます。別にこれらは隠し機能というわけではなく、しっかり Xilinx 社のユーザガイド (UG474) にも明記された正当な使用方法です。
そして、スライスの内部構造上、全ての非同期クリア入力には同一の入力が与えられます。SR ラッチの S と R を全く同時に ‘1’ から ‘0’ に切り替えるという目標は、これを使って実現できそうです。
ラッチ-ラッチ構造
以上を踏まえて、我々は SR ラッチを用いた TRNG の新たな実装法である、ラッチ-ラッチ構造を編み出しました。これは、スライス内の D-FF のラッチ機能を使った SR ラッチであることから命名しています。その構成を下図に示します。
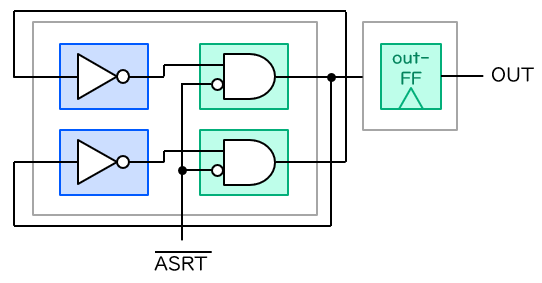
ゲートつき D ラッチの非同期クリア入力には、S = R にあたる入力を与えます。また、これだけだと NAND ではなく AND になってしまうので、LUT で NOT ゲートを作成し、AND ゲートの出力を反転させます。なお、D-FF を使うかゲートつきラッチを使うかはスライスごとに設定するため、出力保持のための D-FF (図の out-FF) は別のスライスに置きます。
このラッチ-ラッチ構造を評価した結果、320個のラッチで NIST の試験に合格する乱数が生成できました。LUT ラッチでは640個でしたので、必要な回路素子の数はおおむね半減したことになります。このときの乱数の生成速度は 20 Mbit/s でした。またその後の研究で、複数回の乱数生成結果を累算することで、生成速度が 1.33 Mbit/s まで低下するかわりに、必要なラッチの個数は16個まで削減できることもわかっています [4]。
これはかなりマニアックな FPGA の論理素子の使い方かもしれません (実は次回もそうなのですが)。ただ、より一般的な回路でも、細かいタイミングが重要な設計では、FPGA がどういう仕組みで動いていて、どんな内部構造をもつのかを理解しておくことは、最適な設計へのヒントとなることでしょう。
まとめ
今回は、SR ラッチのメタスタビリティを用いた TRNG について詳しく紹介しました。今回の要点は以下のとおりです。
- SR ラッチを禁止状態から保持状態へと一気に遷移させるとメタステーブル状態になり、これを経た SR ラッチの最終的な出力は TRNG に応用できる。
- SR ラッチをメタステーブル状態へうまく移行させるには、S と R を ‘1’ から ‘0’ に全く同時に切り替えることが重要である。
- 細かいタイミングが重要になる設計に臨む際には、FPGA の論理ブロックの内部構造を理解しておくとよい。
次回で紹介する TERO 型 TRNG は、SR ラッチのメタスタビリティを扱う点は似ているものの、その出力が安定するまでの時間 (発振の回数) に着目する点が、今回紹介した TRNG と異なります。次回はその詳細と改良について扱ったあと、コース全体の総括をしたいと思います。
愛知⼯業⼤学 藤枝直輝
参考文献
- [1] N. Fujieda and S. Ichikawa: A Latch-latch Composition of Metastability-based True Random Number Generator for Xilinx FPGAs, IEICE Electronics Express, Vol. 15, No. 10, pp. 20180386:1-20180386:12, 2018. DOI: 10.1587/elex.15.20180386
- [2] L. M. Reyneri, D. Del Corso, and B. Sacco: Oscillatory metastability in homogeneous and inhomogeneous flip-flops, IEEE Journal of Solid-State Circuits, Vol. 25, No. 1, pp. 254–264, 1990. DOI: 10.1109/4.50312
- [3] H. Hata and S. Ichikawa: FPGA Implementation of Metastability-based True Random Number Generator,” IEICE Transactions on Information and Systems, Vol. E95-D, No. 2, pp. 426–436, 2012. DOI: 10.1587/transinf.E95.D.426
- [4] N. Fujieda, H. Kishibe, and S. Ichikawa: A light-weight implementation of latch-based true random number generator, 15th International Wireless Communication and Mobile Computing Conference (IWCMC 2019), pp. 901-906, 2019. DOI: 10.1109/IWCMC.2019.8766516