DA コンバータがなくてもできる FPGA ピアノ (2)

前回の実装では FPGA から指定した周波数のパルス波を出力し、圧電スピーカーから音を出すことができるようになりました。あとは音階に対応した周波数を各ボタンスイッチに割り当てれば、だいぶピアノらしくなるはずです。いわば FPGA ピアノの調律の作業です。さて、ピアノの調律といえば音の高さだけではなく音色の調整も行います。そこで今回は簡易的な音色の調整機能として PWM (Pulse Width Modulation) のメカニズムを実装して、自由にパルス幅を変更できるようにしてみましょう。また、スピーカーやヘッドフォンなども鳴らせるように、ブレッドボードにアンプを実装して FPGA と接続してみます。

まずは音階と周波数の関係について確認するところから始めましょう。

FPGA ピアノを調律する

基準音の周波数

オーケストラのコンサートでは、指揮者が登場する前に舞台上でチューニング (音合わせ) をする習慣があります。まずオーボエ奏者が基準音を鳴らし、コンサートマスターがその音を引き継ぎ、それに各楽器が合わせていきます。ちょっとしたセレモニーのような感じでもあり、客席のワクワク度も膨らむ瞬間です。

このチューニングの基準音に使われるのが「ラ」の音です。ピアノの調律も、まずはこの音を合わせます。さて、この基準音の周波数、現在の国際標準では 440 Hz ということになっていますが、これが一筋縄では行きません。楽器を演奏される方はご存知かと思いますが、日本のオーケストラでは 440 Hz はむしろ少数派で、たいていは 442 Hz など少し高めの周波数が使われます。家庭用のピアノの調律も同様のようです。国によってもさまざまで、アメリカのオーケストラでは 440 Hz が一般的なのに対し、ヨーロッパでは 445 Hz を超えるかなり高い周波数が使われることもあるようです。

ほんの数 Hz の差ですが、音楽家にとってはかなり印象が異なるようです。一方、昔のチューニングはもっと低かったそうで、ピアノよりも歴史の古い鍵盤楽器のチェンバロは、現代でも 415 Hz でチューニングされることが多く、これは今のピアノに比べると半音低くなります。

筆者の手元の電子楽器では、438 Hz から 445 Hz を調整できるつまみがついており、購入時は 442 Hz に設定されていました。以下の設計例でも、基準音の周波数は定数パラメータとしていますので、お好みに応じて設定してください。

オクターヴと平均律

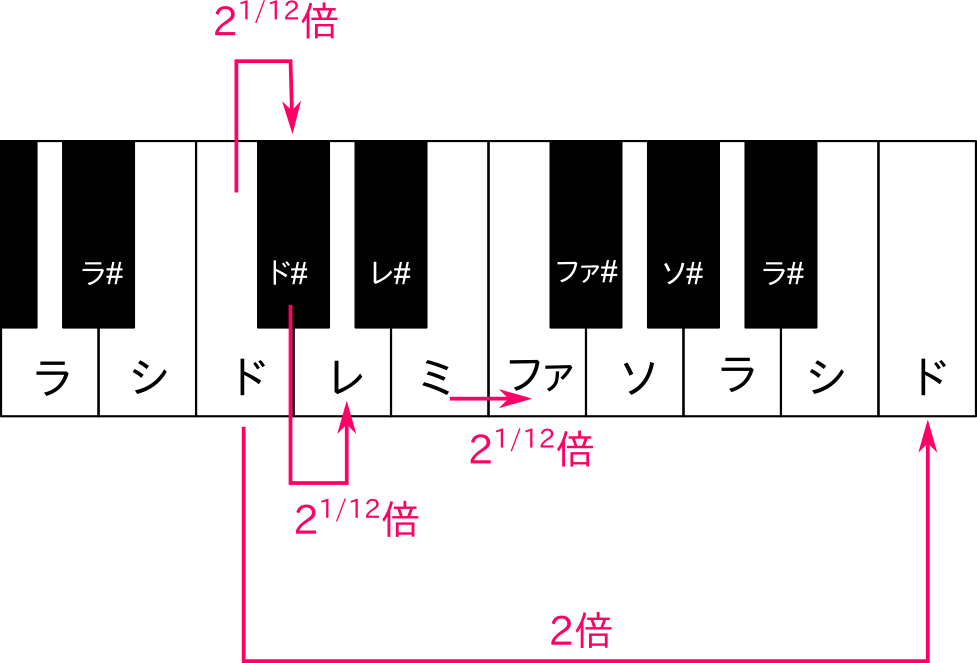
ピアノの白鍵を順に「ドレミファソラシド」と押していくと「ド」が2回出てきます。「低いド」と「高いド」ですね。この2つの「ド」の関係をオクターヴといい、これは周波数でいうとちょうど2倍の関係になります。たとえば基準音の「ラ」を 442 Hz でチューニングした場合、その音より1オクターヴ高い「ラ」の周波数は 884 Hz になります。反対に1オクターヴ低い「ラ」の周波数は 221 Hz になります。

さて、西洋音楽では1オクターヴを12音に分けて音階を構成します。ピアノの鍵盤を見ると分かりますが、1オクターヴの中に白鍵が7つ黒鍵が5つあり、合計で12音です。これらの音の周波数の決め方を音律といいます。これにもいろいろ種類があるのですが、ピアノでは平均律とよばれる音律が使われます。これは、隣り合う音 (半音) の周波数の比が一定となるように周波数を決める音律です。

たとえば「ド」と「ド♯」の周波数の比と「ド♯」と「レ」の周波数の比は同じです。つまり、半音階の周波数を順に並べると等比数列になります。12音で周波数が2倍になるのですから、公比は2の12乗根 ($ \sqrt[12]{2} $) です。したがって、「半音上」というのは、周波数でいうと$ \sqrt[12]{2}$倍ということになります。反対に、「半音下」は周波数でいえば$ \frac{1}{\sqrt[12]{2}}$倍のことです。指数で表せば、「半音上」が$2^{\frac{1}{12}}$倍、「半音下」が$2^{- \frac{1}{12}}$倍です。

平均律はハモらない?

このように、平均律は12音の周波数を対数軸上で等間隔になるように並べた音律です。数学的には明解ですが、どの2つの音を選んでも、オクターヴ以外の場合は、その周波数の比は無理数になります。実はこれが困ったことなのです。

2つの音が同時に鳴ったとき、きれいに調和して聴こえるのは、それらの周波数が簡単な整数の比で表されるときです。2つの波の位相がよく揃い、不快なうなりが生じないからです。しかし、無理数は整数比では表せません。つまり平均律ではオクターヴ以外の音は完全には調和しないのです。実際、動的に周波数を調整できる弦楽器や声楽のアンサンブルでは、平均律とは異なる音律で演奏されることが多いようです。

しかし、音階の周波数が等間隔でないと、調性が変わるたびに各音の周波数を変えないといけません。ピアノはそのようなことは簡単にはできませんので、どんな調性の曲でも自由に演奏できるように平均律が用いられるのです。

さらにいうと、1オクターヴは周波数が2倍というのも絶対ではありません。高音域や低音域では、人が美しいオクターヴと感じる周波数の比は2倍からずれるのだそうです。優れた調律師が調整したピアノでは、高音域や低音域のオクターヴの周波数比はぴったり2倍にはなっていないそうです。

音程とカウンタの増分値

かように音の世界は奥深いのですが、あまり深入りするとややこしいので、ここは割りって基準音に$2^{\frac{1}{12}}$の冪を乗じる平均律で音階を調律することにしましょう。まず、対象音と基準音の距離を符号つき整数 $n$ で表すことにします。コーディングを簡単にするため、楽典に出ててくる「音程」とは異なる定義を採用し、半音を1と数えることとします。また、符号がプラスのときは高い方向への距離、マイナスは低い方向への距離とします。 $n = 0$ ならば同じ音、$n = 12$ なら1オクターヴ上の音、$n = -12$ なら1オクターヴ下の音です。

基準音の周波数を $f_b$ とすると、そこからの距離が $n$ の音の周波数は$$f_p = 2^{\frac{n}{12}} \cdot f_b$$と表せます。周波数さえ分かればカウンタの増分値を計算してその音を鳴らすことができます。前回も出てきた式ですが、クロックの周波数を $f_c$、カウンタのビット幅を $w$ とすると、周波数 $f_p$ のパルスを出力するためのカウンタの増分値は$$i = \frac{2^w}{f_c}f_p$$と書けるのでした。ここに先ほどの式を代入すれば$$i = 2^{(w+\frac{n}{12}) } \frac{f_b}{f_c}$$が得られます。この関係を使えば、前回の設計に少しだけ変更を加えることで音階を鳴らすことができます。

ソースコードの変更点

前回は周波数からカウンタの増分値を求める関数 freq2inc を使って、各ボタンに対応するカウンタの増分値を事前計算していました。今回は、基準音からの符号付き距離 $n$ を引数としてカウンタの増分値を計算する関数 n2inc を用意します。

function bit [COUNT_WIDTH-1:0] n2inc(int n);
  return ((2.0 ** (COUNT_WIDTH + n / 12.0)) * BASE_FREQ / CLK_FREQ);
endfunction

先ほどの式そのものですね。ここで BASE_FREQ は基準周波数のパラメータで、442 Hz なら

localparam real BASE_FREQ = 442.0;

などとしておきます。あとは、各ボタンと $n$ を関係づければ OK です。Arty には4つのボタンがありますので、それぞれ「ド」「レ」「ミ」「ファ」の音に対応させることにします。すると対応する $n$ は、それぞれ$-9, -7, -5, -4$になります。そこで、各ボタンに対応するカウンタの増分値を格納する配列 INCS の記述を

localparam bit [COUNT_WIDTH-1:0] INCS[4] = '{
  n2inc(-4), n2inc(-5), n2inc(-7), n2inc(-9)
};

のように変更します。Arty の4つのボタンは、右から順番に0番から3番まで並んでいるのですが、ピアノの鍵盤は左の方ほど低い音になっていますので、$n$ の値を逆順に書いています。

修正点はたったこれだけです。ぜひ実機で試してみ下さい。無事に「ド」「レ」「ミ」「ファ」が鳴りましたか? 音階が出るだけで、ぐっと楽器らしくなったと思います。4音だけなのが少し物足りないですが、Arty では RESET のボタンも使えますので「ソ」まではいけます。後はスライドスイッチと組み合わせて…と色々工夫してみてください。

PWM による音色の変更

ピアノの調律は音の高さを調整するだけではありません。音色の調整も行います。ここまではパルス波によって音を出してきましたが、この音色を変える簡単な方法があります。

PWM 波形生成の原理

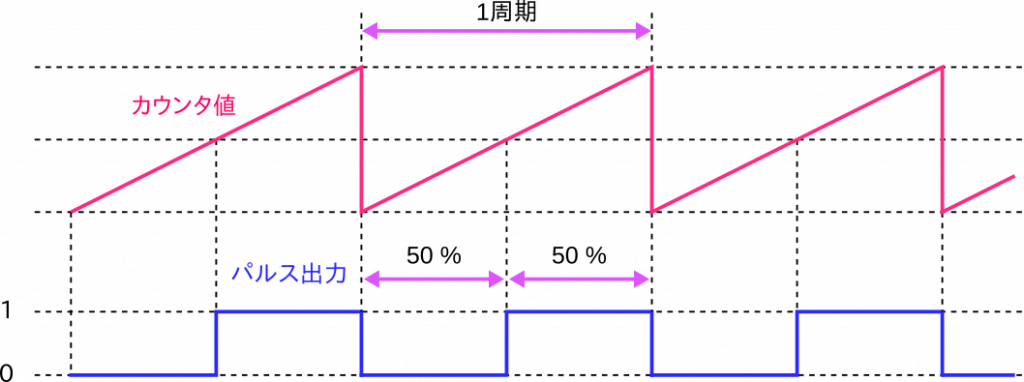
パルス波出力のメカニズムをおさらいすると、カウンタの MSB をそのまま出力していますので、周期の前半は0が出力され、後半は1が出力されます。したがって、1が出力される期間の長さと0が出力される期間の長さは同じです。カウンタの増分値が周期を割り切れなかったりすると、厳密にはちょっとずれが生じますが、それでもほとんど同じと考えてよいでしょう。これをデューティ比が 50% のパルス波といいます。

このデューティ比を変更できるようにしてみましょう。たとえば 25% と設定すると、1周期の1/4の期間が1になり、残りの期間は0となるといった具合です。パルス波のデューティを変更するというのは、LED の明るさ、モーター、スイッチング電源の制御などでもお馴染みの PWM (Pulse Width Modulation: パルス幅変調) と同じです。もっとも、今回は変調というほど頻繁にデューティ比を変更するわけではありませんが、原理は同じです。

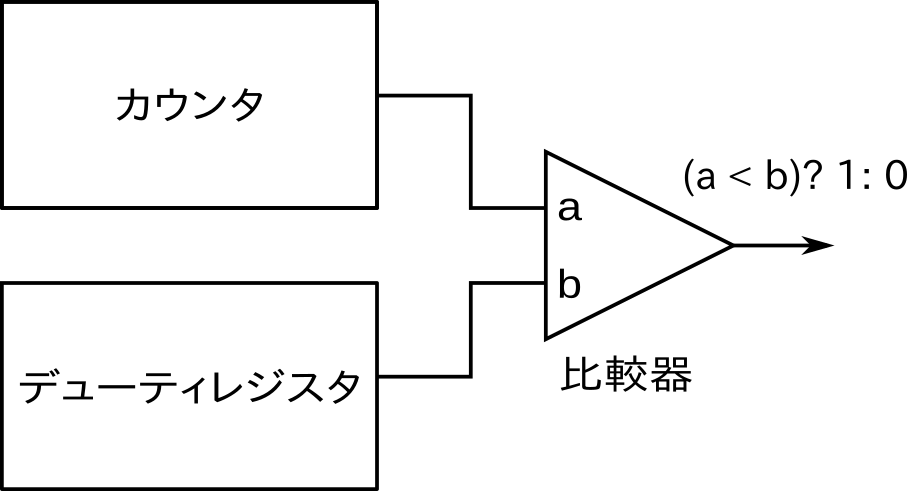
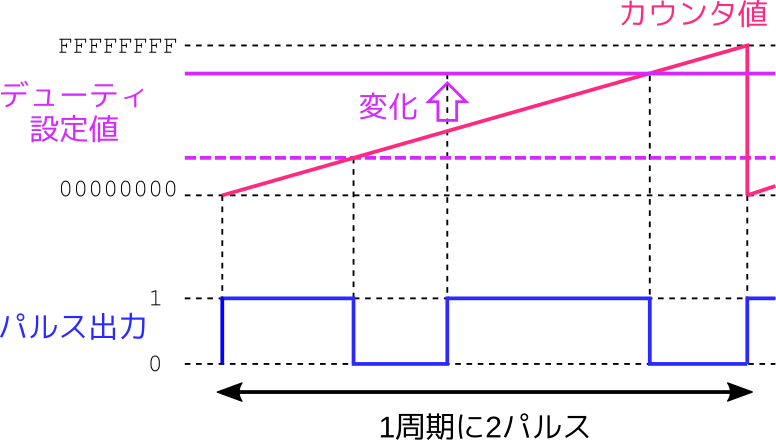
PWM になってもパルスの周期をカウンタで制御する部分は変わりません。変更するのは出力信号を生成する部分です。まず、デューティ比の設定値を保存しておくレジスタを作ります。これをデューティレジスタと呼ぶことにします。次に、現在のカウンタの値とデューティレジスタの値を比べる比較器を追加します。この比較器はカウンタ値がデューティレジスタの値未満であれば1、そうでなければ0を出力します。

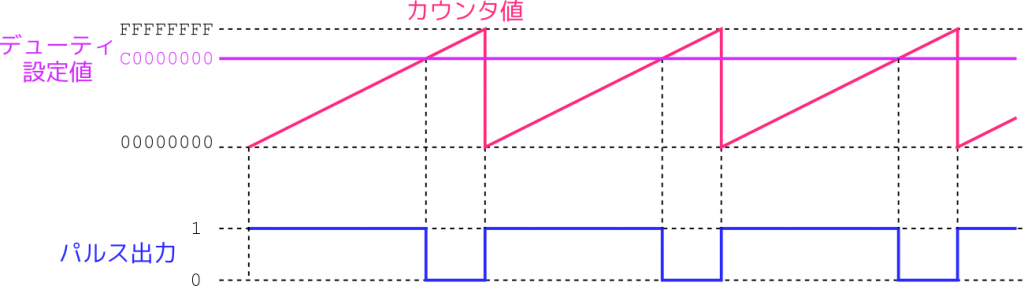
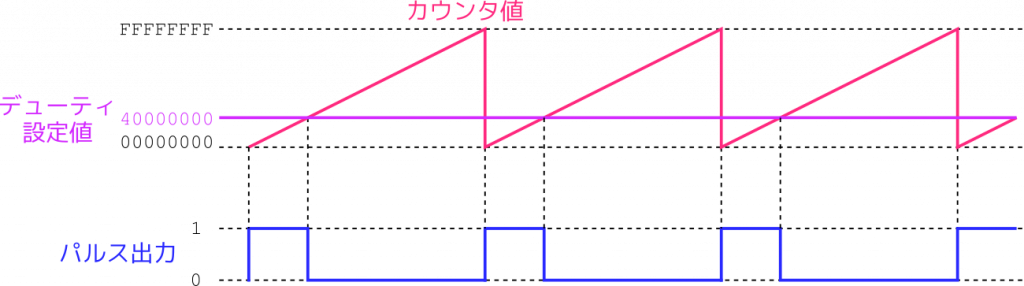
動作を具体例で考えてみましょう。32ビットのカウンタに対して、デューティレジスタに16進数のC0000000を設定したとします。カウンタ値がC0000000未満なら1が出力され、C0000000以上なら0が出力されます。すると次の図のようにデューティ比が75%のパルスになります。これは $2^{32} \times 0.75 = \mathrm{C0000000}_{(16)}$ の関係が成り立つからです。

次にデューティレジスタの値を減らして、16進数の40000000にしてみます。するとカウンタは先ほどよりも早く設定値に到達しますので、1を出力する期間はそれだけ短くなります。$2^{32} \times 0.25 = \mathrm{40000000}_{(16)}$ が成り立つので、出力パルスのデューティ比は 25% になります。

デューティレジスタに0を設定すると、カウンタが0未満の値を取ることはないのでパルス出力は0に固定されます。デューティ比0%です。

最大値を設定したらどうなるでしょうか。デューティレジスタのビット幅がカウンタと同じ32ビットならば、設定可能な最大値は16進数のFFFFFFFFです。当然カウンタの最大値と同じです。というわけで、カウンタ値がこの値をとった瞬間はパルス出力は0になります。つまりデューティ比が完全に 100% にはなりません。どうしても 100% を設定する必要がある場合には、デューティレジスタのビット幅を33ビットにする必要があります。

PWM 出力のための比較器を SystemVerilog で書いてみましょう。

always @(posedge clk) begin
  if (btn_in != '0 && count < duty_reg)
    pulse_out <= 1'b1;
  else
    pulse_out <= 1'b0;
end

これも簡単ですね。duty_reg がデューティレジスタです。if には条件が2つ記述されています。1つ目の条件は、そもそもどのボタンも押されていないときには PWM 出力を0に固定するためのものです。2つ目の条件が、設定されたデューティ比のパルスを出力するためのものです。

ところで、何気なく示したこのコードですが、always @(posedge clk) を使った順序回路の記述になっているのにお気づきになったでしょうか。つまり1ビットのフリップフロップが合成されるようになっています。比較器は組み合わせ回路なのだから、always_comb としても良さそうなものです。そうなっていないのは、もちろん理由があるのです。

グリッチの罠

組み合わせ回路の出力を、そのまま外部に出力すると思わぬ落とし穴にはまる危険があります。その原因は論理ゲートや配線の遅延時間です。

通常、ハードウェアの論理設計の段階では、入力の変化が出力を変化させるまでの遅延時間については細かく考えません。HDL 記述を RTL シミュレーションする場合も、組み合わせ回路の部分は遅延がないものとして扱われます。もちろん、このこと自体は悪いことではありません。開発の生産性向上には、抽象度の高い設計が欠かせません。しかし、抽象度を上げることによって、何を切り捨てたのかを理解しておくことも時には重要になります。

さきほどの比較器の例を always_comb を使って組み合わせ回路として記述してみると、RTL シミュレーションでは全く問題なく動作します。そこで Vivado で FPGA に実装し、実装後のネットリストを用いて遅延付きのゲートレベルシミュレーションを行ってみました。

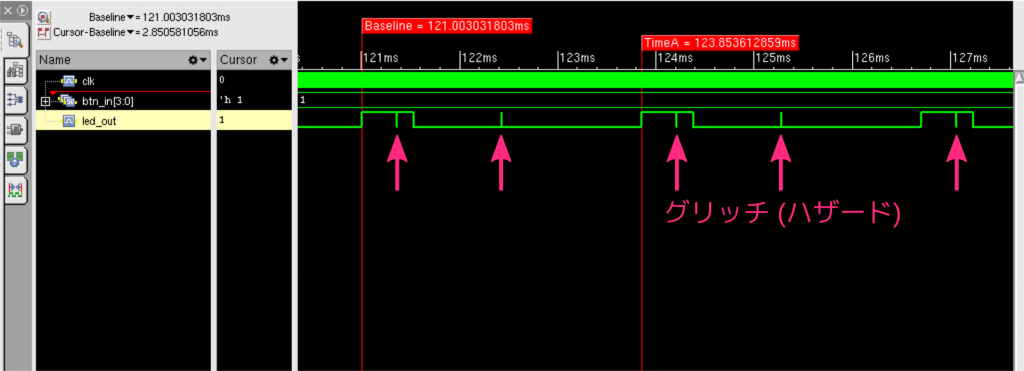
波形を見ると分かるように、本来1が継続的に出力されるべき区間や、0が継続的に出力されるべき区間にノイズのような出力が表れています。これがグリッチと呼ばれる現象です (ハザードということもあります)。このような出力をしてしまうと、たとえば、外部回路がパルスの回数を数えるようなアプリケーションなら完全に誤動作してしまいます。

厄介なことに、この現象は遅延を考慮しない RTL シミュレーションでは現れません。また、遅延時間はデバイスの特性のばらつきや温度への依存もありますので、必ずこのようなタイミングで生じるというわけでもありません。

グリッチの発生メカニズム

なぜこのようなことが起きるのか、そのメカニズムを考えてみます。簡単のため、カウンタとデューティレジスタは3ビット幅とし、デューティレジスタには6が設定されているとします。ここで、カウンタ値が3から4に遷移するときのことを考えてみましょう。

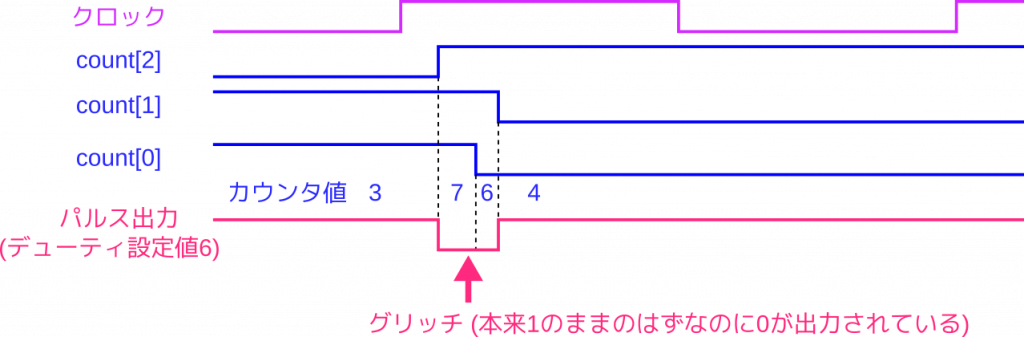
カウンタ値の3から4へ遷移というのは、2進数で考えると011から100への遷移ということになります。3ビットのカウンタのすべてのビットが変化することになりますが、クロックが立ち上がってから各ビットが変化するまでの遅延時間はばらばらです。次のタイミングチャートでは count[2] が最も早く変化し、次に count[0]、最後に count[1] が変化した例を示しています。

この例ではカウンタ値は3から4へ直接遷移するのではなく、瞬間的には7や6の値を経由することになります。3と4はデューティレジスタの設定値である6未満の値ですので、論理的には3から4への遷移の際にパルス出力は1のまま変化しないはずです。しかし、遷移の途中で7や6を経由してしまうと、これは6未満ではないので、一時的に0が出力されることになります。論理的には生じないはずの出力信号の変化が、遅延時間のずれの関係で生じるのです。これがグリッチの正体です。

では、どうすればよいのか

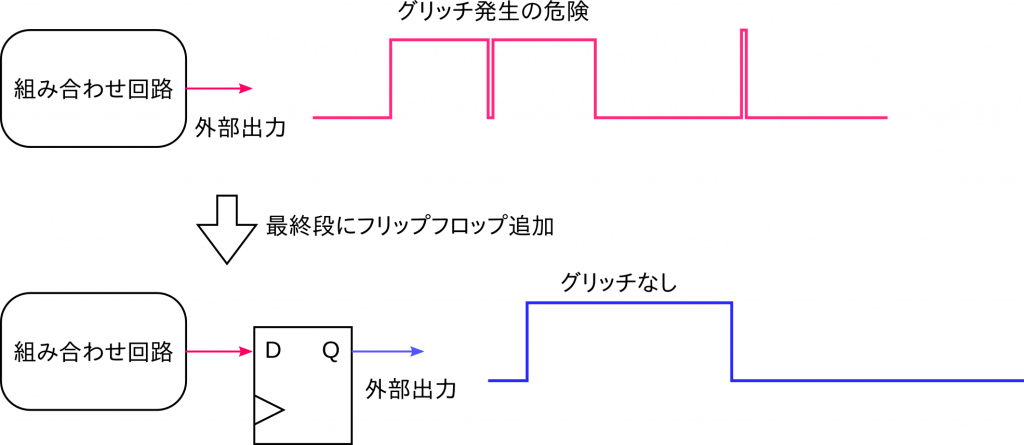
グリッチ発生の原理が分かったところで、その対象法を考えましょう。問題の本質は、クロックが立ち上がってから、組み合わせ回路の出力が最終的な値に落ち着くまでの間に、ゲートや配線の遅延時間の関係で出力がばたつくことでした。ですから、もっとも簡単な対処法は落ち着くまで待ってからその値を使うことです。そのためには、組み合わせ回路の出力をフリップフロップで受けてから外部に出せばよいのです。これが、さきほどの例で比較器の論理を always @(posedge clk) で記述した理由です。

この方法は確実ですが、信号が外部に出力されるのが1クロック遅くなります。たいていの場合は、1クロックくらい遅くなってもどうってことはありませんが、どうしても嫌なら別の方法を考える必要があります。いつでも使える手ではありませんが、組み合わせ回路の構成をわざと冗長にしてグリッチが出ないようにするテクニックもあります。興味のある方はディジタル回路設計とコンピュータアーキテクチャなどの専門書をご覧下さい。

デューティレジスタの更新タイミングにも注意

PWM で本格的にパルス幅変調をかける場合には、デューティ比の設定値が刻々と変化することになります。このときに気をつけたいのが、デューティレジスタの更新タイミングです。パルスを出している最中にレジスタを更新してしまうと、次の図のように1周期の中に2回以上パルスが出てしまなどのイレギュラが生じる可能性があります。

このようなことが問題になるかどうかはアプリケーションにもよりますが、問題になる場合には、デューティレジスタの更新は1周期に1回だけ周期の先頭で行う、などのタイミング制御が必要になります。

今回の設計ではそう頻繁にデューティ比を変更するわけではないので、あまり神経質に考える必要はありませんが、音を出している最中はパルス幅は変更できないようにします。つまり、どのボタンも押されていないとき (パルス波出力が止まっているとき) に限って、デューティレジスタを更新します。設定値は Arty に搭載されている4つのスライドスイッチを使って、デューティレジスタの上位4ビットを直接設定するようにします。下位28ビットは常に0です。SystemVerilog の記述例を示します。

always @(posedge clk) begin
  if (btn_in == '0)
    duty_reg[(COUNT_WIDTH-1)-:4] <= sw_in;
end

sw_in が4ビットのスライドスイッチ入力です。if 文はどのボタンも押されていないことをチェックするためのものです。音を出していないときには、スライドスイッチの入力がデューティレジスタの上位4ビットに毎クロック格納されます。

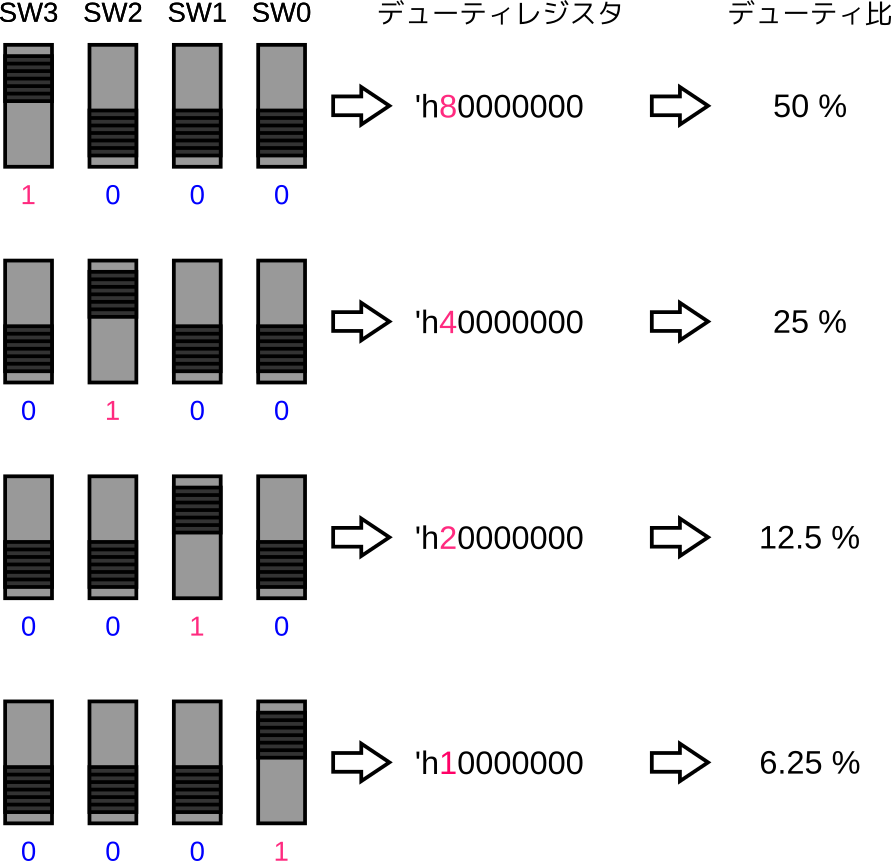
デューティ比の設定例

デューティ比設定の具体例を次の図に示します。4つのスライドスイッチのうち、左端のスイッチ (SW3) だけを ON (上側) にすると、2進数の1000がデューティレジスタの上位4ビットに設定されますので、16進数では80000000となります。$\frac{80000000_{(16)}}{2^{32}} = 0.5 $ より、これはデューティ比 50% を設定したことになります。

同様に左から2番目のスイッチ (SW2) だけを ON にすると、デューティ比として25%を指定したことになります。Arty はスイッチが少ないため、このようにちょっと強引な仕組みにしました。FPGA をもっと活用するために IP コアを使ってみよう (2) で説明されている VIO (Virtual I/O) を使えば、32ビットのデューティレジスタに自由に値を設定できるようになります。ぜひトライしてみてください。

SystemVerilog コードを完成させる

断片的に説明してきましたが、これで SystemVerilog のコードは一通り完成しました。まとめると、こんな感じです。

`default_nettype none

module pwm_sound
  #(
    parameter real CLK_FREQ = 100e6, // クロック周波数 (Hz)
    parameter int  COUNT_WIDTH = 32  // カウンタビット幅
  )
  (
    input wire 	     clk,
    input wire [3:0] btn_in, // ボタン入力
    input wire [3:0] sw_in,  // スライドスイッチ入力
    output logic     led_out,
    output logic     pulse_out = 1'b0
  );

  localparam real BASE_FREQ = 442.0;            // 基準音の周波数
  localparam bit [COUNT_WIDTH-1:0] INCS[4] = '{ // カウンタの増分値
    n2inc(-4), n2inc(-5), n2inc(-7), n2inc(-9)  // ファ，ミ，レ，ド
  };

  logic [COUNT_WIDTH-1:0] count = '0;    // カウンタ
  logic [COUNT_WIDTH-1:0] duty_reg = '0; // デューティレジスタ

  always @(posedge clk) begin 
    if (btn_in == '0)
      count <= '0; // どのボタンも押されていなければカウンタをクリア
    else begin
      for (int i = 0; i < 4; i++) begin
        if (btn_in[i]) begin
          count <= count + INCS[i]; // 押されたボタンに対応する増分値を加える 
          break;
        end
      end
    end
  end 

  always @(posedge clk) begin 
    if (btn_in == '0) // どのボタンも押されていないときだけ
      duty_reg[(COUNT_WIDTH-1)-:4] <= sw_in; // 上位4ビットを更新
  end

  always @(posedge clk) begin 
    if (btn_in != '0 && count < duty_reg) // PWM 発生用の比較器
      pulse_out <= 1'b1;
    else
      pulse_out <= 1'b0;
  end

  assign led_out = pulse_out; // 確認用 LED 出力

  // 基準音の距離からカウンタの増分値を計算する関数
  function bit [COUNT_WIDTH-1:0] n2inc(int n);
    return ((2.0 ** (COUNT_WIDTH + n / 12.0)) * BASE_FREQ / CLK_FREQ);
  endfunction 
endmodule

`default_nettype wire

トップモジュールやArty A7-35T 用の IO ピン割り当てファイルを含むソースコードは Gist からダウンロードできます。モジュール名を変更して pwm_sound としました。入出力は前回の設計とほぼ同じですが、スライドスイッチ入力のため4ビットの sw_in が加わりました。PWM 出力の pulse_out は、前回と同じく Pmod JA の1番ピンを使うことを想定しています。

改めて見ると前回のソースコードとそれほど大幅には変わっていません。特に24行目から35行目のカウンタの記述はまったく一緒です。例によって確認のためにパルス波の信号を LED にも出力するようにしています。パルス幅を変更すると、LED の明るさが変わるのが確認できるはずです。

以下が簡単な RTL シミュレーションの結果です。スライドスイッチ sw_in の設定を変えることでパルスのデューティ比が 50% から 25% になっていることが確認できます。

そもそもデューティ比を変えるとなぜ音色が変わるのか?

これを説明していませんでした。デューティ比を変えると何が変わるのでしょう。もちろんパルス幅です。しかし、異なった見方もできます。世の中のすべての波形は、さまざまな周波数や位相の正弦波を足し合わせることで作り出すことができます。フーリエ変換の原理ですね。

パルス波の周波数スペクトラム

それではパルス波はどのような正弦波の組み合わせなのでしょうか。数式で考えても良いのですが、視覚的に見た方がイメージしやすいですね。こういうときは Python が便利です。

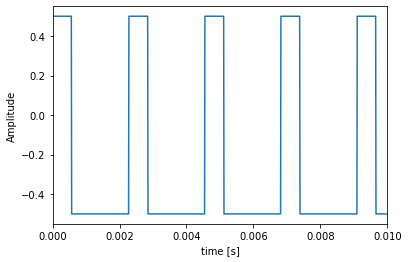
周波数 440 Hz でデューティ比が50 %のパルス波を1秒間分作ってみます。解析上のサンプリング周波数は 100 KHz としています。

fp = 440     # パルス周波数 (Hz)
fs = 100000  # サンプリング周波数 (Hz)
duty = 0.5   # パルスデューティ 
T = 1        # 解析時間 (秒)

t = np.linspace(0, T, T * fs, endpoint=False)
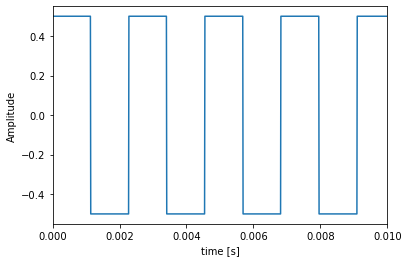
x = np.floor(t * fp) - np.floor(t * fp - duty) - 0.5

Jupyter Notebook のファイルは Gist にありますので、ぜひ手元でお試しください。これを時間軸でプロットするとこんな感じです。振幅は -0.5 から +0.5 まで振らせています。

Numpy の FFT を使うと簡単にフーリエ変換することができます。

X = np.fft.fft(x)
freqs = np.fft.fftfreq(len(x)) * fs

X に変換結果が入ります。freqs は周波数領域のインデックスを実際の周波数に変換したものが入ります。これをプロットすると周波数スペクトラムが得られます。

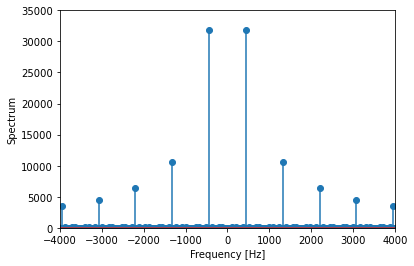
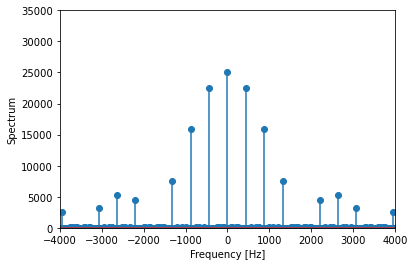
マイナスの周波数が出てきますが、フーリエ変換では複素数を cos と sin に対応させ、セットで位相を表すからです。今回の例では周波数領域で左右対称ですから、あまり気にせずプラスの周波数だけを見ても構いません。

まず、一番高いピークがパルスの周波数である 440 Hz に来ています。これは当然ですね。次にその3倍の1320 Hzにもピークがあり、この周波数成分も含まれていることがわかります。3次高調波です。さらに5倍の2200 Hz にももう少し低いピークがあります。7倍の3080 Hz の成分も含まれることがわかります。グラフの領域からは出てしまいますが、さらにその上の9倍、11倍のところにもピークが見られます。このようにデューティ比 50% のパルス波には奇数倍の高調波が含まれ、高いものほどその強度は小さくなっていくという特徴があります。

音色の正体

実は我々が「音色」と感じるのは、この高調波の含まれ具合なのです。物理的には異なる周波数の正弦波の音が同時に鳴っているのですが、我々はそれを異なる音とは認識せずに、まとめて1つの音として認識しているのです。その代わり、どのような高調波がどの程度の割合で混じっているのかを「音色」として感じるということなのです。

それでは周波数は変えずに、デューティ比だけを変えたパルス波で見てみましょう。さきほどの Python コードで duty を0.25とするだけでデューティ比 25% のパルス波を作れます。

これをフーリエ変換し、周波数領域でプロットするとこんな感じです。

さきほどと異なり、偶数次の高調波 (例えば 880 Hz) も出てきました。また、必ずしも周波数の高い高調波ほど強度が低くなっているわけでもありません。たとえば6次の高調波 (2640 Hz) は5次 (2200 Hz) のものより強く現れています。なお、周波数が 0 Hz の直流成分も出ています。これはデューティ比が25 %になったことで、パルスの0の区間と1の区間の長さが等しくなくなり、パルス振幅の平均値が0ではなくなったためです。

パルスのデューティ比を変えることで高調波の混じり具合が変わり、それが人の耳には音色の変化として認識されるということなのです。

スピーカーを鳴らす

さて、さまざまな音をさまざまな音色で奏でられるようになってくると、いよいよ圧電スピーカーでは物足りなくなってきます。とても手軽で便利な素子でしたが、幅広い周波数の音を発するのには向いていません。圧電スピーカーにはここでお別れすることにして、スピーカーやヘッドフォンを鳴らせるようにしてみましょう。

前回も説明したように、スピーカーやヘッドフォンを駆動する電流を FPGA からダイレクトに取るのは無理があります。そこで必要になるのが信号を増幅するアンプです。手っ取り早くアンプつきのスピーカーを用意するとか、アンプのキットを用意するとかでも良いのですが、せっかくなのでブレッドボードを使って自作してみます。

アンプの回路

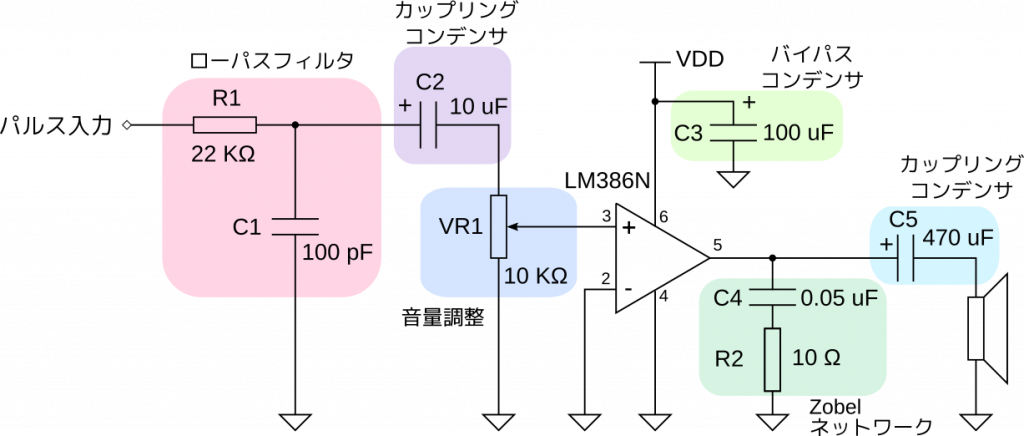
今回は低電圧オーディオアンプ IC として定番の LM386 を使います。推奨電源電圧は4 V から12 V で、6 V で動作させた際の静止時消費電力はわずか24 mW と乾電池でも十分です。作成したアンプの回路図を示します。

Texas Instruments の LM386 のデータシートに掲載されている最小部品回路構成例を参考にしています。各部の機能を簡単に説明します。

ローパスフィルタ

R1 と C1 は入力信号から高周波成分を除去するローパスフィルタです。スピーカーを鳴らすためだけならば無くても構わないのですが、次回以降にちょっと使いたいため付けました。

抵抗値を $R$、容量を $C$とするとローパスフィルタのカットオフ周波数は、$$ f_c = \frac{1}{2 \pi RC} $$で計算できます。今回は 22 KΩ と 100 pF ですので、約 72 KHz となり、これより高い周波数の成分は減衰します。可聴周波数よりもだいぶ高い帯域です。カットオフ周波数というと、ここを境にスパッと信号がカットされるイメージを持たれるかもしれませんが、実際には RC フィルタの周波数特性は急峻ではありません。また、前回も触れましたが、Arty の Pmod JA には保護用の 200 Ω 抵抗がついていますので、実質の $R$ は 22.2 KΩ となり、カットオフ周波数ももう少し低くなります。

入力カップリングコンデンサと音量調整用可変抵抗

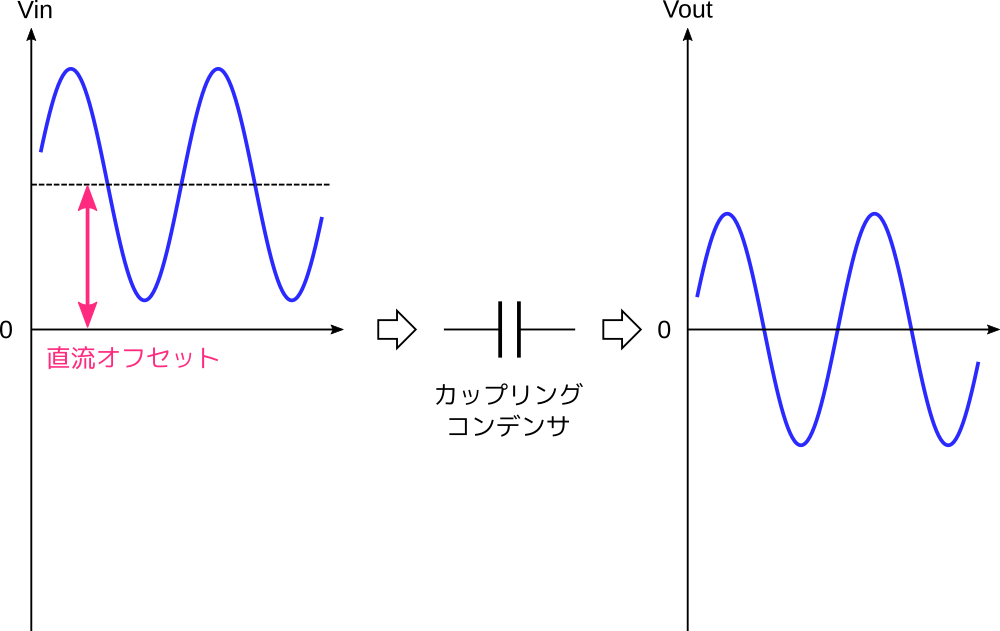
コンデンサには交流は通すが直流は遮断するという性質があります。この性質を利用すると、次の図のように信号の直流オフセットを除去することができます。このような目的で使うコンデンサのことをカップリングコンデンサといいます。

C2 はローパスフィルタを通過した信号から直流成分を除去するカップリングコンデンサです。VR1 は音量調整用の可変抵抗で、アンプに入力される信号の振幅を調整します。10 KΩ の値はデータシートの回路構成例と同じにしています。ここまでがアンプに対するフロントエンドです。

バイパスコンデンサ

C3 は LM386 への電源供給ラインからノイズを除去するバイパスコンデンサです。略してパスコンとも呼ばれます。これも交流は通して直流は遮断するというコンデンサの性質を利用しており、電源電圧に生じたノイズ成分を GND に逃すことで LM386 へ供給電圧を安定させる働きがあります。アンプは一種のフィードバックシステムですので、ちょっとバランスが崩れるとすぐに発振してしまいます。特に LM386 は電源電圧の振動に弱いようです。このコンデンサはデータシートの回路構成例では記載されていませんが、筆者の環境ではこのパスコンを入れないと発振してしまいました。

Zobel ネットワーク

C4 と R2 はZobel ネットワークと呼ばれる回路です。スピーカーのインピーダンスは周波数によって大きく変化してしまうのですが、それを補償する働きがあり、アンプの安定性に寄与します。定数はデータシートの回路構成例のものをそのまま使っています。

出力カップリングコンデンサ

C5 は最終的な出力信号から直流オフセットを取り除くカップリングコンデンサです。スピーカーのインピーダンスと合わせてハイパスフィルタとして働きます。ハイパスフィルタのカットオフ周波数も$$ f_c = \frac{1}{2 \pi RC} $$と計算できます。

データシートの回路構成例ではこのコンデンサの値は 250 uF となっており、スピーカーのインピーダンスを 8 Ω とするとカットオフ周波数は約80 Hz になります。少し高い気もしたので、手元にあった470 uF を使ってカットオフ周波数が約42 Hz になるように変更しました。

フロントエンドの電子回路シミュレーション

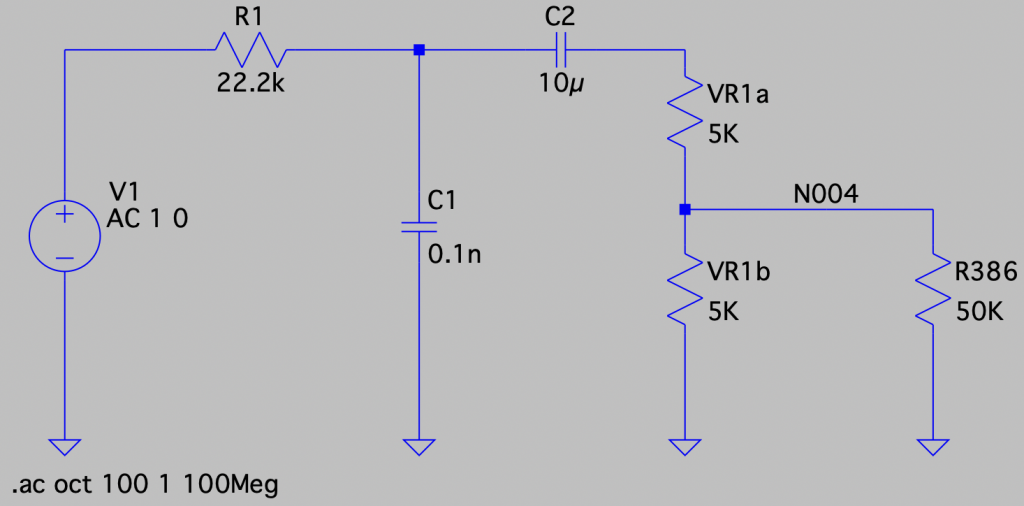
というわけで、今回のアンプ回路はほぼデータシートのお手本どおりなのですが、フロントエンドは変更していますので、念のためシミュレーションで動作を確認してみます。シミュレーションには Analog Devices から無償提供されている LTspice を使いました。

データシートによれば LM386 の入力インピーダンスは 50 KΩ です。可変抵抗をちょうど真ん中に設定したとして、次のようにシミュレーション回路を作成しました。R1 は Arty の Pmod JA コネクタのオンボード抵抗も含めて 22.2k としています。

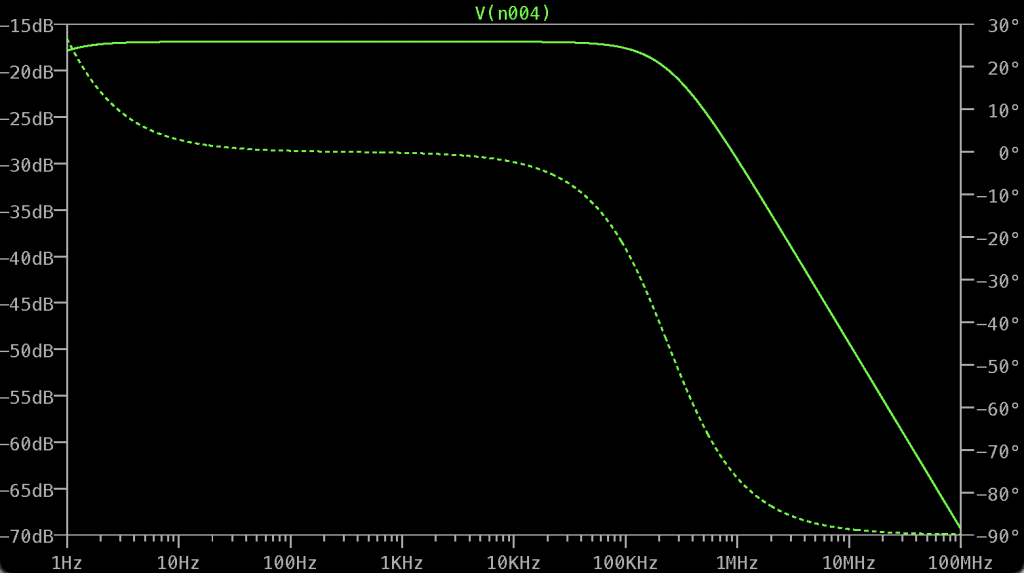
それではシミュレーション結果を見てみましょう。LM386 への入力信号となる N004 の接点の周波数特性をプロットしてみましょう。

実線が振幅特性、点線が位相特性です。可変抵抗で半分に分圧しているため全体的に減衰していますが、概ね意図した特性が実現できていることが確認できます。

ブレッドボードへの実装と FPGA との接続

注意!! アンプにはヘッドフォンやイヤフォンも接続できますが、意図せず大音量が出る可能性があります。耳を痛めないよう、ヘッドフォンやイヤフォンは決して耳には付けず、耳から離して実験してください。

アンプ回路をブレッドボードに実装した例を示します。C3 のパスコンはなるべく LM386 の近くに配置するとよいでしょう。今回はイヤフォンなども簡単に接続できるよう、出力端子にはブレッド用の 3.5 mm オーディオミニジャックを付けてみました。

電源は乾電池4本を直列にして 6 V を供給してもいいですし、FPGA にちょうどよい電源供給ピンがあれば、それを使うこともできます。Pmod にも電源供給ピンがありますが、これは電圧が 3.3 V ですのでちょっと足りません。Arty の場合には Arduino シールドコネクタに 5 V 電源の供給ピンがありますので、これを使うことは可能です。

乾電池を使った接続例を示します。乾電池のプラス極とマイナス極をそれぞれブレッドボードに接続します。FPGA から出力されるパルス信号は、ブレッドボード上の R1 のところに接続します。ここまではいいのですが、FPGA の GND とブレッドボードの GND を接続するのを忘れてしまう人がたまにいますので注意してください。

電気系の方はまさかと思われるかもしれませんが、実際、ある学生さんから「なぜ繋がないといけないのですか?」と真顔で質問された経験が筆者にはあります。これには教育カリキュラムの問題もあるのですが、情報系の科目では信号伝送を1本の線で表す抽象化された図面ばかり出てくるので、流れ出た電流は必ず戻ってこなければならないという「回路」の基本をつい忘れてしまうようなのです。

とはいえ、忘れていたらなら思い出せばよいだけのこと。IoT やサイバーフィジカルシステムなど、FPGA ボードにセンサやアクチュエータなど外部回路を繋ぐ機会も多いと思いますが、GND 接続には注意しましょう。ということでいよいよ実機動作の確認です。

実機動作確認

ブレッドボードアンプに電子工作用のスピーカーを接続してみました。動作の様子を以下に示します。アンプの電源は Arty から 5 V を供給しています。パルスのデューティ比は 50%、25%、12.5%、6.25% の4パターンとして音階の鳴動を確認しています。音色が変化するのを聴きとれましたか? デューティ比に応じて確認用 LED の明るさが変化しているのも確認できたと思います。

FPGA を使った PWM 信号による音階

デューティ比をいろいろと変更して、テクノポップ調のサウンドや、昭和のテレビゲームを彷彿とするサウンドなど面白い音色を発見してみてください。

今回のアンプ回路は、とりあえず鳴れば良いといった程度のもので、雑音を抑えたり、音質を追求したりすると、もちろん奥が深いです。LM386 を使ったアンプの作成例はたくさん公開されていますので、それらを参考に改良してみるのも面白いと思います。

まとめ

平均律では音階の周波数は等比数列である
カウンタと比較器で PWM 信号を生成できる
パルスのデューティ比を変えると高調波のスペクトラムが変わる
音色は高調波のスペクトラムである
組み合わせ回路の信号を直接外部に出すのは危険
アンプの自作もそんなに難しくない
GND 接続は忘れずに

さてパルスの周期やデューティ比は自由に操れるようになりました。残るは振幅です。でも出力信号は1ビットだけ。次回はデルタシグマ変調でこの問題に取り組みます。

長崎大学・柴田裕一郎

2025年1月
月	火	水	木	金	土	日
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31

2025年1月
月	火	水	木	金	土	日
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31