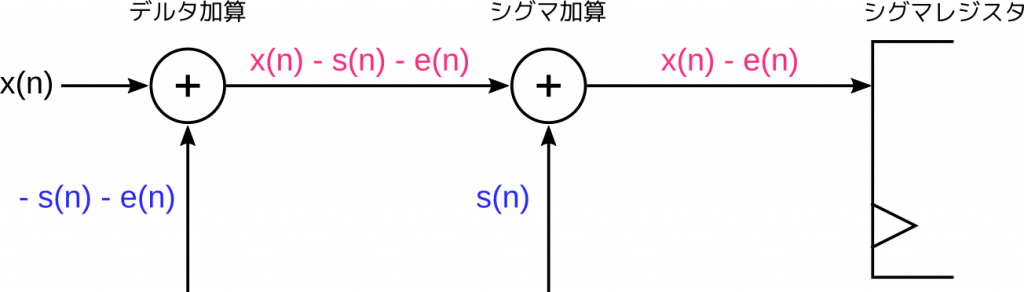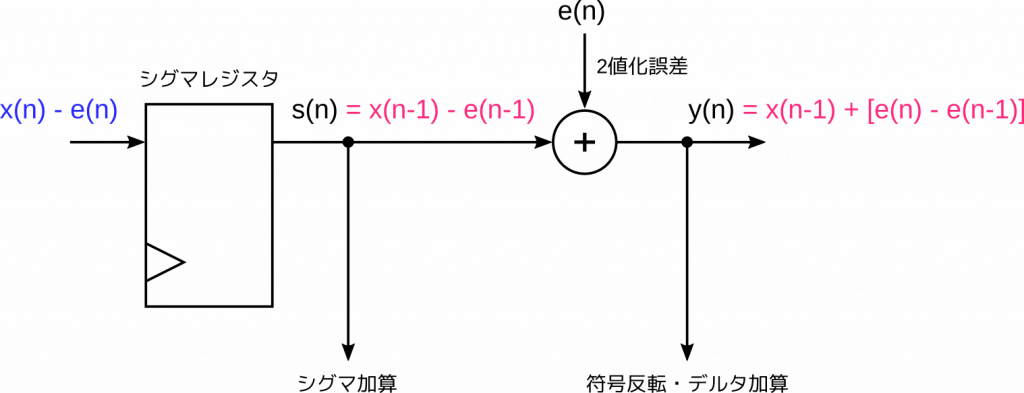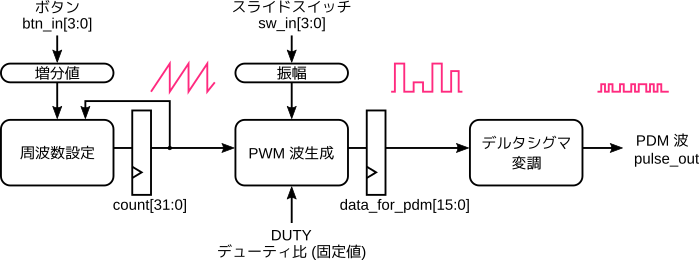今回は1ビットのディジタル出力を使ってアナログ信号を作り出すデルタシグマ型の DA コンバータを FPGA で実装します。これによってパルス波の振幅を変えることで前回作ったピアノの音量を調整してみます。デルタシグマって聞いたことはあるけど理論が何だか難しそう、というイメージをお持ちの方もいらっしゃるかもしれません。でも、そんなことはありません。Z 変換ができなくても大丈夫、基本原理はちゃんと理解できます。大部分の処理をディジタルで行うので FPGA 実装に向いていますし、回路構造もとても単純です。実際に作って動かしてみると、単純なのに賢いことがよく分かり、きっと愛着が湧いてきますよ。
アナログとディジタルのあいだ
前回の実装では平均律の音階の周波数に合わせてパルス波を発生させました。また、PWM (Pulse Width Modulation: パルス幅変調) でパルスのオン幅を変えられるようにし、音色も調整できるようにしました。1ビットのパルス波の周波数やオン幅を自由に操れるようになったわけです。さらにその振幅も変えたいというのが今回のテーマです。
つまり、0か1しか出力できない1ビットのディジタル出力を使って、0.3とか0.8とかいった中途半端なアナログ値を出力したいのです。どうすればよいでしょうか。
勘のするどい方はお気づきかもしれません。そうです、前回やった PWM です。
PWM によるアナログ値の出力
簡単のために1周期が8クロックの PWM を考えます。いま、オン幅を5クロックに設定しました。すると次のような波形が出力されるはずです。
1周期8クロックのうち、5クロックにわたって1が出力され、残りの3クロックが0になります。これが繰り返されますので、平均的に見ると、\(\frac{5}{8} = 0.625\) の値が出力されていると考えることができます。たとえば出力信号の電圧が 1 V なら、平均的には 0.625 V が出力されているとみなせるわけです。
もちろん、1周期があまりに長いと、ON と OFF を繰り返していることが分かってしまいますが、周期がそれなりに短ければ「アナログ的」な出力が可能になるわけです。
PDM によるアナログ値の出力
PWM と似ているものの、少し異なるアプローチもあります。PWM では1周期の中では「1」の区間と「0」の区間がそれぞれ1回ずつでしたが、もっと積極的に「1」と「0」をスイッチさせてもよいはずです。
たとえば、先ほどと同様に1周期を8クロックとして、次のような波形を考えます。
8クロック周期で「11011010」とういうパターンが繰り返されています。ラテン系のノリのリズムパターンですが、これは5個の「1」と3個の「0」から成り立っており、平均するとやはり0.625のアナログ値とみなせます。
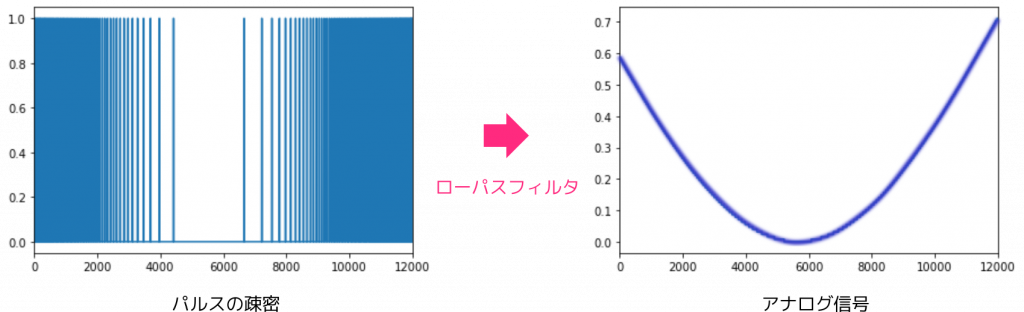
PWM と違って、「1」が出力される区間が全体的に分布していることが特徴です。その分、「1」と「0」のスイッチは頻繁に行われます。これはスイッチングが高い周波数で行われるということですので、ローパスフィルタに通すだけでスイッチングの影響を除去してアナログ信号を取り出せます。
この方式は PDM (Pulse Density Modulation: パルス密度変調) と呼ばれます。パルスの密度でアナログ値を表しているからです。この PDM の方式を用いたDA コンバータの代表選手がデルタシグマ型 DA コンバータです。
デルタシグマ型 DA コンバータの原理と構成
デルタシグマ型 DA コンバータは、ディジタル信号をデルタシグマ変調回路と呼ばれる回路で PDM 信号に変換し、それをローパスフィルタに通すことでアナログ信号に変換するコンバータです。通常、ローパスフィルタはアナログで作りますが、それ以外の部分はディジタル回路で構成できるため、FPGA 実装にも向いた方式です。
ディジタル信号の入力系列を \(x(n)\) で表すこととします。\(n \) はクロックサイクルの番号です。つまり、\(x(0)\) はクロック0における入力値、\(x(1)\) はクロック1における入力値といった具合です。\(x(n)\) は0以上1未満の数値を表すディジタルデータとします。
デルタシグマ変調回路は、この \(x(n)\) を PDM 信号の系列 \(y(n)\) に変換します。\(y(n)\) は0か1の値をとる2値信号の系列です。ここまでの処理を FPGA 上で行います。
なお「デルタシグマ」と呼ぶ流儀と「シグマデルタ」と呼ぶ流儀がありますが、どちらも同じことです。2種類の方法があるわけではありませんので、念のため。
それではデルタシグマ変調回路の構成と動作原理を見ていきましょう。
はじめにシグマがあった
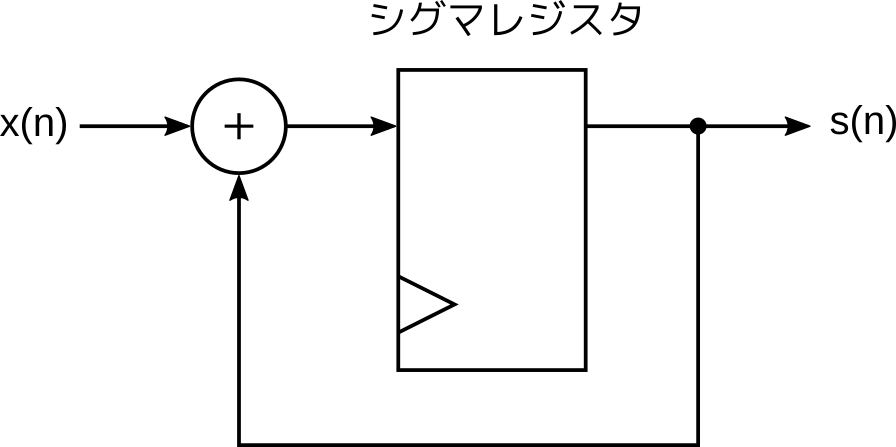
まあ、別にどこが最初でもいいのですが、RTL 設計では、やはりレジスタを中心にするのが考えやすいです。というわけで、デルタシグマ変調回路で使われる唯一のレジスタ (シグマレジスタと呼ぶことにします) の構造を見てみましょう。
レジスタの出力がフィードバックされて入力と加算されます。毎クロック、入力データがレジスタに加算されていきますので、レジスタの初期値を0とすれば、出力は \[
s(n) = \sum_{i = 0}^{n – 1} x(i)
\] と表されます。シグマと呼ばれる所以です。
さて、入力データをすべて加算して蓄積するというこの回路、しばしば積分回路とも呼ばれます。離散時間システムですので、本来は「和分」というべきですが、クロックの周期を0に近づけた極限をとれば積分になるからです。
わたしはデルタでありシグマである
積分回路があるなら微分回路もあります。本来は「差分」ですが、極限をとれば微分です。シグマに対してデルタです。次のような回路です。
\( x(n) \) が入力で \( d(n) \) が出力です。レジスタには入力信号の \(x(n)\) がそのまま入りますので、レジスタの出力は1クロック前の値である \(x(n-1)\) です。フィードバック経路には、符号反転の組み合わせ回路が入っています。符号反転の結果は \(-x(n-1) \) です。これが加算器に入ります。
したがって、微分回路の出力は \[
d(n) = x(n) – x(n-1)
\] と表せます。入力信号と1クロック前の入力信号の差分を出力するわけです。
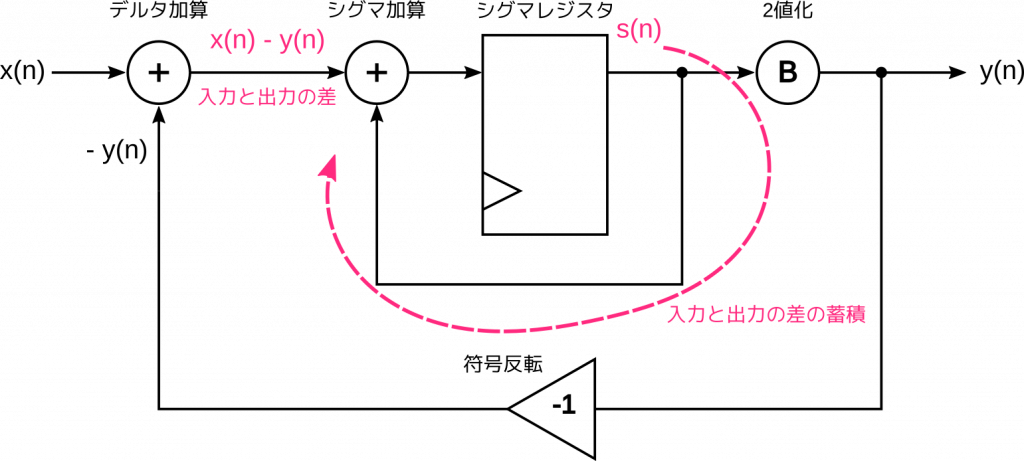
それでは、ここでデルタとシグマの回路をくっつけてみましょう。レジスタは1つに統合し、デルタの出力をループさせます。こんな感じです。
2つの加算器を区別するために、もともとシグマ回路にあったものをシグマ加算器、デルタ回路から来たものをデルタ加算器と呼ぶことにします。
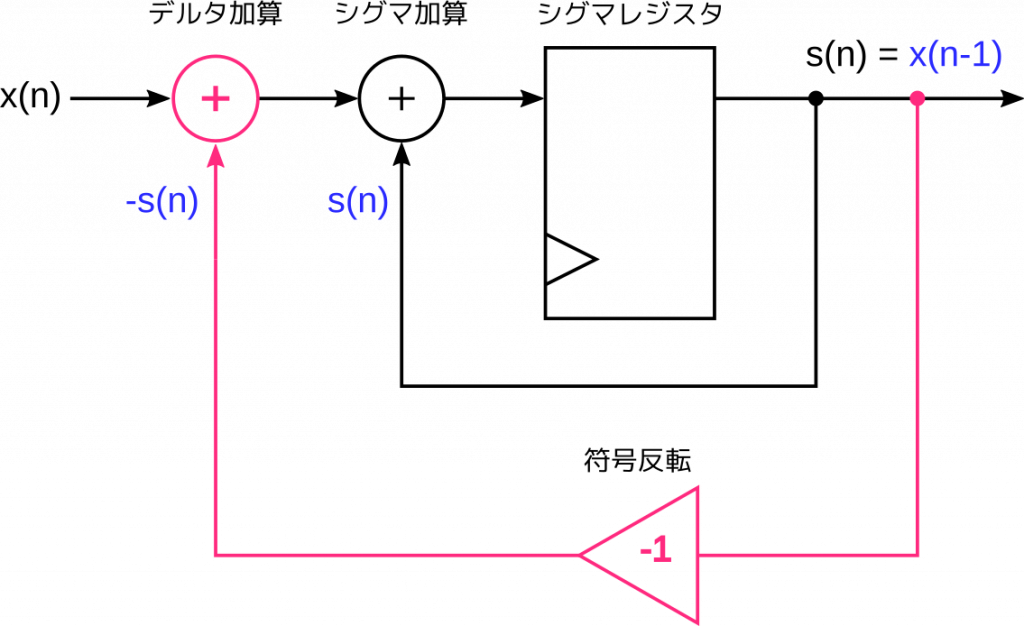
シグマレジスタの出力を \( s(n) \) とすると、デルタ加算の処理は \[ x(n) – s(n) \] と書けます。さらに、シグマ加算ではこのデルタ加算の結果に \( s(n) \) を加えます。
つまり、2つの加算器の動作は互いに打ち消し合います。結局、シグマレジスタには入力信号 \(x(n)\) そのものが入ります。レジスタの出力は、1クロック前の入力となりますので、\[
s(n) = x(n-1)
\] となります。ただのレジスタの動作と一緒になっちゃいましたね。積分したものを微分したら元に戻るということです。
0と1とを分けよ
ここに2値化を行う組み合わせ回路 (2値化器) を挿入します。
この2値化器はシグマレジスタの出力 \( s(n) \) を見て、必ず0か1のどちらかを出力します。どのような基準で0と1に分けるのかは、また後で詳しく考えます。2値化の結果が最終的な出力 \( y(n) \) です。
実はこれでデルタシグマ変調回路の完成です。シンプルですが、シンプルすぎていまいち動作原理が分かりにくいかもしれません。
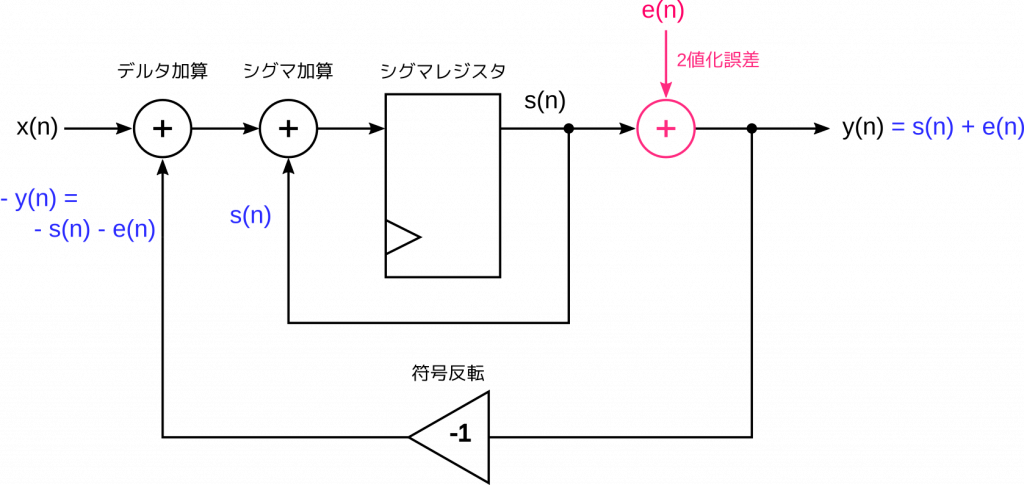
最後に加えた2値化器がポイントです。2値化器は \(s(n)\) を0か1かのどちらかに置き換えます。違う値に置き換えるわけですから、当然、誤差が発生します。2値化誤差です。見方を変えると、2値化とは \(s(n)\) に2値化誤差を加える処理と考えることもできます。図示するとこんな感じです。
\( e(n) \) が2値化誤差です。もちろん \( e(n) \) は正の値になったり負の値になったりします。
信号を追いかける
さて、順に信号を追っていきましょう。まず2値化のところから考えると、シグマレジスタの出力 \( s(n) \) に2値化誤差 \( e(n) \) を加えたものが出力 \( y(n) \) ですから、\[
y(n) = s(n) + e(n)
\] と書けます。
この \( y(n) \) は符号を反転されてデルタ加算器に入りますので、デルタ加算の計算は \[
\begin{align}
x(n) – y(n) &= x(n) – \left[s(n) + e(n) \right]\\
&= x(n) – s(n) – e(n)
\end{align}
\] と表せます。シグマ加算では、これにさらに \( s(n) \) を加えるので、シグマレジスタへの入力は、結局、 \[
\left[ x(n) -s(n) -e(n) \right] + s(n) = x(n) – e(n)
\] と表せます。ややこしくなってきましたが、この部分だけ図示すると次のようになります。
こう整理してみると、たいしたことないですね。
シグマレジスタへの入力が \( x(n) -e(n) \) になるところまで分かりました。この値は次のクロックの立ち上がりでレジスタに取り込まれますから、シグマレジスタの動作は \[
s(n+1) = x(n) -e(n)
\] という漸化式で表せます。1クロック前で考えれば \[
s(n) = x(n-1) – e(n-1)
\] です。
信号が一周してきて \( s(n) \) が求まりました。これをさきほどの2値化処理の式に入れてみます。すると、出力 \( y(n) \) は、\[
\begin{align}
y(n) & = s(n) + e(n) \\
& = \left[ x(n-1) – e(n-1) \right] + e(n)\\
& = x(n-1) + \left[ e(n) – e(n-1)\right]
\end{align}
\] と表すことができます。出力の部分だけ図示するとこのような感じです。
出力 \( y(n) \) を入力と2値化誤差を使って表すことができました。
動作式を解釈する
それでは、導出されたデルタシグマ変調回路の動作の式 \[
y(n) = x(n-1) + \left[ e(n) – e(n-1) \right]
\] を解釈してみましょう。
入力信号はそのまま出力
まず、右辺の1つ目の項の \( x(n-1) \) は、1クロック前の入力信号を意味しています。レジスタが入っていますので、入力が1クロック遅れて出力に現れるのは、ある意味当たり前です。むしろ、入力信号が変形されずにそのまま出力されるという点が重要です。
2値化誤差は微分して出力
次に、右辺2つ目の項の \( \left[ e(n) – e(n-1) \right] \) は、今発生した2値化誤差 \(e(n)\) と1クロック前に発生した2値化誤差 \( e(n-1) \) の差の形になっています。つまり、この1クロックで2値化誤差がどれだけ増加したかを示しています。これは2値化誤差の差分、極限をとれば微分です。
つまり、デルタシグマ変調の出力は、「1クロック前の入力信号」+「2値化誤差の微分」なのです。
ノイズシェーピング
2値化誤差の「微分」というところがミソです。微分は低周波成分を抑制し、高周波成分を強調するハイパスフィルタの機能をもつからです。
たとえば、周波数 \(f\) の正弦波は時刻を \(t \) として、 \[
w(t) = \sin( 2 \pi f t)
\] と書けますが、この微分をとると、\[
\frac{dw(t)}{dt} = 2 \pi f \cos (2 \pi f t)
\] となります。微分後の波の振幅に係数 \(2 \pi f \) がつくことから、低周波成分は抑制され、高周波成分ほど強調されることが分かります。
一般に、2値化の誤差はランダムに発生し、その成分は低周波域から高周波域まで一様に分布します。ホワイトノイズです。これを微分することによって、ノイズの分布をわざと高周波側に偏らせているのです。
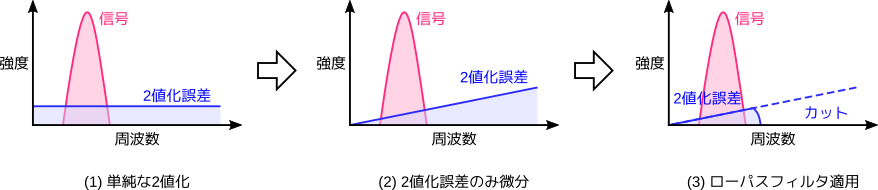
高周波域に移動したノイズはどうなるのでしょうか? 心配ありません。PDM 信号は最後にローパスフィルタを通してアナログ化されるのを思い出してください。このローパスフィルタによって高周波域のノイズはまとめてカットされるのです。
ちょうど2値化誤差のノイズの分布を周波数軸上で整形するようなイメージから、この手法はノイズシェーピングと呼ばれます。2値化誤差をそのまま出力するのに比べて、信号帯域のノイズが減少するのがお分かりいただけると思います。
2値化の手法
先ほど保留していた2値化の具体的な手法について考えます。やりたいことは、シグマレジスタの出力 \( s(n) \) を見て、\( y(n) \) を0か1に決めることです。なるべくなら誤差が少ない方が嬉しいです。
ここでデルタシグマの動作を少し違った角度から見てみます。デルタ加算器では、入力 \( x(n) \) と出力 \( y(n) \) の差 \( x(n) – y(n) \) をとっています。そして、その入力と出力の差がシグマレジスタに蓄積 (積分) されていきます。それが \( s(n) \) です。
このように考えると、シグマレジスタの値は、\[
\begin{align}
s(n) & = \sum_{i=0}^{n-1} \left( x(i) – y(i) \right) \\
& = \sum_{i=0}^{n-1} x(i) – \sum_{i=0}^{n-1} y(i)
\end{align}
\] と表すこともできるはずです。
このように、デルタシグマ変調回路は、\(x(n)\) を目標値として \(y(n)\) を制御するフィードバックシステムとしてとらえることもできるのです。この観点から、\( y(n) \) をどう2値化すべきか、\( s(n) \) の値を場合分けして考えてみます。
\( s(n) > 0\) のとき
\( s(n) > 0\) ということは、\[
\sum_{i=0}^{n-1} x(i) > \sum_{i=0}^{n-1} y(i)
\] ということですから、これまでのトータルでは、入力値に比べて出力値が不足気味です。ここはひとつ、パルスをオンにして出力値を上昇させてやるべきでしょう。つまり、\( y(n) = 1 \) です。
\( s(n) < 0 \) のとき
大小関係が反対ですから、これまでのところ入力値に比べて出力値が過剰気味です。よって、\( y(n) = 0 \) として出力値を減少させるべきでしょう。
\( s(n) = 0 \) のとき
どちらでも大差なさそうです。なんとなく、\( y(n) = 0 \) とする方が自然な気もしますが、正負の判定を \( s(n) \) の MSB (Most Significant Bit: 最上位ビット) で行うなら、0は正の数の仲間に入れて \( y(n) = 1 \) とした方が回路が簡単になります。
以上をまとめると、\[
y(n) =
\begin{cases}
1 & (s(n) \ge 0) \\
0 & (s(n) < 0)
\end{cases}
\]
と2値化すればよいことが分かります。
設計と実装
これでデルタシグマ変調回路の原理は理解できました。さっそく FPGA で作ってみましょう。
ビット幅の検討
設計の際には演算器やレジスタのビット幅を明確にしておく必要があります。まず、ディジタル値入力のビット幅を \( N \) ビットとし、これは パラメータとして与えることにします。
小数の世界から整数の世界へ
ここまで、ディジタル値の入力 \( x(n) \) は0以上1未満の値と考えてきました。もちろん、このまま固定小数点数と考えて設計を進めてもよいのですが、やはり整数の方が考えやすいです。\( 2^{N} \) 倍して考えましょう。また、具体的な数値をイメージした方が考えやすいので、ここではとりあえず \( N= 8 \) とします。
すると、入力のディジタル値 \( x(n) \) は8ビットです。これを符号なし数と考えると、0から255までの数を表現できます。パルス出力はハードウェアとしては当然1ビットです。ただ、小数を整数化するため \( 2^{N} \) 倍して考えていますので、パルス出力が「1」のとき、\( y(n) \) の内部的な数値としての意味は256になります。
では、シグマレジスタの値 \( s(n) \) がとり得る範囲について考えます。シグマレジスタの動作式は、\[ s(n+1) = s(n) + x(n) – y(n)\] でした。最大値や最小値がどうなるのか、\( s(n) \) が0以上のときと0未満のときに分けて考えてみます。
\( s(n) \ge 0 \) のとき
2値化の手法のところで説明したように、このときのパルス出力は「1」です。つまり、 \( y(n) = 256 \) ですので、シグマレジスタの動作は\[
s(n+1) = s(n) + x(n) – 256
\] と書けます。
\(0 \le x(n) \le 255\) かつ \( s(n) \ge 0 \) であることを考えると、\(s(n+1)\) の最大値と最小値は、それぞれ\[
s(n+1) =
\begin{cases}
s(n) – 1 & (\text{max}) \\
-256 & (\text{min})
\end{cases}
\]となります。つまり次のことが分かります。
- シグマレジスタの値が0以上のときは、次のクロックでは減ることはあっても増えることはない
- 減ったとしても-256よりも小さくなることはない
\( s(n) < 0 \) のとき
このときのパルス出力は「0」です。つまり \( y(n) = 0 \) です。よって、シグマレジスタの動作は\[
s(n+1) = s(n) + x(n)
\] と書けます。
\(0 \le x(n) \le 255 \) かつ \( s(n) < 0 \) であることを考えると、\( s(n+1) \) の最大値と最小値は、それぞれ\[
s(n+1) =
\begin{cases}
254 & (\text{max}) \\
s(n) & (\text{min})
\end{cases}
\] となります。つまり次のことが分かります。
- シグマレジスタの値が負のときは、次のクロックでは増えることはあっても減ることはない
- 増えたとしても254よりも大きくなることはない
結論
ということで、シグマレジスタの値がとる範囲は-256から254であることが分かりました。2の補数で-256を表現するには9ビット必要ですので、シグマレジスタのビット幅は9ビットとなります。
一般化すると、ディジタル値の入力が \( N \) ビットならば、シグマレジスタは \( (N+1) \) ビット必要です。また、後でもう一度確認しますが、加算処理についても \( (N+1) \) ビットで大丈夫です。
注意が必要なのは、入力可能なディジタル値は最大で \( 2^N – 1 \) という点です。8ビットなら255であり、256ではありません。このため出力を 100 % の区間で「1」にすることはできません。これは前回の PWM 回路と同様です。もし、完全な直流の「1」も出力したい場合は、ビット幅の設計を見直す必要があります。
デルタシグマ変調回路の記述例
ビット幅も決まりましたので、SystemVerilog で記述してみましょう。他のデザインでも再利用できるように、独立したモジュールとします。入出力は3ポートだけです。
- クロック入力: clk
- ディジタル値入力: data_in
- パルス出力: pulse_out
data_in のビット幅はパラメータ WIDTH で指定するようにしました。
`default_nettype none
module delta_sigma
#(
parameter int WIDTH = 16
)
(
input wire clk,
input wire [WIDTH-1:0] data_in,
output logic pulse_out
);
logic [(WIDTH+1)-1:0] sigma_reg = '1; // シグマレジスタ
always @(posedge clk) begin
sigma_reg <= sigma_reg + {pulse_out, data_in}; // デルタ加算とシグマ加算
end
assign pulse_out = ~sigma_reg[(WIDTH+1)-1]; // 2値化
endmodule
`default_nettype wireモジュール化することで、かえって記述量が増えてしまうくらい単純です。何点か補足しましょう。
2値化器の記述
2値化処理は19行目です。シグマレジスタ (sigma_reg) が0以上なら pulse_out を1に、負なら0にします。2の補数表現では MSB が1なら負の値ですから、シグマレジスタの MSB を反転して pulse_out に接続すれば OK です。シグマレジスタのビット幅は (WIDTH + 1) であることに注意しましょう。
前回説明したように、組み合わせ回路の出力をそのまま外部に出す際にはグリッチに注意が必要です。しかし、この2値化器はシグマレジスタの MSB を反転するだけですので、1入力の組み合わせ回路 (1入力NOT) です。1入力ならグリッチの心配はありません。というわけで、そのまま出力させています。
シグマレジスタの記述
シグマレジスタの動作は、 \[
s(n+1) = s(n) + x(n) – y(n)
\]と書けるのでした。また、小数の世界から整数の世界へ移行したことで、\(y(n)\) の内部的な数値としての意味は \[
y(n) =
\begin{cases}
0 & (\text{pulse_out}=0) \\
2^N & (\text{pulse_out}=1)
\end{cases}
\]と \( 2^N \) 倍になるのでした。ここで pulse_out は1ビットのパルスの出力です。代入すると、シグマレジスタの動作は、\[
s(n+1) =
\begin{cases}
s(n) + x(n) & (\text{pulse_out} = 0)\\
s(n) + x(n) – 2^N & (\text{pulse_out} = 1)
\end{cases}
\]と書けることになります。
さて、シグマレジスタのビット幅は \((N+1)\) ビットです。\((N+1)\) ビットの2の補数表現で \(-2^N\) を表すと、MSB だけ1になり、あとのビットはすべて0です。ということは、\((N+1)\) ビットの2の補数の世界では、\( – 2^N \) のことを左シフト演算を使って \[
1 \ll N
\] と表すことができます。
これを使うと、さきほどのシグマレジスタの動作は、\[
s(n+1) =
\begin{cases}
s(n) + x(n) & (\text{pulse_out} = 0)\\
s(n) + x(n) + (1 \ll N) & (\text{pulse_out} = 1)
\end{cases}
\]と書けます。ちなみに、\(( 1 \ll N )\) 自体が負の数を表すので、減算が加算に変わりました。
さて、2つの式をまとめて、\[
s(n + 1) = s(n) + x(n) + (\text{pulse_out} \ll N)
\]と書くこともできます。0はいくらシフトしても0のままだからですね。
ここで、シグマレジスタ \( s(n) \) のビット幅は \((N+1)\) ビットなのに対し、入力値 \( x(n) \) は \(N\) ビットの符号なし数だったことを思い出してください。すると \( N \) ビット左シフトして \( x(n) \) に足すという処理は、連接を使うと、\[
s(n + 1) = s(n) + \{\text{pulse_out}, x(n)\}
\]と表せます。これが16行目の記述です。ちょっとトリッキーですが、シグマ加算とデルタ加算をまとめて \(( N+1 )\) ビットの加算器で実現できることが納得できます。
シグマレジスタの初期値
ところで今回の2値化の処理では、シグマレジスタが0の場合は、正の値と判断してパルス出力を1にするように設計しました。このお陰で、2値化の処理はシグマレジスタの MSB を反転するだけで済んだのですが、シグマレジスタの初期値を0とすると、入力値に関わらず起動時には必ずパルス出力が1になります。もちろん、入力値が小さければ、このパルスはすぐに0になるのですが、ちょっと気持ち悪いです。
というわけで、13行目ではシグマレジスタの初期値を-1 (全ビット1) にしています。
いや、こっちの方がよっぽど気持ち悪いという方は、2値化の際に0は負と判断すればすっきりします。ただ、2値化器が1入力の組み合わせ回路ではなくなりますので、グリッチ対策のフリップフロップが別途必要になります。
FPGA ピアノに統合
さあ、いよいよピアノと合体です。前回の設計をベースに、パルス波の振幅をスライドスイッチで設定できるようにします。PDM のビット幅は16ビットとします。入出力インタフェースは変更ありません。全体の構成図は次のとおりです。
PWM 波を生成する所までの仕組みは前回と同じですが、Arty はスライドスイッチが4つだけなので、今回はデューティ比は固定としました。また、今回の PWM 波は2値ではなく振幅をもつため、16ビットのレジスタ data_for_pdm に格納するようにしています。これがデルタシグマ変調回路へ入力されます。
`default_nettype none
module pdm_sound
#(
parameter real CLK_FREQ = 100e6, // クロック周波数 (Hz)
parameter int COUNT_WIDTH = 32, // カウンタビット幅
parameter int PDM_WIDTH = 16 // PDM ビット幅
)
(
input wire clk,
input wire [3:0] btn_in, // ボタン入力
input wire [3:0] sw_in, // スライドスイッチ入力
output logic led_out,
output logic pulse_out
);
localparam real BASE_FREQ = 442.0; // 基準音の周波数
localparam bit [COUNT_WIDTH-1:0] INCS[4] = '{ // カウンタの増分値
n2inc(-4), n2inc(-5), n2inc(-7), n2inc(-9) // ファ,ミ,レ,ド
};
localparam [COUNT_WIDTH-1:0] DUTY = 1'b1 << (COUNT_WIDTH-1); // デューティ50%
logic [COUNT_WIDTH-1:0] count = '0; // カウンタ
logic [PDM_WIDTH-1:0] data_for_pdm = '0; // デルタシグマ変調の入力データ
always @(posedge clk) begin
if (btn_in == '0)
count <= '0; // どのボタンも押されていなければカウンタをクリア
else begin
for (int i = 0; i < 4; i++) begin
if (btn_in[i]) begin
count <= count + INCS[i]; // 押されたボタンに対応する増分値を加える
break;
end
end
end
end
always @(posedge clk) begin
if (btn_in != '0 && count < DUTY) // PWM 発生用の比較器
data_for_pdm[(PDM_WIDTH-1)-:4] <= sw_in;
else
data_for_pdm <= '0;
end
// デルタシグマ変調
delta_sigma
#(
.WIDTH(PDM_WIDTH)
)
delta_sigma_inst
(
.clk(clk),
.data_in(data_for_pdm),
.pulse_out(pulse_out)
);
assign led_out = pulse_out; // 確認用 LED 出力
// 基準音の距離からカウンタの増分値を計算する関数
function bit [COUNT_WIDTH-1:0] n2inc(int n);
return ((2.0 ** (COUNT_WIDTH + n / 12.0)) * BASE_FREQ / CLK_FREQ);
endfunction
endmodule
`default_nettype wire前回のソースコードからの変更点はわずかです。26行目から37行目のカウンタの記述はまったく同じです。21行目ではデューティ比をパラメータとして設定しています。この例では MSB だけ1にして、50 % に設定しています。
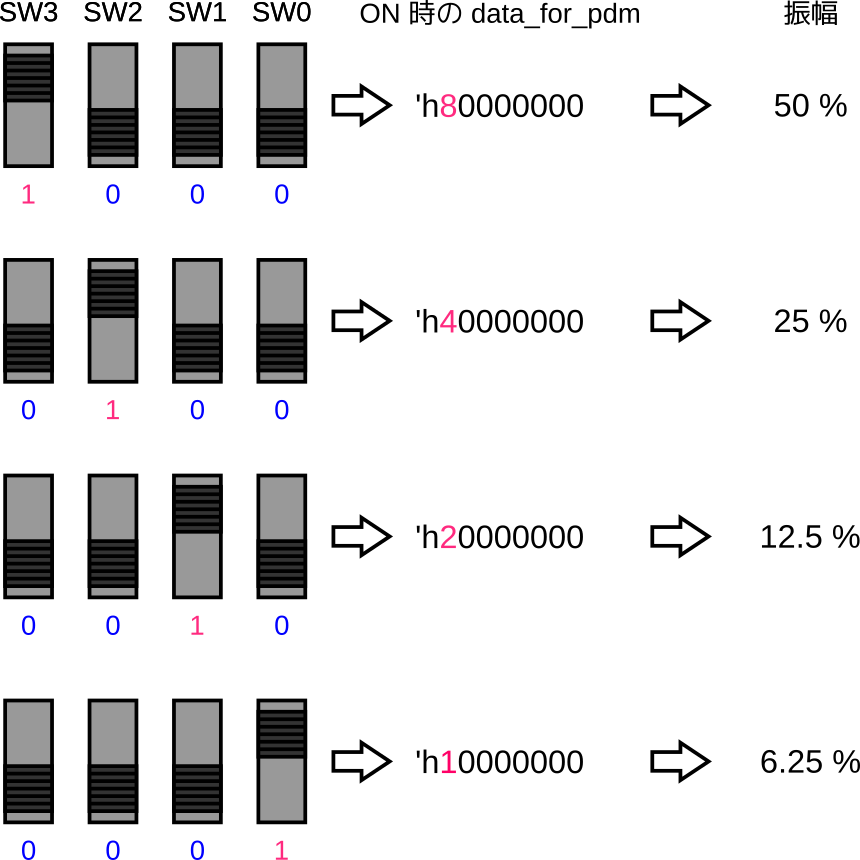
39行目から44行目の PWM 波生成の仕組みも前回と同じですが、振幅をもたせるために、PWM が ON のときにはスライドスイッチの入力が data_for_pdm レジスタの上位4ビットに入るようになっている点が異なります。この振幅の設定の仕方は、前回のデューティ比の設定と一緒です。
47行目から56行目でデルタシグマ変調回路を実体化しています。これで音量を変えながら音階を鳴らすことができるはずです。
なんちゃってディジタル・アナログ協調シミュレーション
では、シミュレーションで動作を確かめてみましょう。といっても、生の PDM の出力波形を見てもいまいちピンときません。ローパスフィルタを通した後のアナログ信号の波形を確認したいです。このためには、RTL 記述のディジタルシミュレーションと、ローパスフィルタのアナログシミュレーションを連携させる必要があります。
Verilog-AMS などのミックスドシグナル検証用の環境もありますが、今回は高精度なアナログシミュレーションは必要なく、ローパスフィルタをかけた結果をちょっと確認したいだけです。このような用途では SystemVerilog だけでも十分に対応可能です。
ローパスフィルタの数値モデリング
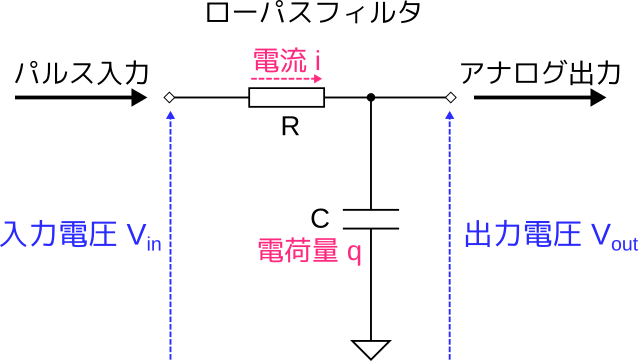
ローパスフィルタは前回作成したアンプ回路に付けていましたね。抵抗とコンデンサによる簡単なものです。
この回路の振る舞いを数値計算するために数式でモデリングします。
まず、コンデンサの電荷と電圧の公式を思い出しましょう。コンデンサに蓄えられた電荷を \( q\) とすれば、この回路では極板間の電圧は \( V_\mathrm{out} \) ですから、\( q = C V_\mathrm{out} \) です。
また、抵抗を流れる電流を \(i\) とすれば、オームの法則より、\[
Ri + V_\mathrm{out} = V_\mathrm{in}
\] です。これは \( q = C V_\mathrm{out} \) を使うと、\[
Ri + \frac{q}{C} = V_\mathrm{in}
\] と書けます。
電流は単位時間に移動する電荷量のことです。この回路では移動した電荷はすべてコンデンサに蓄えられますから、蓄えられた電荷量の微分が電流 \(i\) です。つまり、 \[
i = \frac{dq}{dt}
\] と書けます。ひとつ前の式に代入すると、\[
R \cdot \frac{dq}{dt} + \frac{q}{C} = V_\mathrm{in}
\] という \( q\) に関する微分方程式が得られます。
ただ、今回はコンデンサの電荷量にはあまり興味はありません。そこで、再び \( q = C V_\mathrm{out} \) を代入すると、\[
RC \cdot \frac{d V_\mathrm{out}}{dt} + V_\mathrm{out} = V_\mathrm{in}
\] という微分方程式が得られます。これを解けばよさそうです。
オイラー法
解くといっても、SystemVerilog のシミュレータに数値計算してもらうのです。そのためには数値積分のアルゴリズムが必要です。今回は精度を求めているわけではないので、シンプルなオイラー法を使うことにします。
さきほどの微分方程式を、\( V_\mathrm{in} \) と \( V_\mathrm{out} \) が時間の関数であることを強調して記述すると、\[
RC \cdot \frac{d V_\mathrm{out}(t)}{dt} + V_\mathrm{out}(t)
= V_\mathrm{in}(t)
\] となります。ここで、微分を\[
RC \cdot \frac{V_\mathrm{out}(t ) – V_\mathrm{out}(t – \Delta t)}{\Delta t} + V_\mathrm{out}(t)
= V_\mathrm{in}(t)
\] のように微小時間 \( \Delta t \) を使って近似します。これは1次後退差分という近似です。
あとは機械的に式変形します。両辺を \( \Delta t \) 倍すると、\[
RC \cdot V_\mathrm{out}(t) – RC \cdot V_\mathrm{out}(t – \Delta t) + \Delta t \cdot V_\mathrm{out}(t)
= \Delta t \cdot V_\mathrm{in}(t)
\] となり、\(V_\mathrm{out} (t – \Delta t)\) の項を移項して整理すると、\[
(RC + \Delta t) V_\mathrm{out}(t) = RC \cdot V_\mathrm{out}(t – \Delta t) + \Delta t \cdot V_\mathrm{in}(t)
\] となり、さらに両辺を \( (RC + \Delta t) \) で割って、\[
V_\mathrm{out}(t) = \frac{RC \cdot V_\mathrm{out}(t – \Delta t) + \Delta t \cdot V_\mathrm{in}(t)}{RC + \Delta t}
\] を得ます。
これは時刻 \( t \) における入力電圧 \(V_\mathrm{in}(t)\) とひとつ前の時刻の出力電圧 \(V_\mathrm{out}(t – \Delta t)\) から、今の出力電圧 \(V_\mathrm{out}(t)\) を計算する漸化式です。\( V_\mathrm{in}(t) \) は PDM 波形の電圧ですから、 RTL シミュレーションで求まります。よって初期値さえ与えれば、この漸化式を \( \Delta t \) ごとにひたすら計算することで \( V_\mathrm{out}(t) \) の波形が求まるのです。これなら SystemVerilog でも書けます。
SystemVerilog による数値計算
シミュレーションモジュールの記述例を抜粋で示します。ファイル全体は Gist からダウンロード可能です。
`timescale 1ns/1ps
...
localparam real R = 22.2e3; // 22.2kohm
localparam real C = 100.0e-12; // 100 pf
localparam real DELTA_T_NS = 1.0;
localparam real DELTA_T = DELTA_T_NS * 1.0e-9;
real v_in, v_out = 0.0;
always #DELTA_T_NS begin
v_in = pulse_out? 3.3: 0.0;
v_out = (R * C * v_out + DELTA_T * v_in) / (R * C + DELTA_T);
endこの例では \(\Delta t\) を 1 ns としており、always # ブロックを使って、1 ns ごとに漸化式を反復計算しています。timescale を1 ns としているので、#1 が 1 ns を表しますが、漸化式では 1.0e-9 として数値計算する必要があります。エレガントではありませんが、DELTA_T_NS と DELTA_T の2つのパラメータを使っているのはそのためです。
v_in は RTL モジュールの出力である pulse_out 信号によって、3.3 V か 0 V が選択されるようになっています。v_out は初期値は 0 V にしています。漸化式の部分は v_out の変数が上書き更新される点を除けば、先ほど導出した式そのままです。
シミュレーション結果
それではシミュレーション結果を見てみましょう。
スライドスイッチ (sw_in) により、振幅を50 %、25 %、12.5 % と変化させていますが、それに応じて v_out の振幅がちゃんと変化していることが確認できます。pulse_out が分かりにくいので拡大してみます。
pulse_out の PDM 波形が確認できました。このレンジで見ると v_out の立ち上がりが鈍っていることも分かり、確かにローパスフィルタとして機能していることが確認できます。
実機動作確認
前回の実装とまったく同じハードウェアセットアップで実機動作を確認してみました。トップモジュールもモジュール名以外は同じです。Arty A7-35T 用の IO ピン割り当てファイルを含むソースコードは Gist からダウンロードできます。以下ではパルスの振幅は 50%、25%、12.5%、6.25% の4パターンとして音階の鳴動を確認しています。
音色は変化せずに音量だけが変化するのが確認できたと思います。また、設定した振幅に応じて、確認用 LED の明るさが変化するのも確認できたと思います。LED にはデルタシグマの出力がローパスフィルタを通さずに直接繋がっていますが、いわばわれわれの目がローパスフィルタとして働いているのです。
まとめ
- デルタシグマ変調した PDM 波形をローパスフィルタに通せばアナログ信号が得られる
- 積分とは入力信号をひたすら足していくことである
- 微分とは入力信号と1クロック前の入力信号の差をとることである
- デルタシグマ変調回路は微分と積分と2値化でできている
- 入力信号は微分と積分で元に戻りそのまま出力される
- 2値化誤差は微分されて出力される (ノイズシェーピング)
- 一種のフィードバック制御システムとしても解釈できる
- SystemVerilog に数値計算させれば簡単なディジタル・アナログ協調シミュレーションも可能
さて、せっかくデルタシグマ型 DA コンバータが完成したのに、パルス音の振幅を数段階変えるだけなんてつまらないですね。そもそも、これでは本当に DA コンバータとして動いているのか、いまいち確信がもてません。次回は FPGA で正弦波を生成し出力させてみます。
長崎大学・柴田 裕一郎