この連載では、少しホビーエレクトロニクス的なテイストも交えながら、FPGA ボードのスイッチボタンを鍵盤に見立てた電子ピアノの作成例をご紹介します。
オーディオ信号の出力となると、FPGA に DA コンバータを接続し、ディジタル信号をアナログ信号に変換するというのが普通かと思います。実際、廉価な FPGA ボードでもオーディオ用 DA コンバータを備えているものがかなりありますし、DA コンバータを搭載した拡張基板も色々とあるのですが、本連載ではあえて「DA コンバータがなくてもできる」をコンセプトとします。もちろん FPGA に DA コンバータを繋ぐのが悪いわけではありません。単になるべく多くの方にお手元の FPGA ボードで試していただけるように、というのがそのココロです。それでも、デルタシグマ変調で正弦波の和音を出力したりと、それなりに面白いことができます。
説明には Digilent の Arty A7-35T を使いますが、入力ボタンがいくつかあり、1ビットのディジタル信号が出力できれば、他の FPGA ボードでも OK です。どんな回路でも正しく動作したときは嬉しいものですが、設計した回路から音が出るというのもまた楽しいものです。それではさっそく始めましょう。
パルス波の生成
ご存知のように音は空気の振動です。まずは FPGA で振動する電気信号を作り出す必要があります。今回は FPGA から出力するのは1ビットだけですので、値は0か1の2つです。これで作り出すことのできるもっとも簡単な振動は、0と1を一定のリズムで交互に繰り返すパルス波でしょう。
原理は L チカと同じ
そうです。皆さんも一度はカウンタの出力を LED に接続して点滅させる回路 (いわゆる「L チカ」) を試したことがあると思いますが、同じことをすればよいのです。例えば32ビットのカウンタを用意し、その MSB (最上位ビット) を LED に 出力することを考えます。SystemVerilog で書くとこんな感じです。
`default_nettype none
module count32
(
input wire clk,
output logic led_out
);
// カウンタ用の32ビットレジスタ
logic [31:0] count = '0;
// 毎クロック 1 を加える
always @(posedge clk) begin
count <= count + 32'd1;
end
// カウンタの MSB を出力
assign led_out = count[31];
endmodule
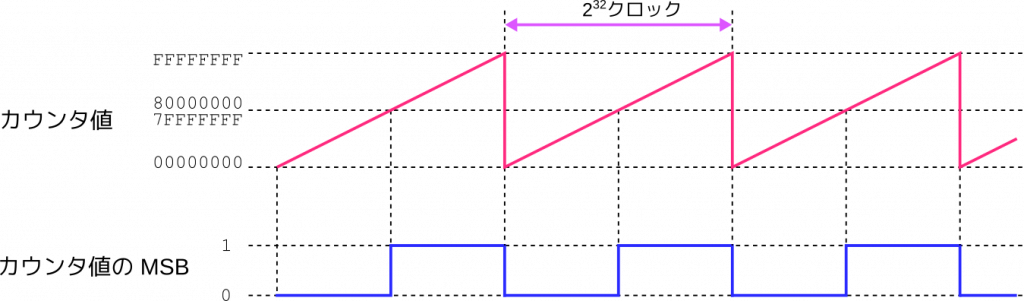
`default_nettype wireclk の周波数が100 MHz だとすると、LED は何秒間隔で点滅するでしょうか? 1クロックの周期は100 MHz の逆数で10 ns、32ビット のカウンタが一周するのに232クロックかかりますから、周期は $$\frac{2^{32}}{100\,\text{MHz}} \approx 43\,\text{s}$$ となります。このうち、カウンタの MSB の値は周期の前半が0、後半が1になりますので、43秒の半分の21.5秒間隔でついたり消えたりを繰り返すことになります。これを図にすれば、
というパルス状の波になります。周期と周波数は逆数の関係ですので、このパルス波の周波数は、$$\frac{100\,\text{MHz}}{2^{32}} = 0.0233\,\text{Hz}$$ ということになります。
狙った周波数を生成する
それではここで、ちょっとカウンタのソースコードを変更して、1クロックに2ずつ足すようにしてみましょう。先程のコードの11行目から13行目の部分を次のようにするだけです。
always @(posedge clk) begin
count <= count + 32'd2;
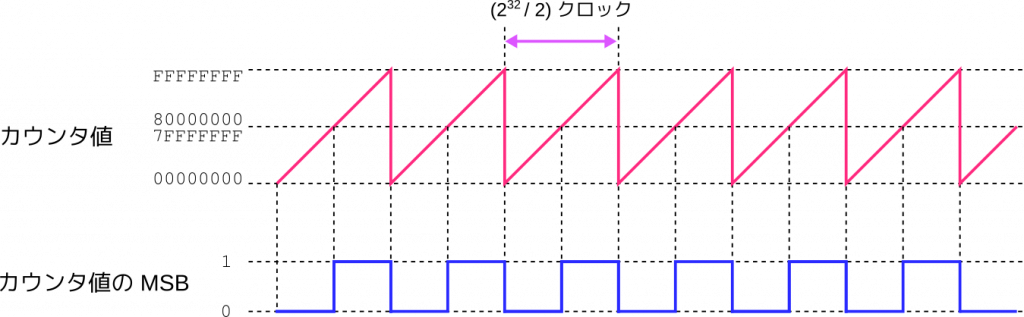
endすると LED の点滅の間隔はどうなるでしょうか? カウンタ値の増分値が2になるということは、ちょうど階段を2段ずつ登っていくようなイメージになります。すると次の図に示すように、LED の点滅の間隔は先ほどの半分になり、パルス波の周波数は倍の0.0466 Hz となります。同様に、1クロックあたりのカウンタの増分値を3にすると、パルス波の周波数は元の3倍の0.0698 Hz となります。
ということは、カウンタの増分値を設定することで狙った周波数のパルス波を生成できるのです。 いま、目的のパルス周波数を \(f_p\)、クロックの周波数を \(f_c\) とし、カウンタのビット幅を \(w\)、カウンタの1クロックあたり増分値を \(i\) すると、$$ f_p = \frac{f_c}{2^{w}} i$$ となります。これを \(i\) について解くと、$$ i = \frac{2^{w}}{f_c} f_p $$ となり、目標とするパルス波の周波数 \(f_p\) からカウンタの増分値 \(i\) を計算できるようになります。ここで、\( \frac{f_c}{2^{w}}\) の値は、実現可能なパルス周波数の分解能になります。同じクロック周波数でも、\(w\) を大きくとることで、より細かくパルス周波数を調整できることが分かります。
パルス音発生システム
全体の構成
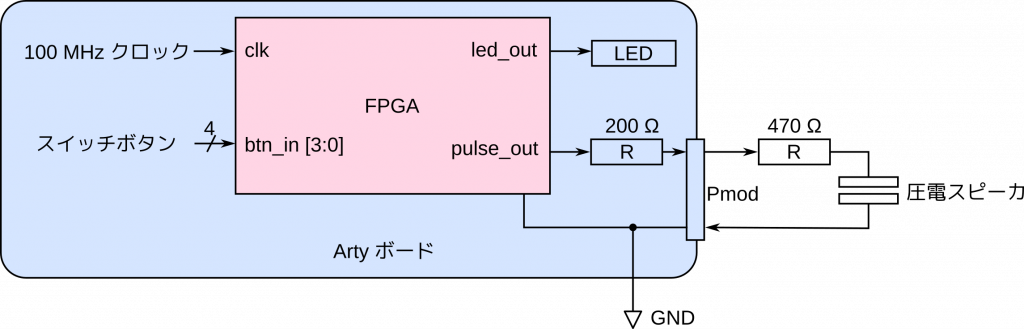
パルス波の生成方法も分かりましたので、電子ブザー的なものなら作れるような気がしてきました。さっそく設計にとりかかりましょう。やはりボタンを押したら音が鳴るというのが定番でしょう。Arty にはボタンが4個並んでいますので、それぞれに異なる周波数を割り当て、4種類のパルス音を比較できるようにしてみましょう。肝心の音を鳴らす部分は、さすがに FPGA でというわけにはいかないので、圧電スピーカ (圧電サウンダ) を Pmod コネクタを介して接続することにします。また、確認のために、パルス波の出力を LED にも接続するようにします。こうすることで、音が鳴らなかったときに、発音のメカニズムに問題があるのか、パルス波の出力そのものに問題があるのかを切り分けることができるようになります。全体の構成を図示すると次のようになります。
パルス波の周波数は、なんでも良いのですが、人間の可聴周波数はおおむね20 Hzから20 KHz といわれています。圧電スピーカは数 KHz 程度の音がもっともよく鳴るように作られたものが多いですので、とりあえず、500 Hz、1 KHz、2 KHz、4 KHz としておきましょう。
発音素子と駆動電流
身の回りの発音素子には、PC に接続するスピーカやヘッドフォンもありますが、これらはインピーダンスが低く FPGA に直接繋ぐのは無理があります。インピーダンスというのは、大雑把にいえば交流に対する抵抗成分です。インピーダンスが低いということはそれだけたくさん電流を流す必要があるということです。しかし FPGA の IO ピンが駆動できる電流には限界があります。例えば Artix-7 のデータシートによれば、 IOSTANDARD が LVCMOS33 に設定されたピン (Pmodのピン) が駆動可能な電流は最大で 16 mA です。
ここに最大出力 0.2 W、インピーダンスが 8 Ω の小型スピーカがあるとします。細かいことを置いておいてざくっと考えます。電力 \(W\) は電圧 \(V\)と電流 \(I\) の積ですから、オームの法則 \(V = IR\) を用いると
$$ W = IV = I^2R $$
と表せます。したがって、\( I = \sqrt{\frac{W}{R}} \) となります。\(W \) と \(R\) にそれぞれ 0.2 W、8 Ω を代入すると、\(I\) は158 mAとなり、これを無理矢理流せば FPGA が壊れてしまいます。仮に出力を 10 mW としても、電流は 35 mA となります。というわけで、スピーカやヘッドフォンを FPGA から直接駆動することは難しいのです。
一方、電子工作の分野ではお馴染みの圧電スピーカはインピーダンスがとても高く、鳴らすのにほとんど電流を必要としません。あまり大きな音を出すことは得意ではなく、周波数によっても音量が大きく変わってしまうのですが、目覚まし時計、体温計、メロディつきギフトカードなどにも使われています。最初の実験には最適です。筆者は手元にあった村田製作所の PKM17EPP-4001-B0 を使いましたが、もちろんどのようなものでも構いません。
圧電スピーカの繋ぎ方
さて、圧電スピーカの FPGA への繋ぎ方ですが、村田製作所の圧電サウンダ、圧電振動板 (他励振タイプ) の駆動回路例を教えてくださいのページにあるように、FPGA の IO と GND 間に直結するのではなく、直列に 470 Ω から 1 KΩ 程度の抵抗を挿入することが推奨されています。この抵抗がなくても音が鳴らないわけではありませんが、「安定鳴動および IC 保護のため」とありますので入れたほうが良いでしょう。
Arty のリファレンスマニュアルによれば、Pmod JA のコネクタと FPGA の間には保護用に 200 Ω の抵抗が入っていますので、これと合わせて圧電スピーカへ直列に 470 Ω から 1 KΩ の抵抗が入るように外付けの抵抗を選べば OK です。筆者は外付け抵抗を470 Ω としました。IOSTANDARD は LVCMOS33 として、3.3 V のパルス波を出力します。データシートによれば PKM17EPP-4001-B0 は 10 V くらいかけても大丈夫なので電圧そのものは心配ありません。ただし、直流を長時間かけないようにとの注意書きがあります。パルス出力を1に固定しないように十分注意する必要があります。
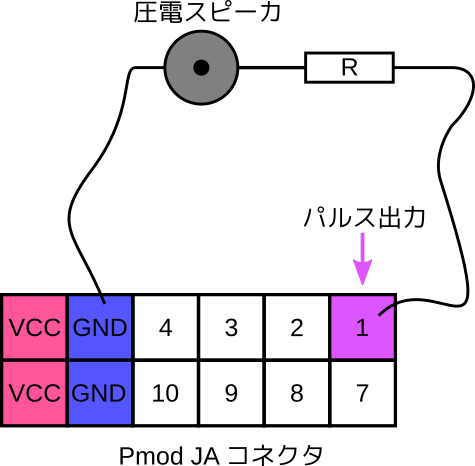
Arty には汎用入出力ポートがたくさんありますが、今回は4つある Pmod 端子のうち Pmod JA の Pin 1 (上段の右端) を使うことにします。圧電スピーカのもう一方の端子は、Pmod JA コネクタの GND に接続します。なお、圧電スピーカには極性はありませんので、どちらの端子をどちらに繋いでも構いません。筆者は下図のようにブレッドボードを使って接続しました。
RTL 記述例
ではパルス波の生成回路を SystemVerilog で記述した例を示します。
`default_nettype none
module pulse_sound
#(
parameter real CLK_FREQ = 100e6, // クロック周波数 (Hz)
parameter int COUNT_WIDTH = 32 // カウンタビット幅
)
(
input wire clk,
input wire [3:0] btn_in,
output logic led_out,
output logic pulse_out
);
// カウンタ増分値の設定: 500 Hz, 1 KHz, 2 KHz, 4 KHz
localparam bit [COUNT_WIDTH-1:0] INCS[4] = '{
freq2inc(500), freq2inc(1000), freq2inc(2000), freq2inc(4000)
};
logic [COUNT_WIDTH-1:0] count = '0;
always @(posedge clk) begin
if (btn_in == '0)
count <= '0; // どのボタンも押されていなければカウンタをクリア
else begin
for (int i = 0; i < 4; i++) begin
if (btn_in[i]) begin
count <= count + INCS[i]; // 押されたボタンに対応する増分値を加える
break;
end
end
end
end
assign pulse_out = count[COUNT_WIDTH-1];
assign led_out = count[COUNT_WIDTH-1];
// 周波数からカウンタの増分値を計算する関数
function bit [COUNT_WIDTH-1:0] freq2inc(real freq);
return ((2.0 ** COUNT_WIDTH) / CLK_FREQ * freq);
endfunction
endmodule
`default_nettype wire他の FPGA ボードにも容易に移植できるように、クロック周波数とカウンタのビット幅は外部からパラメータとして与えられるようにしています。各ボタンが押されたときにカウンタに加える増分値は、定数配列 INCS にまとめています。周波数からカウンタの増分値を求める関数 freq2inc を使って、500 Hz、1 KHz、2 KHz、4 KHz に対応する増分値に初期化しています。関数 freq2inc 内の増分値の計算は real 型で行われますが、増分値は整数ですので return 時に整数に変換されます。ちなみに SysmtemVerilog では real 型から整数型への変換は、小数部の切り捨てではなく丸めが行われます。この増分値の計算は論理合成ツールによって静的に行われますので、この計算を実行するハードウェアが生成されることはありません。real 型を使っていますが、もちろん浮動小数点数演算器が合成されることもありません。
カウンタの動作を記述した always ブロックでは、まず23行目の if で、どのボタンも押されていない場合にはカウンタ値をゼロクリアするようにしています。これはカウンタの停止時に圧電スピーカに直流が加わるのを防ぐ意味もあり、地味に重要な部分です。なお、Arty のボタンの極性はアクティブ High で、押したときに FPGA に「1」が入力されるようなっています。
続く25行目からの else 節では押されたボタンに対応する増分値をカウンタに加えるという動作を for で記述しています。この for は時間方向ではなく空間方向に展開され、for 文全体の処理が1クロックで実行されます。また、ループインデックス i は 0 から順番にボタンの状態を確認していき、押下されたボタンが見つかると対応する増分値をカウンタに加えて break します。したがって、複数のボタンが同時に押された場合には、インデックスが小さいボタンが優先されることになります。パルス出力は先ほどと同様にカウンタの MSB を接続しています。確認用の LED にも同じものを出力しています。
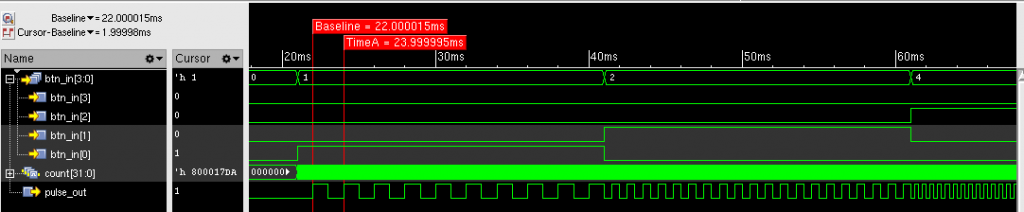
動作確認シミュレーションの波形を次に示します。押したボタンに対応する周波数のパルスが出ていることが確認できます。ただし、例えば500 Hz のパルスは周期が2 ms のはずですが、20 ns ほど足りないようです。これは500 Hz が \( \frac{f_c}{2^{w}} \) で割り切れないことに起因していますが、パルス周期の2 ms はクロック周期10 ns で割りきれますから、本来はきっかり500 Hz のパルスも作れるはずです。今回採用したパルス波生成の手法はとても簡単ですが、このあたりは改善の余地があるといえそうです。
あれ、私の論理合成ツールではエラーになりますが?
はい、そう来るだろうと思っていました。先程のコードは Vivado 2019.2 では合成できるのですが、ツールによっては静的な「事前計算」の部分であっても、real 型を引数にとる関数は合成エラーとなる場合があります。コンパイラやそのバージョンによって文法への対応状況が異なるというのは、ソフトウェアの世界でもままあることですが、ハードウェア記述言語の場合には、シミュレーションでは対応しているが論理合成では未対応というケースもあるので、移植性の問題はなかなか悩ましいところです。
今回はパルス波の周波数を整数値に設定しているので、単に freq2inc の仮引数 freq を int 型とすれば合成できると思います。
function bit [COUNT_WIDTH-1:0] freq2inc(int freq);
return ((2.0 ** COUNT_WIDTH) / CLK_FREQ * freq);
endfunctionピアノの音階の周波数は整数値ばかりではないので、今後の展開を考えるとやや問題がありますが、まあ今回のところはこれでよしとしましょう。
本当は怖い (?) スイッチボタンの話
だいぶ形になってきましたが、もう少しだけ注意すべき点があります。入力に使っているスイッチボタンの取り扱いについてです。
メタステーブルの罠
当然ですが、入力ボタンは人間が好きなときに押します。すると、うっかりクロックの立ち上がりとほとんど同時に押してしまうということも起き得ます。4ビットカウンタでわかる FPGA のための論理回路 入門 (5) でも解説されているように、フリップフロップはクロックの立ち上がりの前後では、入力信号は制止している必要があります。セットアップ制約とホールド制約ですね。
カメラのシャッターを押すときに被写体が制止していないといけないのと同じですが、スイッチボタンのようにクロックと関係ないタイミングで入ってくる入力 (非同期入力) は、そうもいきません。タイミング制約が満たされないと、カメラの場合には撮影した写真がブレてしまいますが、フリップフロップの場合はかなり厄介なことが起きる可能性があります。それがメタステーブルです。
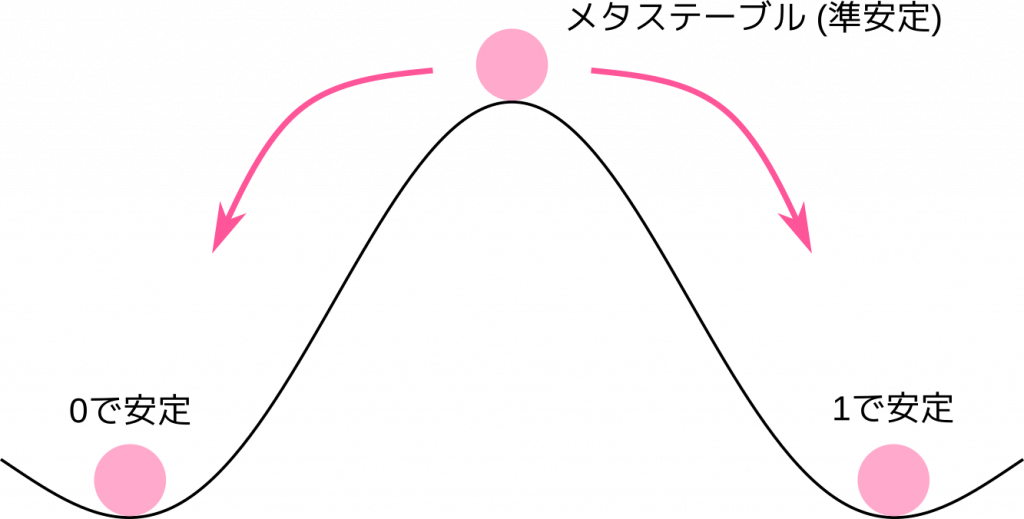
フリップフロップは「0」と「1」の2つの安定状態をもっています。1ビットのデータを記憶できる所以です。しかし、2つの安定状態の中間に、実はもうひとつの状態があるのです。模式的に示したのが次の図です。2つの安定状態の間にポテンシャルの山があり、この頂上でうまくバランスをとると、その状態でとどまることができてしまうのです。
もちろん、ちょっとでもバランスが崩れると、すぐに「0」か「1」のどちらかの状態に落ちてしまいますので、完全な安定状態とはいえません。そこでメタステーブル (準安定) 状態と呼ばれるのです。
フリップフロップがメタステーブル状態になると、その出力は「0」と「1」の間の中途半端な電圧となったり、その間を振動したりしますので、後段の論理の挙動が読めなくなります。さらに問題となるのがファンアウトが2以上だった場合で、同じ信号を参照しているにも関わらず、「0」か「1」の解釈が分かれたりする可能性があります。こうなるとシステムの整合性がまったく保てなくなる可能性があります。
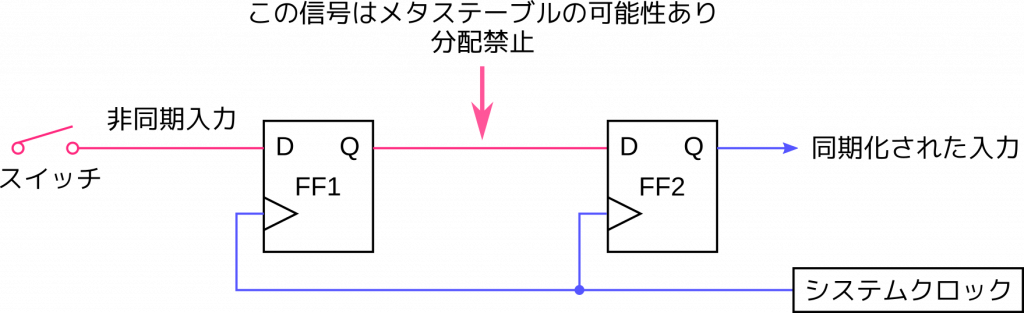
非同期入力によるメタステーブルの問題を完全に排除することはできないのですが、その影響を実質的に無視できるレベルに低下させる方法はいくつか存在します。スイッチボタン入力のような非同期入力を同期化するのによく用いられるのは、以下の図のような2段のフリップフロップを使ったシンクロナイザ (同期化回路) です。
名前は偉そうですが、単なるシフトレジスタです。1段目のフリップフロップ (FF1) は、ノーガードですから当然メタステーブル状態に入る可能性があります。しかし、その出力が2段目のフリップフロップ (FF2) に取り込まれるまでは、1クロックの時間がありますので、それまでには0か1かに落ち着くだろう、というのが原理です。メタステーブル状態が長引き、安定状態への遷移が運悪く次のクロックの立ち上がりと重なってしまうと、FF2 もメタステーブル状態になる、ということも理屈の上ではあり得ます。でも、その確率は無視できるほど低いだろうということです。したがって、クロックの周波数が高い場合や、高い信頼性が要求される場合には、安全のため3段以上にしたりすることもあります。
メタステーブルの問題が厄介なのは、そう頻繁には起こらないことです。特に今回のように人間が押すようなスイッチに対しては、対策をしなくても直ちに困ったことにはならないでしょう。それでも、異なるクロックのシステム間で頻繁に信号をやり取りするときなどは、メタステーブルの問題が顕在することがあります。油断は禁物です。
バウンスの罠
メタステーブルよりも頻繁に顕在化するのがバウンスの問題です。これは、ボタンを押したり離したりする際に、接点が振動的に接触することで、1回のスイッチングにも関わらず0と1を何度も往復した信号が入力されてしまう問題です。この現象はチャタリングとも呼ばれます。
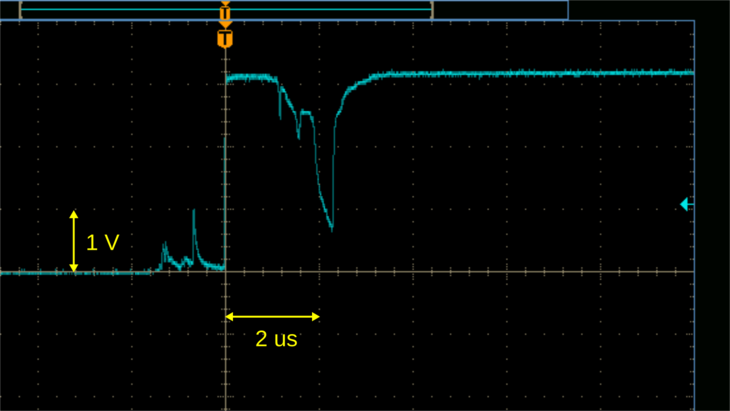
Arty ボードのスイッチボタンを押したときの信号を実際にオシロスコープで見てみました。縦軸の1目盛は1 V、横軸の1目盛は2 us です。ボタンの押し方にもよりますが、この例では、信号が遷移を始めてから安定するまでに5 us くらい要しており、その間はかなりバタついているのが分かります。
ボタンを押している間は音が出るという今回のような回路の場合には、特に対策をしなくてもあまり気にならないと思いますが、例えば、ボタンを1回押すたびに音を出したり止めたりするといった回路の場合には影響が顕著です。ボタンを1回押しただけなのに2回押したと判定され音が出ない、などといったことが起き得ます。
ボタンと FPGA の間に抵抗とコンデンサで構成したローパスフィルタを入れて、バウンスへの対処を不要としているボードもありますが、そうでない場合には何らかの対策が必要となります。例えば入力が変化してもしばらくは保留しておき、一定期間変化がないことを確認してからその入力の変化を取り入れるといった手法が考えられます。
極性の罠
これは笑い話のレベルのようですが、案外うっかりすることが多いです。
ボタンには押したときに1が入力されるもの (アクティブ High) と、押したときに0が入力されるもの (アクティブ Low) があります。今回使っている Arty の4つのボタンはアクティブ High ですが、もう1つの RESET と書かれたボタン (これもユーザ回路で自由に使うことができます) はアクティブ Low です。同じボード上でも混在するくらいですから、設計を他の FPGA ボードに移植する場合には混乱することがあります。どうも回路が動かないと思ったら極性を間違えてリセットがかかりっぱなしになっていた、などというのは筆者の研究室ではよくある話ですので侮れません。
シンクロナイザつきデバウンサ
極性の話はともかく、今後安心してスイッチボタンを使えるように、シクロナイザのついたデバウンサ のモジュールを作っておきましょう。デバウンサというのは、入力のバタつきを取り除いて出力する回路のことです。
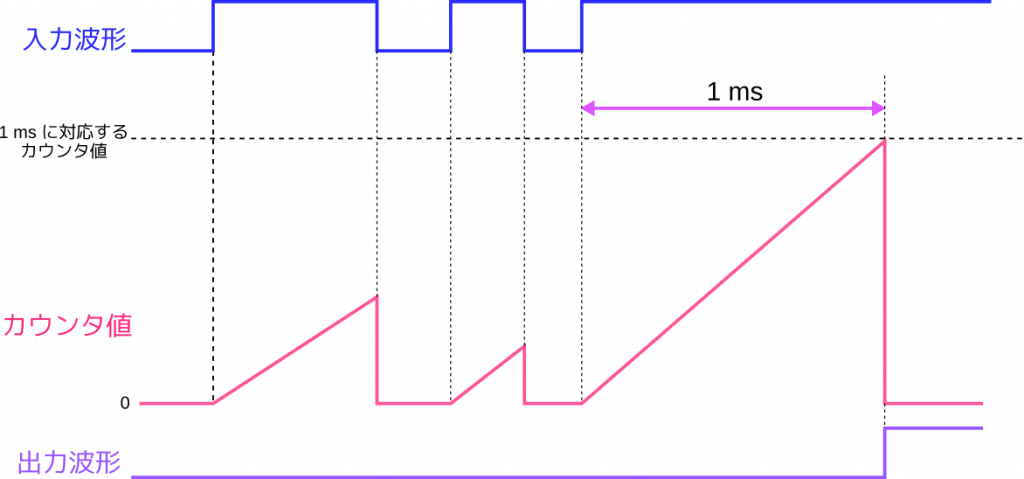
動作の概要は以下の通りです。まず、デバウンサへの入力も、デバウンサからの出力も0のときを考えます。いま、入力が0から1に変化しました。ここで無条件に出力を1にしてしまったら意味がありません。デバウンサは1に変化した入力が本当に一定期間 (ここでは1 ms としましょう) 安定するのかを見届ける必要があります。そのためには1 ms 分のクロックを数えるカウンタがあればよさそうです。もし、無事にカウンタで1 msを測り終えるまで入力が1から変わらなければ、そこで初めて出力を1に変化させます。もし、1 ms 経過する前に入力が0に戻ったら、その時点でカウンタをクリアして振り出しに戻ります。動作を図示するとこんな感じです。
1から0への変化時も同様です。デバウンサの出力が1のときには、0が入力されることがカウントアップの条件になります。1 ms を数え終わるまでに入力が1に戻ってしまったら、カウンタをクリアして始めからやり直しです。
まとめると、カウンタをインクリメントする条件はデバウンサの入力と出力が異なるとき、カウンタをクリアする条件はデバウンサの入力と出力が一致したとき、となります。そして、カウンタの値が1 ms に相当する値に達したら、そこで初めて入力の変化を出力に伝えるということになります。したがって、現在の出力値を記憶しておくための1ビットのレジスタも必要になります。シフトレジスタによるシンクロナイザと合わせて SystemVerilog で記述した例は次に示します。
`default_nettype none
module sync_and_debounce
#(
parameter real CLK_FREQ = 100e6, // クロック周波数 (Hz)
parameter real STABLE_TIME = 1e-3 // 安定したと判定するまでの時間 (秒)
)
(
input wire clk,
input wire din,
output logic dout = 1'b0
);
// 2段のシフトレジスタによるシンクロナイザ
logic din_meta = 1'b0, din_sync = 1'b0;
always @(posedge clk) begin
din_meta <= din; // メタステーブルの危険あり
din_sync <= din_meta; // 同期化された入力信号
end
// デバウンス用カウンタのビット幅と最大値
localparam int COUNT_WIDTH = $clog2(int'(STABLE_TIME * CLK_FREQ));
localparam bit [COUNT_WIDTH-1:0] MAX_COUNT = STABLE_TIME * CLK_FREQ - 1;
// カウンタ
logic [COUNT_WIDTH-1:0] count = '0;
always @(posedge clk) begin
if (din_sync != dout) begin // 入力と出力が異なるならカウンタを進める
if (count == MAX_COUNT)
count <= '0;
else
count <= count + 1'b1;
end
else // 入力と出力が同じならカウンタをクリア
count <= '0;
end
// 出力レジスタ
always @(posedge clk) begin
// カウンタが最大値まで達したら入力の変化を出力に伝える
if (din_sync != dout && count == MAX_COUNT)
dout <= din_sync;
end
endmodule
`default_nettype wire入力が安定したと判断するまでの時間 (先ほどの説明で1 ms としたやつです) とクロックの周波数はパラメータで与えられるようにしています。これらの値から、カウンタの最大値や必要なビット幅を自動で求めるようにしています。もちろん、この計算は合成時に静的に行われます。
17行目の always ブロックがシンクロナイザとして機能するシフトレジスタの記述です。din_sync が同期化された入力信号で、デバウンサはこの信号を参照します。29行目の always ブロックがデバウンサ用のカウンタの記述、41行目の always ブロックが現在の出力値を記憶するレジスタの記述です。先ほどの図と見比べてみると、その動作が分かると思います。
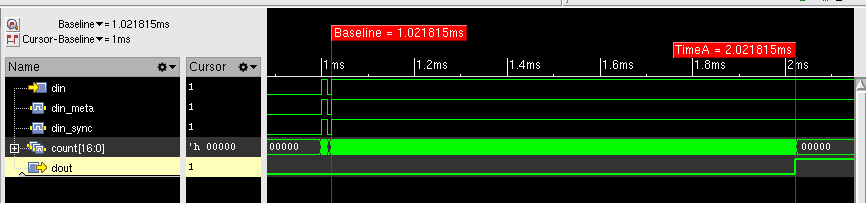
簡単なシミュレーションの結果を以下に示します。出力 dout は入力 din のバウンスに反応することなく、1 ms の安定を待ってから0から1へ遷移しているのが分かります。
トップモジュール作成と実機動作
それでは、今回の設計したモジュールを統合したトップモジュールを作成します。お手持ちのボードのボタンがアクティブ Low の場合には、このトップモジュール内で反転させてやれば、先ほどのパルス波発生のモジュールを変更する必要はありません。以下に記述例を示します。
`default_nettype none
module pulse_sound_artytop
(
input wire clk,
input wire [3:0] btn_in,
output logic led_out,
output logic pulse_out
);
localparam real CLK_FREQ = 100e6; // クロック周波数: 100MHz
logic [3:0] btn_sync; // 同期化されたボタン入力
for (genvar i = 0; i < 4; i++) begin
// シクロナイザつきデバウンサ
sync_and_debounce
#(
.CLK_FREQ(CLK_FREQ),
.STABLE_TIME(1e-3) // 安定判定時間: 1 ms
)
sync_and_debounce_inst
(
.clk(clk),
.din(btn_in[i]),
.dout(btn_sync[i])
);
end
// パルス波発生回路
pulse_sound
#(
.CLK_FREQ(CLK_FREQ),
.COUNT_WIDTH(32)
)
pulse_sound_inst
(
.clk(clk),
.btn_in(btn_sync),
.led_out(led_out),
.pulse_out(pulse_out)
);
endmodule
`default_nettype wireVivado 2019.2 では問題ありませんでしたが、ツールの SystemVerilog への対応状況によっては generate を省略してはいけないとか、genvar の定義位置がおかしいとか、ブロックに名前がないなどといわれてエラーになるかもしれません。そのような場合には、次のように少し保守的な文法で sync_and_debounce モジュールを実体化すれば OK です。
generate
genvar i;
for (i = 0; i < 4; i++) begin : gen_sync_and_debounce
sync_and_debounce
#(
.CLK_FREQ(CLK_FREQ),
.STABLE_TIME(1e-3)
)
sync_and_debounc_inst
(
.clk(clk),
.din(btn_in[i]),
.dout(btn_sync[i])
);
end
endgenerateArty A7-35T 用の IO ピン割り当てファイルを含むソースコードは Gist からダウンロードできます。論理合成が通り、無事にビットストリームが生成されたら、いよいよ FPGA にコンフィギュレーションして試してみましょう。動作の様子を以下に示します。
うまく鳴りましたか? 周波数が異なる、つまり高さが異なる4つの音の鳴動を確認できたと思います。圧電スピーカは特定の周波数に対してよく音が出るように設計されています。今回、筆者が使った PKM17EPP-4001-B0 は4 KHz が定格でしたので、他の音に比べてこの音だけ大きく発音しました。パルス波の周波数を色々と変更して試してみてください。
まとめ
- 0と1のパルスも空気の振動に変えれば音になる
- パルス発生の原理は L チカと同じである
- カウンタの増分値によってパルスの周波数をコントロールできる
- ヘッドフォンを FPGA に直結するのは厳しいが、圧電スピーカなら簡単
- スイッチボタンの扱いには気をつけよう
音を出すのも意外と簡単だなと思っていただけたのではないかと思います。しかし、この回路、いかにも機械的な感じでまったく音楽的じゃないですね。でも、千里の道も一歩から。次回は音階を出したり、ブレッドボード上にアンプを作成してスピーカを鳴らしたりしたいと思います。
長崎大学・柴田 裕一郎