前回はデルタシグマ変調回路を実装して振幅の自由を手に入れました。もはやパルス波じゃなくても出力できます。そこで今回は正弦波を FPGA で生成して出力します。三角関数の計算はどうしましょうか? BRAM でテーブルを作って索く? 確かに定番ですが、他の方法はないでしょうか。 CORDIC? それもありますね。でも、やっぱりテーブルが必要です。今回は題して「テーブルがなくてもできる正弦波出力」。もちろんテーブルを使ったって構わないのですが 、実装の選択肢を色々と持っておくことも何かの時には役に立ちます。
テーブルを使わない正弦波生成
それでは種明かし。ご存知の方もいらっしゃると思いますが、次の連立漸化式によって正弦波が作れます。\[
\begin{align}
f_{n+1} &= f_n + k \cdot g_n \tag{1} \label{f_update}\\
g_{n+1} &= g_n – k \cdot f_{n + 1} \tag{2} \label{g_update}
\end{align}
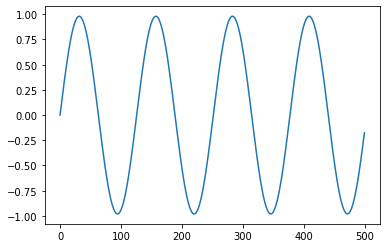
\]本当でしょうか。適当に値を入れて確かめてみましょう。たとえば、係数を \(k = 0.05\) 、初期値を \(f_0 = 0\)、\(g_0 = 0.98\) として \(f_n\) をプロットしてみます。
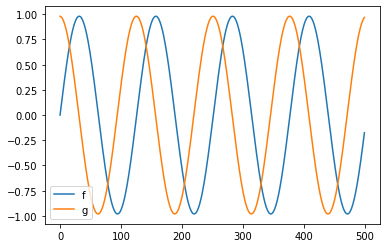
いかがですか? とても簡潔な式から正弦波が生成されました。\(f_n\) に加えて \(g_n\) もプロットするとこんな感じです。
どうやら \(\sin\) と \(\cos\) に対応しているらしいことが分かります。これなら FPGA でも簡単に実現できそうですね。ちなみに振幅がぴったり1になっていないのは、係数や初期値を適当に決めたからで、計算精度の問題ではありません。
原理
しかし、こんなに単純な方法で本当に大丈夫なのか心配の向きもあるでしょう。原理を確認しておきましょう。
sin の微分は cos
周波数 \(F_p\)、振幅 \(A\) の正弦波を考えます。これは時刻を \(t\) とすると、\[
f(t) = A \sin(2 \pi F_p t) \tag{3}\label{f}
\]と表せます。この \(f(t)\) を \(t\) で微分すると、よく知られているように \( \sin\) の微分は \( \cos\) ですから、\[
\frac{df(t)}{dt} = 2 \pi F_p A \cos(2 \pi F_p t)
\]となります。ここで、\[
g(t) = A\cos(2 \pi F_p t) \tag{4}\label{g}
\]と書くことにすれば、\[
\frac{df(t)}{dt} = 2 \pi F_p \cdot g(t)
\]と表せます。
この関係式は時刻 \(\left(t + \frac{\Delta t}{2} \right)\) を中心として\[
\frac{f(t + \Delta t) – f(t)}{\Delta t} = 2 \pi F_p \cdot g \left(t + \frac{\Delta t}{2} \right)
\]のように差分で近似できます。もちろん、\( \Delta t\) は微小な時間です。両辺を \( \Delta t\) 倍して整理すると、\[
f(t + \Delta t) = f(t) + 2 \pi F_p {\Delta t} \cdot g \left(t + \frac{\Delta t}{2} \right)
\]となります。少し見やすくするために、\[
k = 2 \pi F_p {\Delta t} \tag{5}\label{k}
\]と置くと、\[
f(t + \Delta t) = f(t) + k \cdot g \left(t + \frac{\Delta t}{2} \right) \tag{6}\label{fu_org}
\]となります。
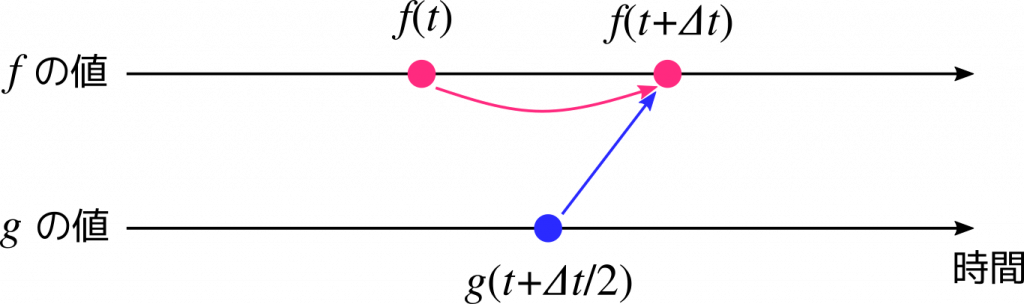
これは、時刻 \( t\) における関数 \(f\) の値と、時刻 \(\left(t + \frac{\Delta t}{2} \right)\) における関数 \(g\) の値 (つまり関数 \(f\) の微分係数) から、時刻 \( (t + \Delta t) \) における関数 \(f\) の値が計算できるということを表しています。このあたり、前回説明したオイラー法の考え方と雰囲気は似ていますね。
cos の微分は -sin
さきほど式 \(\eqref{g}\) として定義したもうひとつの関数\[
g(t) = A \cos(2 \pi F_p t)
\]も微分してみます。\( \cos\) の微分は \(-\sin\) ですから、\[
\frac{dg(t)}{dt} = – 2 \pi F_p A \sin(2 \pi F_p t)
\]です。式 \(\eqref{f}\) で定義したように、\( f(t) = A \sin(2 \pi F_p t) \) ですので、これは\[
\frac{dg(t)}{dt} = – 2 \pi F_p \cdot f(t)
\]と書けます。
この関係式は、時刻 \(t\) における中心差分を使うと\[
\frac{g\left(t + \frac{\Delta t}{2}\right) – g\left(t – \frac{\Delta t}{2}\right)}{\Delta t} = -2 \pi F_p \cdot f(t)
\]のように近似できます。両辺を \( \Delta t\) 倍して整理すると、\[
g\left(t + \frac{\Delta t}{2} \right) = g\left(t – \frac{\Delta t}{2} \right) – 2 \pi F_p \Delta t \cdot f \left(t \right)
\]となります。式 \( \eqref{k} \) において、\( k = 2 \pi F_p {\Delta t}\) と置いたので、\[
g\left(t + \frac{\Delta t}{2} \right) = g\left(t – \frac{\Delta t}{2} \right) – k \cdot f \left(t \right) \tag{7}\label{gu_org}
\]となります。
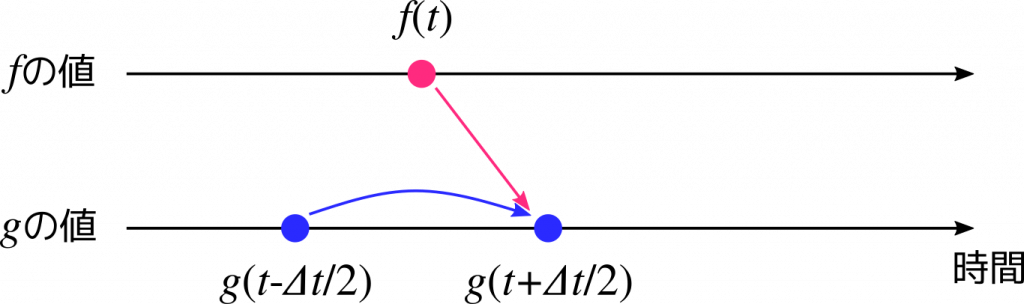
これは、時刻 \( \left( t – \frac{\Delta t}{2}\right)\) における関数 \(g\) の値と、時刻 \(t\) における関数 \(f\) の値から、時刻 \( \left(t + \frac{\Delta t}{2}\right) \) における関数 \(g\) の値が計算できるということを表しています。
連立漸化式の正体
実際のシステムでは時間が離散化されているので、整数 \(n\) を使って \(t = n\Delta t\) と表すことにします。そして、\[
\begin{align}
f_n &= f(n \Delta t) \tag{8}\label{f_n} \\
g_n &= g\left(n \Delta t + \frac{\Delta t}{2} \right) \tag{9}\label{g_n}
\end{align}
\]と表すことにします。さきほど導出した \(f(t + \Delta t)\) の値を計算する式 \(\eqref{fu_org}\) を、この式 \(\eqref{f_n} \) と式 \(\eqref{g_n} \) を使った表記法で置き換えると\[
f_{n+1} = f_n + k \cdot g_n
\]となって冒頭の連立漸化式の1つ目の式 \(\eqref{f_update}\) そのものになります。
同様に \( g\left( t +\frac{\Delta t}{2} \right) \) を計算する式 \(\eqref{gu_org}\) も表記を置き換えると\[
g_n = g_{n-1} – k \cdot f_n
\]となりますが、1ステップ進めると\[
g_{n+1} = g_n – k \cdot f_{n+1}
\]となって、連立漸化式の2つ目の式 \(\eqref{g_update}\) と一致します。
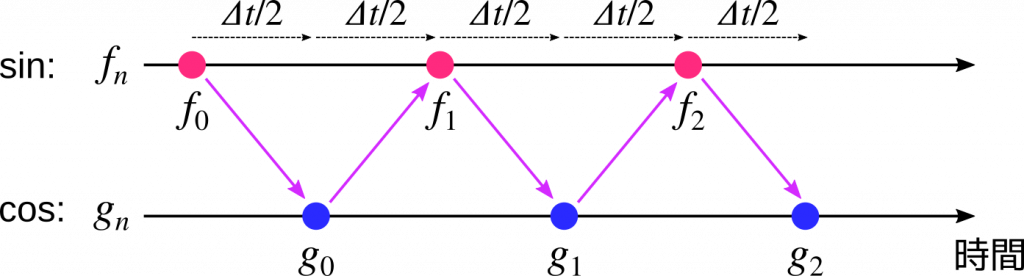
これが連立漸化式の正体です。決してアヤシイものではありません。なお、\(f_n\) と \(g_n\) は添字の \(n\) が同じでも、対応する時刻は \( \frac{\Delta t}{2} \) だけずれていることに注意してください。
リープフロッグ
以上のことから、時計を \( \frac{\Delta t}{2} \) ずつ進めながら、次の2ステップを交互に繰り返せばよいことが分ります。
- 式 \(\eqref{f_update}\) を使って前の \(f\) と \(g\) の値から次の \(f\) の値を求める
- 式 \(\eqref{g_update}\) を使って前の \(g\) と \(f\) の値から次の \(g\) の値を求める
式 \(\eqref{f}\) と式 \(\eqref{g}\) で定義したように、\(f\) は \(\sin\)、\(g\) は \(\cos\) の関数です。つまり、\( \sin\) と \( \cos\) が \( \frac{\Delta t}{2} \) ずつ交互に求まるわけです。
このように時刻をずらしながら交互に数値積分を進めていく方法は、リープフロッグ (leapfrog) 法と呼ばれています。2階の微分方程式を解くのに使われます。たとえば電磁界シミュレーションで使われる FDTD 法もその1つで、磁界、電界、磁界、電界…というように計算が交互に進みます。
直訳すると蛙 (frog) の跳躍 (leap) となるので、「蛙飛び法」などとも訳されますが、英単語としての leapfrog は、かがんだ相手の背中を交互に飛び越えていく遊びのことです。日本語で言えば「馬跳び」です。\( \sin \) と \( \cos \) が馬跳びしていくイメージをつかめたでしょうか?
係数の定め方
原理が分かったところで、漸化式の係数 \( k \) の定め方について考えます。
まず、生成したい波の周波数と振幅は、それぞれ \(F_p\)、 \(A\) です。リープフロッグの時間刻みは \( \frac{\Delta t}{2} \) ですが、今回はこれを1クロックとすることにしましょう。つまり1クロックごとに、\(\sin\)、\(\cos\)…と交互に値を求めていくのです。\(\sin\) だけ見ると、2クロックに1回ずつ値が求まることになります。
クロックの周波数を \( F_c \) とすると、\[
\frac{\Delta t}{2} = \frac{1}{F_c}
\]となるので、\[
\Delta t = \frac{2}{F_c} \tag{10}\label{Delta_t}
\]です。これを式 \(\eqref{k}\) で定義した \( k = 2 \pi F_p {\Delta t} \) に代入すると、\[
k = \frac{4 \pi F_p}{F_c} \tag{11}\label{k_init}
\]となります。係数は生成したい波の周波数とクロック周波数から求まることが分かりました。
初期値の与え方
次に初期値です。 \( f_0\) は簡単です。式 \(\eqref{f_n}\) の \(f_n = f(n \Delta t)\) で \( n=0\) とすると、\[
f_0 = f(0)
\]です。そこで、式 \(\eqref{f}\) の \(f(t) = A \sin(2 \pi F_p t)\) に \(t=0 \) を代入すると、 \[
f(0) = A \sin(0) = 0
\]となります。つまり\[
f_0 = 0 \tag{12}\label{f_0_init}
\] です。
一方、式 \(\eqref{g_n}\) の \(g_n = g\left(n \Delta t + \frac{\Delta t}{2} \right) \) で \(n = 0\) とすると、\[
g_0 = g\left(\frac{\Delta t}{2} \right)
\]となります。そこで、式 \(\eqref{g}\) の \(g(t) = A\cos(2 \pi F_p t) \) に \(t = \frac{\Delta t}{2}\) を代入すると、 \[
g\left(\frac{\Delta t}{2} \right)
= A\cos \left( \pi F_p \Delta t \right)
\]となり、これに式 \(\eqref{Delta_t}\) の \(\Delta t = \frac{2}{F_c}\) を代入すると、結局、\[
g_0 = A\cos \left( \frac{2 \pi F_p}{F_c} \right) \tag{13}\label{g_0_init}
\]を得ます。\(g\) の初期値は、生成したい波の振幅と周波数、そしてクロック周波数から求まることが分かりました。
固定小数点数の演算
理論的な背景が数値積分となると浮動小数点数の演算が必要かと思われるかもしれませんが、この漸化式の計算は固定小数点数でも十分です。正弦波は振幅が決まっていますので、演算に必要なダイナミックレンジはそれほど広くないのです。
ビット幅の検討
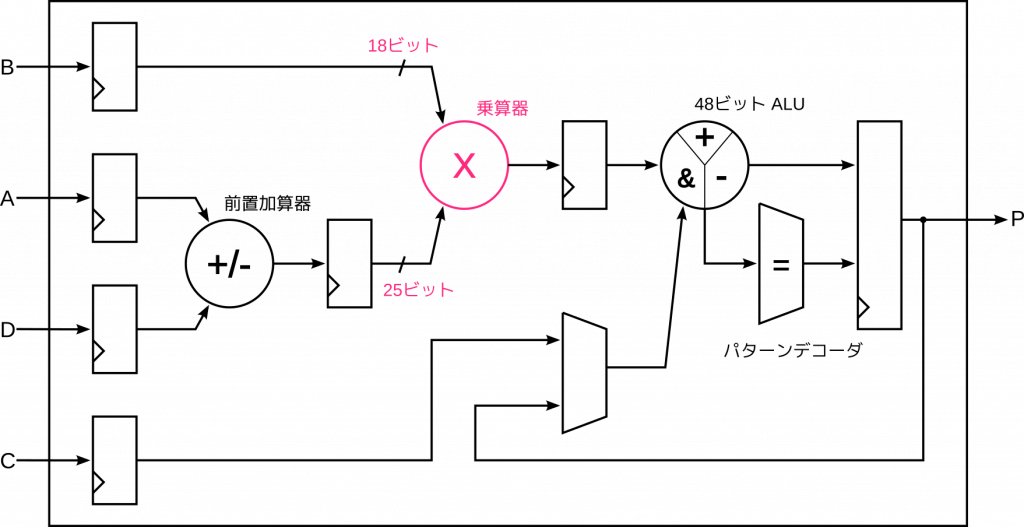
それでは何ビットの固定小数点数にするか検討します。今回の漸化式には符号付きの乗算が必要で、これと加算と合わせて1クロックで実行する計画でした。FPGA での乗算は組み込みの演算資源を使うのが効率的です。次の図は Artix-7 FPGA が提供する DSP スライス (DSP48E1) の構造です。
この図からも分かるように、DSP48E1 スライスでは25ビットと18ビットの符号付き乗算をサポートしています。これを超えるビット幅だと1個の DSP スライスでは乗算を実現できません。そこで今回は、\(f_n \) と \(g_n\) は25ビット、\(k\) は18ビットの固定小数点数として表すことにします。
小数点の位置
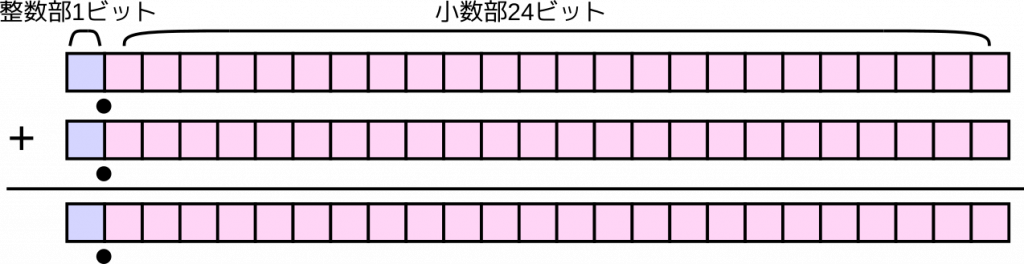
\(f_n\) と \(g_n\) のとる値の範囲は、振幅 \(A\) で決まります。具体的には、式 \(\eqref{f}\) と式 \(\eqref{g}\) から分かるように、最小値は \(-A\)、最大値は \(+A\) です。そこで、\(A\) の値には \(1\) 未満の値を設定することとし、\(f_n\) と \(g_n\) の小数点は MSB の右隣に置くこととします。つまり、整数部は1ビット、小数部は24ビットとします。
負数は2の補数で表します。したがって、この25ビットで表すことのできる値の範囲は \(-1\) 以上 \(+1\) 未満となります。ぴったり \(+1\) は表せません。どうしても \(+1\) を表現したいなら整数部を2ビットとる必要がありますが、そうすると \(-1\) から \(-2\) までの表現力が無駄になってしまいます。さきほど \(A\) の値の範囲を \(1\) 以下ではなく、\(1\) 未満としたのは、\(f_n\) や \(g_n\) の値がぴったり \(+1\) にならないようにするためです。
小数点を置くといっても、もちろん人間がそう思うだけであって、実際のデータには小数点は現れません。ハードウェアから見ると整数値と変わりません。特に加減算では、2つのオペランド (加数と被加数) の小数点の位置が同じであれば、整数演算とまったく同じ回路になります。
乗算では小数点が動く
乗算の場合は、筆算のときと同様に、小数点の位置がどこにくるか意識しないといけません。
例として25ビットと18ビットのデータの乗算について考えます。25ビットのデータは整数部が1ビットで小数部が24ビットだとします。18ビットのデータは整数部が4ビットで小数部が14ビットだとします。
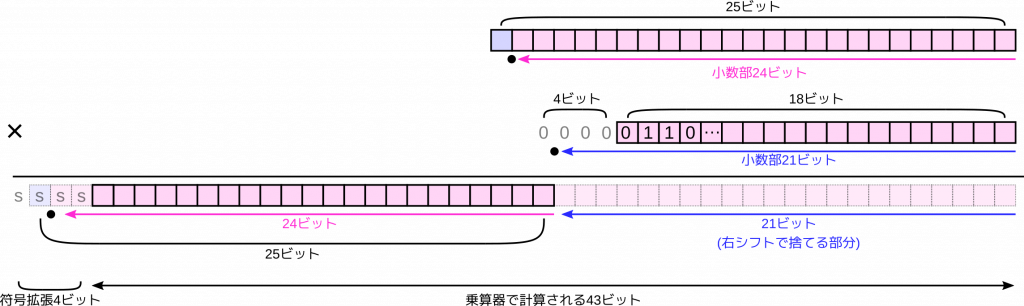
すると次の図のように、25ビットと18ビットの積は合計43 (= 25 + 18) ビットになりますが、小数点は下から(24 + 14) ビット目に来ます。筆算と同じです。この乗算結果を元の25ビットの固定小数点数の形式で表すには、下位の14ビットは捨てることになります。これは乗算結果を14ビット右にシフトするのと同じです。
位取りの工夫
ところで、式 \(\eqref{k}\) で定義したように \(k = 2 \pi F_p {\Delta t}\) です。微小時間 \(\Delta t\) を含むことからも分かるように、\(k\) は絶対値の小さな正の値です。特に正弦波の周波数 \(F_p\) が低いほど絶対値も小さくなります。このような場合、小数点の位置を18ビットの外側にとることで、実質の有効桁数を増やすことができます。
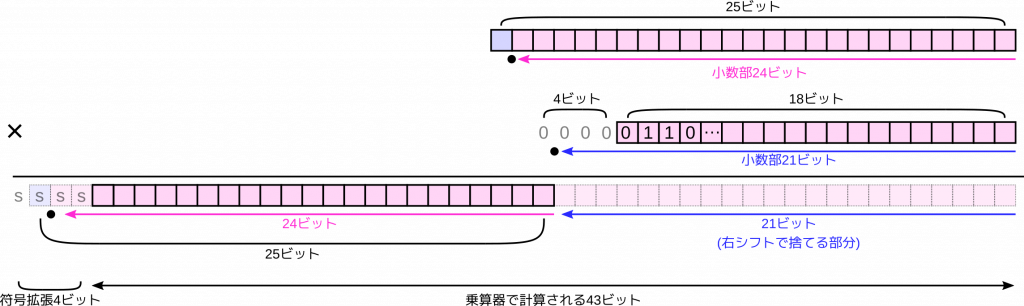
たとえば、\(k\) の値が小数第4位まで0だったとします。ここで小数部の幅を21ビットにしてみます。つまり小数点を18ビットの外側にとるのです。当然、18ビットに収まらずに溢れるビットがでてきます。でも次の図のように、溢れたビットはすべて0だと分かっています。本当は存在していませんが「あるつもり」と考えることができます。
このように、小数点の位置を外側にとることで、本当は18ビットしかないのに、実質的には22ビット分の情報を表すことが可能になります。
この形式で乗算するとどうなるかを考えてみます。乗算器は25ビットと18ビットのデータを先ほどと同じように乗算し、43ビットの積を出力します。これを元の25ビットの形式に戻すには、乗数 \(k\) の小数部の幅だけ右シフトして捨てれば良いのでした。今回は21ビットの右シフトになります。
ただ、これでは乗算結果の上位側のビット (図中の s で現されたビット) の計算がされないと心配になるかもしれません。でも、大丈夫です。これらのビットは乗算結果を符号拡張するだけで求まるのです。要は乗算結果が正の値なら s のビットはすべて0、乗算結果が負の値なら s のビットはすべて1です。
このようにして、この例では25ビットと18ビットの乗算器を使いながら、実質的に25ビットと22ビットの計算をしたのと同じことになりました。
正規化時には符号に注意
以上のことから、絶対値が小さな値については、MSB が1になるように小数点の位置を工夫するのが、有効桁数を増やす上で最良であることが分ります。このような処理を正規化といい、これを演算のたびにやるのが浮動小数点数です。固定小数点数では実行中は小数点の位置をずらせませんが、\( k \) のような定数については、あらかじめ正規化しておくと有利です。
では、\(k \) の値は18ビットで正規化するのがいいのかというと、そうでもありません。というのは、MSB を1にすると乗算器が負の数と判定してしまうからです。\(k\) のように正の値の場合には17ビットで正規化し、先頭から2ビット目に1がくるように小数点の位置を定めるのがよいでしょう。
正弦波生成モジュールの実装
演算の構造
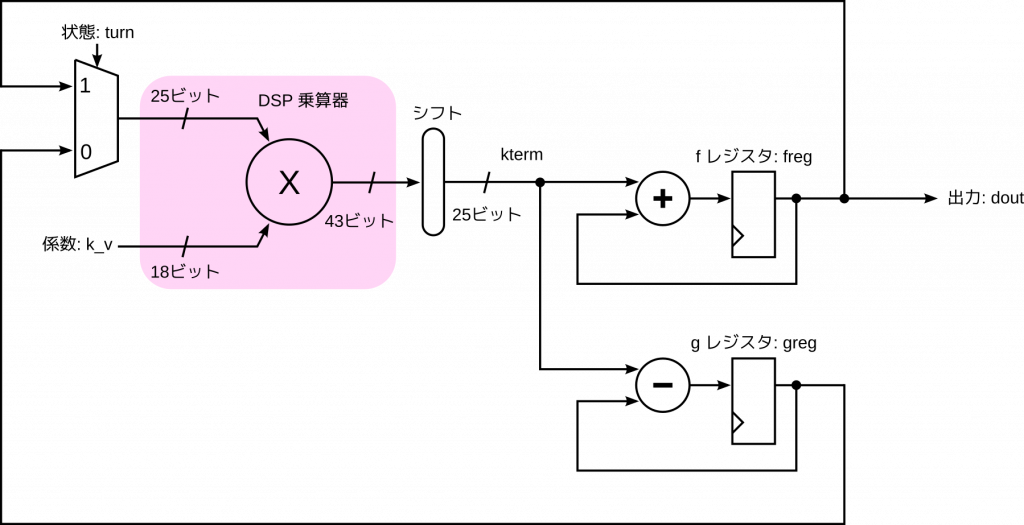
それでは正弦波生成モジュールの実装です。まず構成図を示します。
レジスタとして漸化式の \(f_n\) の値を保持する f レジスタ (freg) と、\(g_n\) の値を保持する g レジスタ (greg) を用意します。さきほど検討したように、それぞれ25ビット幅で、整数部は1ビット、小数部は24ビットです。
また、図示はしていませんが、リープフロッグの動作を制御するために、1ビットの状態レジスタ turn を用意します。これは1クロックごとに0と1の値を交互にとります。turnが0のときには式 \(\eqref{f_update}\) にしたがって f レジスタの値を計算して更新し、turnが1のときには式 \(\eqref{g_update}\) にしたがって g レジスタの値を計算して更新します。
DSP スライスの乗算器は1つだけ使用することにし、f レジスタの計算と g レジスタの計算とで共有します。つまり乗算器は毎クロック休むことなく働きます。乗算器の入口のマルチプレクサは、f の計算のときと g の計算のときとで乗算器の入力を切り替えるためのものです。
出力 dout は f レジスタの値をそのまま出します。クロック以外の入力はありません。クロックが入る限り、ずっと正弦波を出力し続けます。
記述例
SystemVerilog による記述例を示します。
`default_nettype none
module sine_wave_generator
#(
parameter real CLK_FREQ = 100e6, // クロック周波数 (Hz)
parameter int WIDTH = 25, // データビット幅
parameter int K_WIDTH = 18, // 係数 k のビット幅
parameter real TARGET_FREQ = 100, // 生成波の周波数
parameter real AMP = 0.98 // 生成波の振幅 ( < 1)
)
(
input wire clk,
output logic [WIDTH-1:0] dout
);
localparam real PI = 3.14159265358979323846; // 円周率
localparam real K = 4.0 * PI * TARGET_FREQ / CLK_FREQ; // 係数 k
localparam real G0 = AMP * $cos(2.0 * PI * TARGET_FREQ / CLK_FREQ); // 初期値
localparam int K_Q = calc_shift_amount(K, K_WIDTH - 1); // k の小数部ビット幅
localparam bit signed [K_WIDTH-1:0] K_V = K * (2.0 ** K_Q); // 正規化された k
logic signed [WIDTH-1:0] freg = '0; // sin レジスタ
logic signed [WIDTH-1:0] greg = G0 * (2.0 ** (WIDTH-1)); // cos レジスタ
logic signed [WIDTH-1:0] kterm; // 係数 k の乗算結果
logic turn = 1'b0; // 状態レジスタ
// クロックごとに状態を交代
always @(posedge clk) begin
turn <= !turn;
end
// 乗算
assign kterm = ((K_WIDTH+WIDTH)'(K_V) * (!turn? greg: freg)) >>> K_Q;
// レジスタ更新
always @(posedge clk) begin
if (!turn)
freg <= freg + kterm;
else
greg <= greg - kterm;
end
// 出力
assign dout = freg;
// 数値 x を width ビットで正規化するのに必要なシフト量を求める関数
function int calc_shift_amount(real x, int width);
longint t;
int q;
for (t = x, q = 0; !t[width-1] && q < 128; q++) // シフトの最大値を128に制限
t = x * (2.0 ** (q + 1));
return q;
endfunction
endmodule
`default_nettype wireパラメータが多く、係数や初期値の計算の部分も多いので、やや複雑に見えるかもしれませんが、ハードウェアの動作を記述しているところは28行目から44行目までです。記述について何点か補足します。
係数の正規化
係数 \(k\) を正規化するためのシフト量は、47行目の関数 calc_shift_amount を使って求めています。この関数は論理合成ツールによって静的に実行されるだけで、この動作を実現するハードウェアが合成されるわけではありません。
やっていることは、愚直に先頭ビット (t[width-1]) が1になるまでシフト量を順に増やしているだけです。$realtobits を使って real 型の表現の指数部を直接読むなどの方法もありそうですが、移植性の点で問題かもしれません。51行目の q < 128 の条件は、x の値がほぼ0だったときなどに、この for 文が無限にループするのを防ぐためのものです。
19行目でこの関数を呼び出す際に、第2引数を K_WIDTH (18ビット) ではなく K_WIDTH-1 (17ビット) にしているのは、先述のように先頭ビットが1になって乗算器が負の数と判定するのを防ぐためです。
固定小数点数の乗算にはビット幅キャスト
33行目で固定小数点数の符号付き乗算を行っていますが、ここは少し注意が必要です。ありがちなミスが、
assign kterm = (K_V * (!turn? greg: freg)) >>> K_Q;としてしまうものです。SystemVerilog のツールは乗算のオペランドと結果の格納先のビット幅を見て、演算のビット幅を決定します。この場合、kterm は WIDTH ビットですので、乗算の積も WIDTH ビットまでしか求めません。したがって、K_Q ビット右シフトしても積の上位ビットは出てこないので、計算が合わなくなります。
これを防ぎ、ちゃんとすべてのビットの乗算結果を計算してもらうには、ビット幅キャストの文法を使って (K_WIDTH+WIDTH)'(K_V) とする必要があるのです。
符号付き数には算術シフト
もうひとつありがちなミスは、
assign kterm = ((K_WIDTH+WIDTH)'(K_V) * (!turn? greg: freg)) >> K_Q;というものです。「>>」は論理シフトを意味するため、負の数をシフトしても上位から0が入ってきます。すると正の数になってしまいますので、計算が合わなくなります。
算術シフトの「>>>」を使えば、負の数の場合には上位から1が入ります。もちろん正の数の場合には、論理シフトと同様に0が入ります。つまり符号拡張されるのです。なお、「>>>」を使っても、シフトされる対象が signed で宣言されていないと算術シフトにならないので注意が必要です。
演算器の共有
ところで、kterm という中間論理を置かずに36行目からの always ブロックを、
always @(posedge clk) begin
if (!turn)
freg <= freg + (((K_WIDTH+WIDTH)'(K_V) * greg) >>> K_Q);
else
greg <= greg - (((K_WIDTH+WIDTH)'(K_V) * freg) >>> K_Q);
endとするのはどうでしょうか。この方が記述がシンプルです。
シミュレーションすると分かりますが、計算自体はまったく問題ありません。ただ、Vivado はこの記述から DSPスライス を2個推論します。つまり、2つの乗算器が合成され、それぞれ1クロックおきに動作と休眠を繰り返す回路になるのです。乗算器の共有は行われません。
それでも構わない場合もあるでしょうし、やはり演算資源を節約したい場合もあるでしょう。どちらの記述がいいとは一概には言えません。同じ動作を実現する回路でも、その記述によって回路構造が大きく変わる可能性のあることには留意しておく必要があります。
デルタシグマ変調との結合
それでは今回設計した正弦波生成のモジュールと前回設計したデルタシグマ変調のモジュールを結合して動作を確認します。
テスト回路の構成
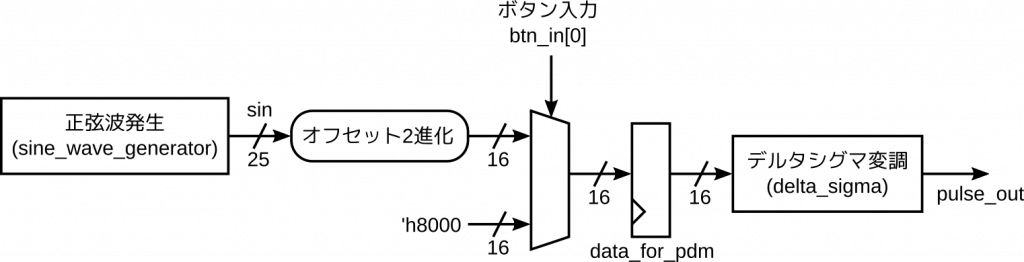
テスト回路 (sine_sound モジュール) は次のようなもので、ボタンを押すと正弦波がデルタシグマ変調されて出力されるだけです。
ちなみに正弦波生成モジュールはボタンとは連動しておらず、クロックが入力される限りずっと正弦波を出力し続けます。ボタンはその出力をデルタシグマに接続するかどうかをスイッチするだけ、というちょっと乱暴な設計です。正弦波の周波数は440 Hz、振幅は0.98に設定しています。
Arty A7-35T 用のトップモジュールやシミュレーションモジュール、IO ピン割り当てファイルなどを含むすべてのソースコードは Gist からダウンロード可能です。
符号付き数から符号なし数への変換
前述のとおり、正弦波発生モジュールが出力するデータ (sin) は25ビットの符号付き固定小数点数です。一方、デルタシグマ変調モジュールの入力データ (data_for_pdm) は16ビットの符号なし整数です。
25ビットを16ビットにするのは、上位の16ビットをとれば良いとして、符号付き数から符号なし数へ変換するには、オフセットを加えて値を一律に持ち上げて、負の数も正の数にする必要があります。これは MSB を反転させるだけで実現できます。この処理はオフセットとして「MSB だけが1の数」を加えたことと等価です。
この部分の SystemVerilog による記述例を示します。
always @(posedge clk) begin
if (btn_in[0]) // ボタン押下なら正弦波をオフセットバイナリへ変換
data_for_pdm <= {~sin[SINE_WIDTH-1], sin[(SINE_WIDTH-2)-:(PDM_WIDTH-1)]};
else // 固定値 (MSB だけ1)
data_for_pdm <= 1'b1 << (PDM_WIDTH-1);
endここで SINE_WIDTH は sin のビット幅 (25ビット)、PDM_WIDTH は data_for_pdm のビット幅 (16ビット) を示すパラメータです。ボタンが押されていないときは、デルタシグマ変調には固定値が入力されます。この固定値は、正弦波出力が0のときと同じ値になるように、MSB だけを1にした値にしています。
シミュレーション
それでは簡単なシミュレーションで動作を確認します。シミュレーションモジュールは前回とほぼ同一で、RC 回路の数値解析モデルも含んでいますので、ローパスフィルタを通った後のアナログ値を観察できます。
見事な正弦波が現れました。周期と振幅も良さそうです。出だしが不連続になっているのは正弦波生成とボタンが連動していないからです。
これで、今回の正弦波生成モジュールが意図どおり動作していることと合わせて、前回のデルタシグマ変調モジュールの動作も問題ないことが確認できました。
実機動作確認
それでは合成して実機での動作も確認してみます。1クロックで乗算、シフト、加算が行われますが、合成の結果、予定通り DSP スライスの乗算器が使われて 100 MHz のタイミング制約を満足することができました。
なお、試しにソースコードのパラメータを書き換えて、正弦波のデータ幅を25ビットから26ビットに増やしてみたところ、DSP 乗算器が推論されずタイミング制約を満たしませんでした。次の表はビット幅を変更した際の資源使用数 (正弦波生成モジュールのみの数値) と Worst Negative Slack をまとめたものです。
| データビット幅 | LUT 使用数 | FF 使用数 | DSP 使用数 | Worst Negative Slack (ns) |
| 25 | 64 | 51 | 1 | 1.066 |
| 26 | 360 | 53 | 0 | -0.294 |
たった1ビット増やしただけなのですが、26ビットにすると LUT 使用数が一気に増えています。これは乗算器が LUT で合成されたためで、これがタイミング制約を満たせなかった原因です。もちろん、ソースコードにプラグマを挿入したり、合成オプションを工夫することで対処する手もありそうですが、いずれにせよ FPGA では演算資源の割り当てを意識した設計が重要であることが分かります。
一方、さきほど図示したように DSP スライス内部には乗算器だけでなく、加算器やレジスタなども入っていますが、それらは一切使われていません。ここには改善の余地があるといえます。もう少しこれらを有効に利用できると LUT や FF の使用数も削減できそうです。ただし、今回の演算構造を変更する必要もありそうです。
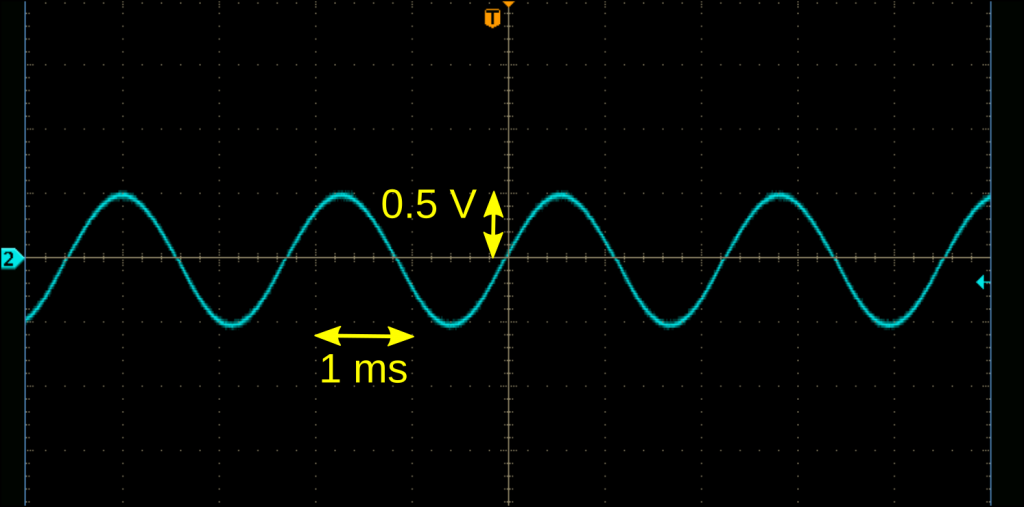
次に実機で動作させ、オシロスコープでローパスフィルタと入力カップリングコンデンサを通った後の波形を確認してみました。
帯域制限で高周波ノイズをカットしていますが、期待した波形が安定的に出力されることが実機でも確認できました。整数演算と1ビットのディジタル出力だけでも、ここまでできるのは楽しいですね。実際の動作の様子は次の通りです。
動画では音を取り込むためにアンプのボリュームをかなり上げているのですが、パルス音と比べると音は小さいです。第2回で見たようにパルス音はさまざまな周波数成分を含んでいるのに対し、正弦波音は単一の周波数だからです。
まとめ
- テーブルを使わなくても簡単な漸化式で正弦波を出力できる
- 原理は2階の微分方程式の数値解法と同じ
- 固定小数点数は小数点の位置の工夫が重要
- ビット幅キャストや算術シフトを忘れずに
- FPGA の演算資源割り当てを意識しよう
今回のテスト回路の動作は地味ですが、技術的には達成感がありました。次回はいよいよ最終回。正弦波生成回路を FPGA ピアノに統合し、音を重ねてポリフォニーの世界への扉を開きます。
(おまけ)
連立漸化式ではなく、単一の漸化式で正弦波を生成する方法もあります。導出には三角関数の加法定理、 \[
\sin(\alpha \pm \beta) = \sin\alpha \cos\beta \pm \cos\alpha\sin\beta
\] を使います。
まず、\(f(t+\Delta t)\) を加法定理を使って展開すると、\[ \begin{align}
f(t + \Delta t) &= A \sin\left(2 \pi F_p (t + \Delta t)\right)\\
&= A \sin ( 2 \pi F_p t) \cos ( 2 \pi F_p \Delta t) +
A \cos ( 2 \pi F_p t) \sin ( 2 \pi F_p \Delta t)\\
&= f(t) \cos ( 2 \pi F_p \Delta t) + A \cos ( 2 \pi F_p t) \sin ( 2 \pi F_p \Delta t) \tag{14}\label{tpd}
\end{align}
\]となります。次に、\(f(t-\Delta t)\) についても同様に加法定理を適用すると、\[ \begin{align}
f(t – \Delta t) &= A \sin\left(2 \pi F_p (t – \Delta t)\right)\\
&= A \sin ( 2 \pi F_p t) \cos ( 2 \pi F_p \Delta t) –
A \cos ( 2 \pi F_p t) \sin ( 2 \pi F_p \Delta t)\\
&= f(t) \cos ( 2 \pi F_p \Delta t) – A \cos ( 2 \pi F_p t) \sin ( 2 \pi F_p \Delta t) \tag{15} \label{tmd}
\end{align}
\]となります。
ごちゃごちゃしてきましたが、ここで式 \(\eqref{tpd}\) と式 \(\eqref{tmd}\) の和をとると、うまい具合に項が相殺され、\[
f(t + \Delta t) + f(t – \Delta t) = 2f(t)\cos ( 2 \pi F_p \Delta t)
\]となります。移項して少し順番を入れ替えると、\[
f(t + \Delta t) = 2\cos ( 2 \pi F_p \Delta t)f(t) – f(t – \Delta t)
\]となります。ここで係数を \( \lambda = 2\cos ( 2 \pi F_p \Delta t) \) と置き、式 \( \eqref{f_n} \) の \( f_n = f(n \Delta t)\) を使って表すと、\[
f_{n+1} = \lambda \cdot f_n – f_{n-1}
\]という三項間漸化式が得られます。これも有名な漸化式です。
長崎大学・柴田 裕一郎