こんにちは。広島市立大学の窪田です。前回、CG 法のプログラムを FPGA 上で実行できるようにしました。今回は、この FPGA 上で実行されるカーネルの高速化を試みます。前回使ったプログラムは github 上のsolver/cg_ocl_base ディレクトリから、今回高速化したプログラムは solver/cg/ocl_ell_lf2 ディレクトリから取得できるようにしました。
回路の合成
Vitis の GUI の統合環境を使って C/C++ のプログラムを build していると、ソフトウェアをコンパイルするのとあまり違いが感じられないかもしれませんが、実際には FPGA 上で実行されるカーネルの論理回路が合成されているということになります。カーネルの高速化を試みる前に、どんな回路が合成されているのか、その確認方法を見ていきます。
Vitis Analyzer による回路合成情報の確認
Vitis では、C/C++ で記述された各関数やループの実行時間や、合成した回路の規模などの情報を確認することができます。Vitis の GUI で前回の CG 法のプロジェクトを開き、以下のような手順で回路を情報を確認してみます。
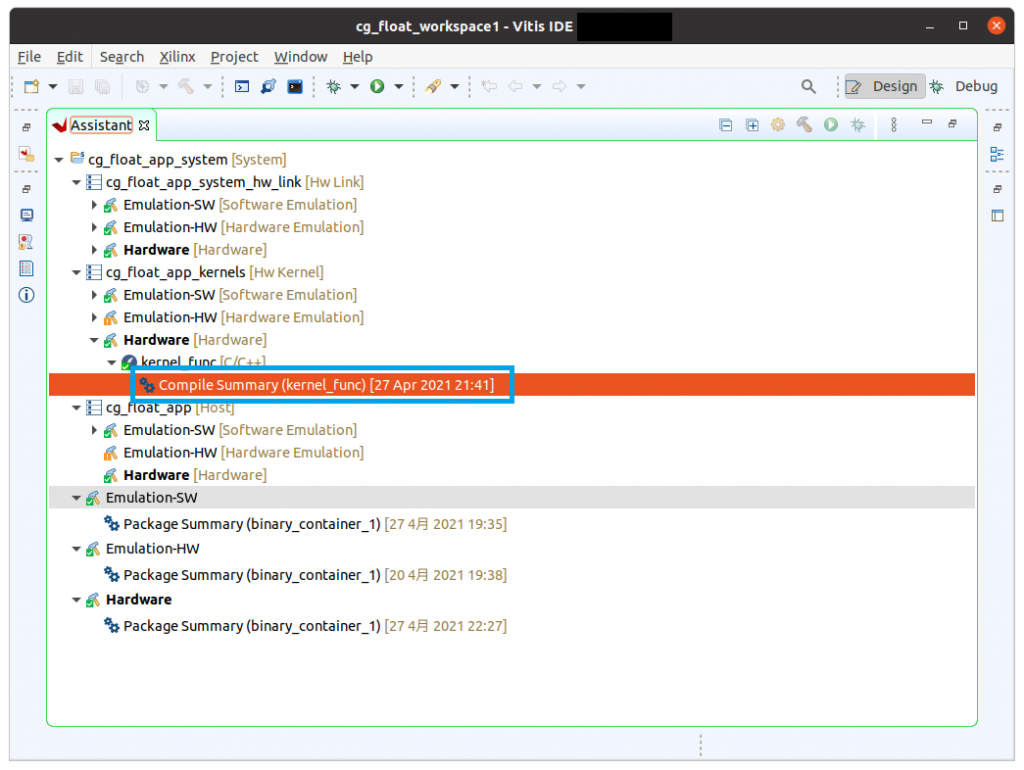
図1のように Assitant タブで階層をたどり、Compiler Summary をダブルクリックして下さい。Compiler Summary までの階層は以下のようになっています。
- cg_float_app_system [System]
- cg_float_app_kernels
- Hardware
- kernel_func
- Compiler Summary [Kernel_func]
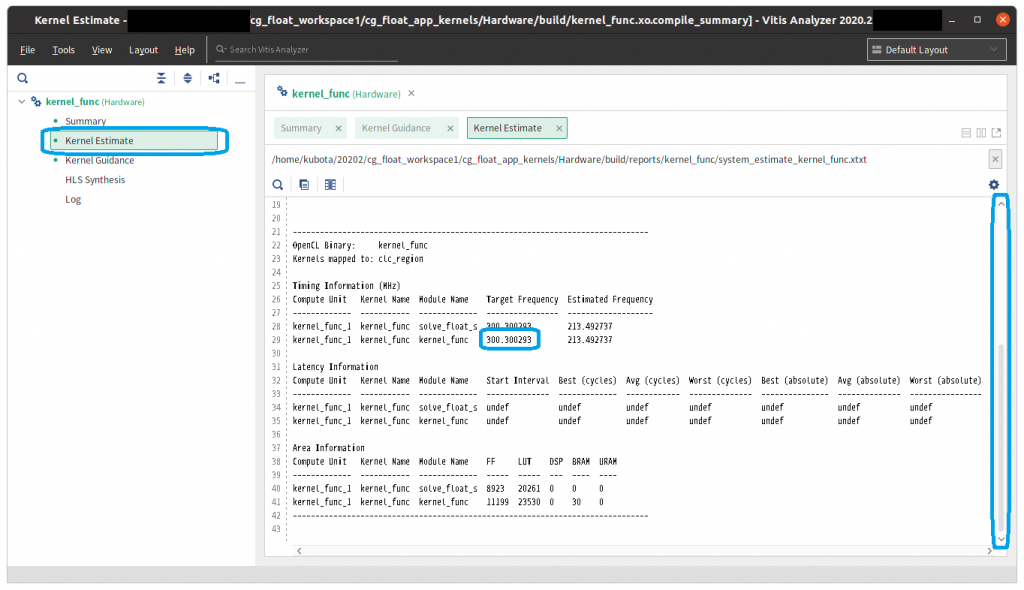
少し時間がかかりますが Vitis Analyzer という新しいウィンドウが現れますので、左側にある Kernel Estimate という文字列をクリックして下さい。図2のような画面が現れます。ウィンドウの右側にカーネルの実行時間 (Latency; 遅延) や回路規模の情報 (FF, LUT, DSP, BRAM など) が表示されますので、適宜スクロールしながら確認して下さい。この回路は 300MHz で動作するように合成されたことも確認できます。
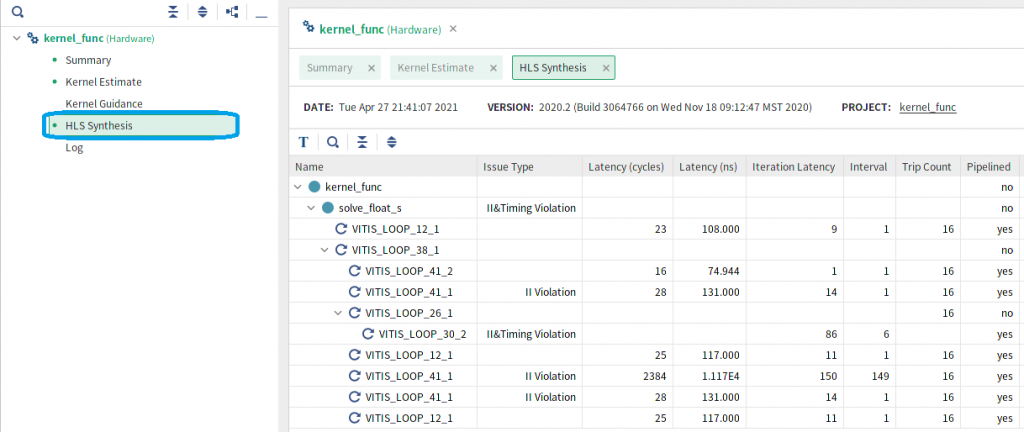
次に、ウィンドウの左側の HLS Synthesis という文字列をクリックしてみましょう。今度は図3のように、各関数の実行時間 (遅延) の一覧が表示されます。
行数が短い関数はツールがインライン化して処理しますので、このウィンドウには現れていない関数名もあります。この CG 法の例では、kernel_func と solve_float_s という関数のみ回路の合成結果が表示されており、dot, spmv, axpy などの関数はインライン化されていることがわかります。なお solve 関数は template 機能使ってデータ型を float として使用していますので、関数名が solve_float_s という名前になっていることに注意して下さい。
ループは VITIS_LOOP_12_1 など、ソースファイル中の行番号などを使った名称になっています。ループにラベルを付けるともう少しわかりやすいループ名になるようです。各ループについて以下のような情報が得られます。
- Latency (cycle): ループ全体の遅延 (単位はクロックサイクル)
- Latency (ns): ループ全体の遅延 (単位はナノ秒)
- Iteration Latency: ループの1反復の遅延
- Interval: ループの各反復の投入間隔
- Trip Count: ループの繰り返し回数
- Pipelined: ループがパイプライン化されているか否か
Vitis では、パイプライン化が適用可能なループはデフォルトでパイプライン化されます。ここで、Iteration Latency を d, Interval を i, Trip Count を n とおくと、パイプライン化されたループの Latency (cycle) l は以下のようになります (一部例外もあるようです) 。
l = i × n + (d – i – 1)
また、HLS Synthesis のウィンドウ内で右にスクロールすると、以下のように各関数の回路で使用されている資源数の情報も得られます。
上が kernel_func 関数、下が solve_float_s 関数の使用資源数です。FPGA の資源は、LUT (Look-Up Table) が論理ゲート、FF (Flip-Flop) が記憶素子、BRAM (Block RAM) が FPGA 内部のメモリ、DSP (Digital Signal Processor) が FPGA 内にあらかじめ用意されている演算器となります。それぞれの使用資源数と、その使用可能な資源数に対する割合が表示されています。この CG 法の回路は少量の資源しか使用していないことがわかります。
CG 法のような浮動小数点演算主体の回路では、浮動小数点の仮数部の演算に DSP、配列変数は BRAM が割り当てられているようです。
Emulation-HW による回路合成情報の見積もり
前回、CG 法のプログラムに対して Emulation-SW と Hardware の2通りの build を行いましたが、Vitis では Emulation-HW という build 方法も可能です。それぞれ以下のようにカーネルを実行、あるいはエミュレーションします。
- Emulation-SW: カーネルのプログラムをホスト上で実行します。
- Emulation-HW: カーネルの FPGA の回路の動作をホスト上でエミュレーションします。
- Hardware: カーネルを FPGA で実行します。
なお、Emulation-HW で build すると、Hardware での build と同様、C/C++ で記述された各関数や各ループの遅延、使用資源量などの情報が得られます。
Hardware での build は数十分から数時間かかるのに対し、Emulation-HW での build は比較的短時間で終了します。CG 法のプログラムの場合で試したところ、Hardware の build が40分程度なのに対して、Emulation-HW の build は5分程度で終了しました。
そこで、カーネルの高速化を試みる場合、C/C++ の記述方法を変えては Emulation-HW で遅延や使用資源量を確認するという手順を繰り返すことで、効率的にカーネルの高速化を行うことができます。次のセクションでいくつかの高速化手法を試しますが、その際にも Emulation-HW で見積もった遅延情報を活用しています。
このセクションの最後に、Emulation-HW で build した場合のエミュレーションの方法についても簡単に説明しておきます。Emulation-SW では環境変数 XCL_EMULATION_MODE を sw_emu に設定しましたが、Emulation-HW では hw_emu に設定します。
export XCL_EMULATION_MODE=hw_emu設定後にホストプログラムを実行してみます。
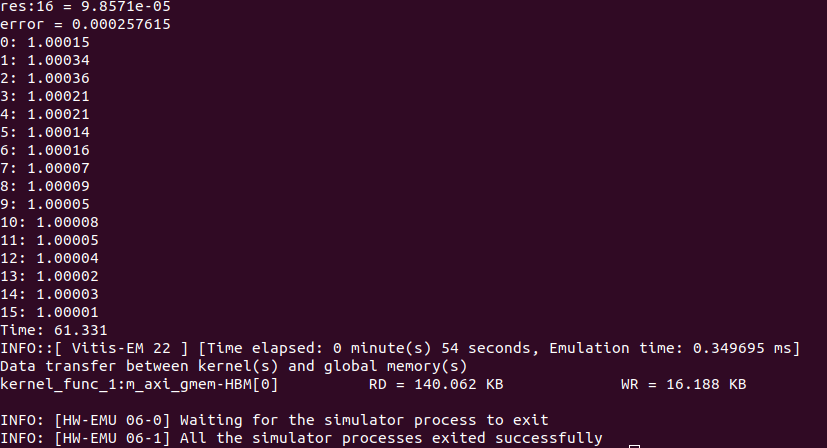
Emulation-HW では、カーネルの回路をホスト上でエミュレーションし、必要に応じてデバッグのための信号波形も出力できますが、その分、Emulation-SW や Hardware の実行に比べると実行時間が長くなります。図5はエミュレーション実行時のメッセージですが、これによると、エミュレーション時間が長くなるのを避けるためか、エミュレーション時には小さいサイズのデータの使用が推奨されています。
実行結果は図6のようになり、Hardware と同じ結果が得られることが確認できました。
CG 法のカーネルの高速化
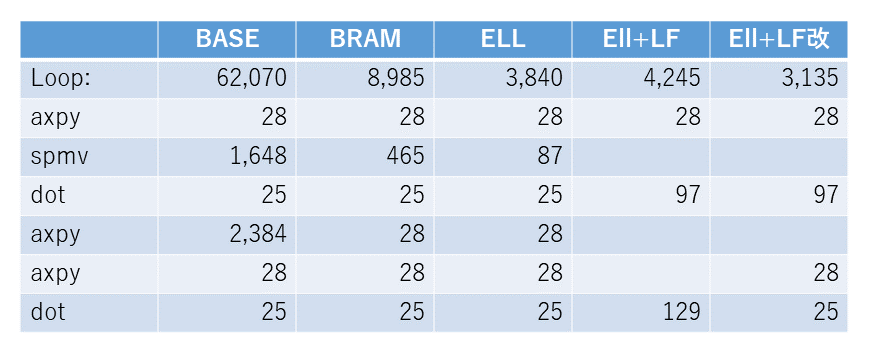
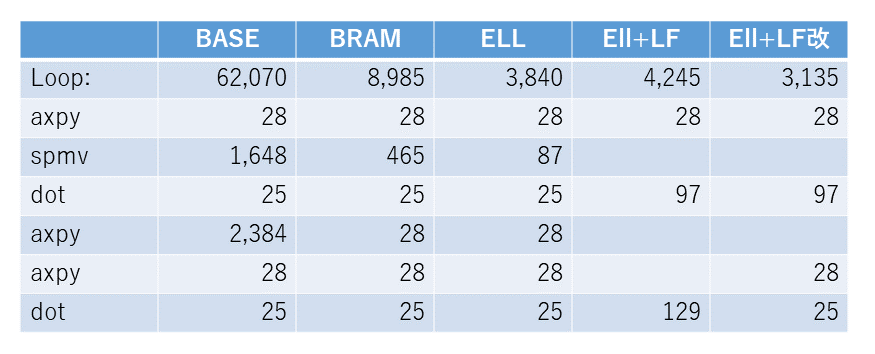
CG 法のカーネルを最適化して高速化してみます。先に表1に結果を示しておきますが、62,070サイクルかかっていたのが、最終的には3,135サイクル、約1/20に高速化されました。この過程を順に説明していきます。今回のブログの冒頭でも説明しましたが、github 上の solver/cg_ocl_base ディレクトリの元のプログラムに高速化手法を適用することで、最終的には solver/cg/ocl_ell_lf2 ディレクトリのプログラムが得られます。
BRAM の活用
CG 法では解が収束するまで axpy, spmv, dot などの処理が繰り返されます。これらの処理にかかる時間 (Latency) の見積もりがクロックサイクル数や実時間を単位として得られます。表1の BASE の列は、前回から使っている CG 法のカーネルの各ループの遅延 (単位はクロックサイクル) になります。
このうち、spmv はループの繰り返し回数がデータによって異なるため正確な遅延が得られませんが、以下のような情報は得られます。
- 外側ループの繰り返し回数 (Trip Count) 16回
- 内側ループの1反復の遅延 (Iteration Latency (cycle)) 86サイクル
- 内側ループの反復の投入間隔 (Interval) 6サイクル
また、内側ループの反復回数は今回使った例では最大5回、平均4回程度になります。これらのパラメータを使い、内側ループがパイプライン化されていることを考慮して、spmv の遅延は以下のように見積もりました。
BASE の spmv の遅延: (6 x 4 + (86-6-1)) x 16 = 1,648
これらのループの遅延を合計すると4,138サイクル程度になります。
今回使用しているデータでは、最初の1回目の反復で初期解を求め、解が収束するまで2-16回目の15回同じ処理が繰り返されます。後者の15回の反復は、合計で62,070 (=4,138 x 15) サイクル程度と見積もることができます。
では、各ループの遅延情報からボトルネックとなる箇所を探してみましょう。axpy が3回呼び出されていますが、1回目と3回目が28サイクル
で終了しているのに対し、2回目のみ2,384サイクルもかかっています。
axpy(beta, p, r, p);
axpy(alpha, p, x, x);
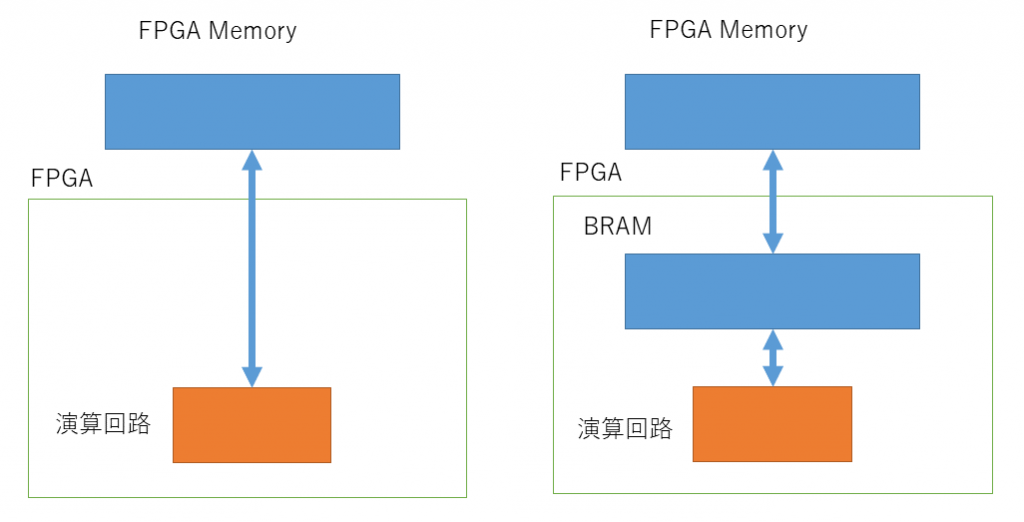
axpy(-alpha, q, r, r);3つの axpy の実引数は上記のようになります。2回目の axpy で参照している配列 x のみがカーネル終了後にカーネルからホストへ転送されるデータで、それ以外の配列 p, q, r はカーネル内で宣言されている一時変数です。配列 x が (FPGA から直接アクセス可能ですが) FPGA 外に接続されているメモリに配置されていることが原因と思われます。このメモリをここでは FPGA メモリと呼ぶことにします。
前回ホストからカーネルへのカーネルトップ関数の引数のデータ転送について説明しました。カーネルトップ関数の配列の引数は、FPGA から直接アクセスできる FPGA メモリ内に領域が確保されます。FPGA から直接アクセスできるといっても、そのメモリへのアクセス時間が非常に長いことが予想されます。
これに対してカーネルで宣言された p, q, r といった配列は、FPGA 内で高速にアクセスできる BRAM 上に確保されます。
図の左側に示すように、spmv の演算回路では FPGA メモリ上の配列 x を直接アクセスしていると思われます。そこで、図7の右側に示すように、FPGA 内の BRAM 上にバッファを用意し、spmv の演算回路からは BRAM 上のバッファにアクセスして高速化を試みます。
具体的には、以下のようにコードを書き換えます。前回、カーネルトップ関数として kernel_func という関数を用意して、その関数から solve という C++ の template 関数を呼ぶようにカーネルを修正しました。この kernel_func 関数内で、solve 関数を呼び出す前後に、カーネルトップ関数の配列の引数をFPGA メモリと BRAM との間でコピーするようにしましょう。
- ホストからカーネルへの入力となる配列 colptr, col, val をメモリから BRAM へコピーします。
- solve 関数を呼び出します。
- カーネルからホストへの出力となる配列 x を BRAM からメモリへコピーします。
BRAM には、これらの配列に対応する kernel_colptr, kernel_col, kernel_val, kernel_x といったバッファとなる配列を確保します。これらの配列のサイズが大きくなりすぎると FPGA 内の BRAM に収まりきらなくなりますが、その対処法は次回以降に説明することとします。
さらに、この後 CG 法のプログラムへの最適化を試みますが、その効果がわかりやすいように、solve 関数の CG 法の1回目の反復と2回目以降の反復を分けて記述し、反復回数を15回に固定します。この2回目以降の15回の反復を、このブログではカーネルループと呼ぶことにします。
修正後のカーネルループとその内側の各ループの遅延を Emulation-HW で見積もったのが表1の BRAM の列です。spmv は BASE と同様に手計算で見積もっています。
表1を見ると、2回目の axpy の遅延が大きく減少していることが確認できます。また、spmv も疎行列のデータはホストから FPGA メモリへコピーした配列でしたので大きな遅延が発生していたようですが、修正後は同様に遅延が小さくなっていることが確認できます。
疎行列のデータ構造の CRS 形式から ELL 形式への変更
axpy の遅延が小さくなると、今度は、spmv の遅延の大きさが気になります。FPGA 向けの spmv の最適化手法としては参考文献 [1] をはじめとして様々な研究が行われていますが、それらは比較的大規模な行列を対象としているようです。今回は、小規模な行列でも最適化の効果が確認できそうな、疎行列のデータ構造の変更を試みます。
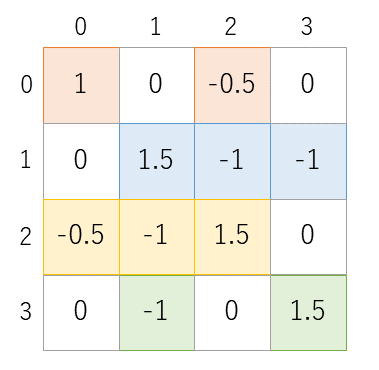
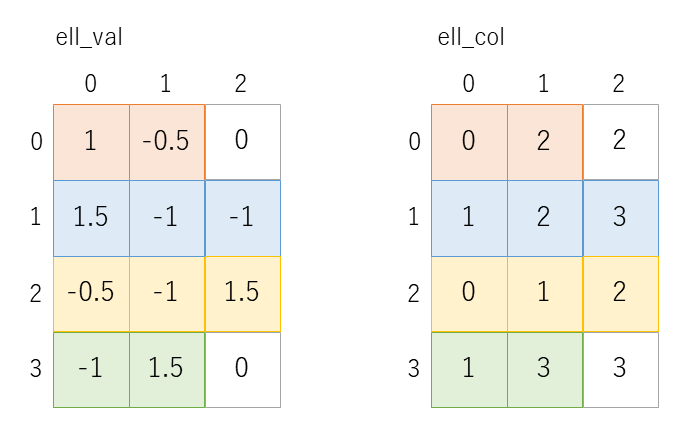
サンプルとして用いている連立一次方程式の係数行列は16×16ですが、
その左上の4×4のみを抜き出したものを図8に示します。
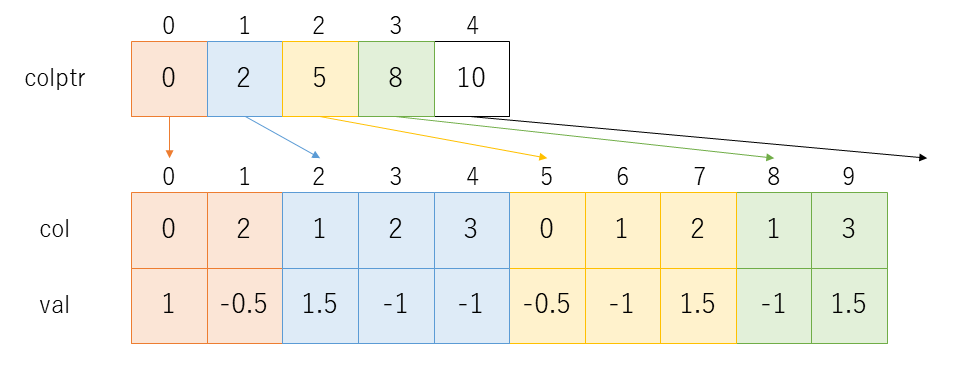
この行列の値が0ではない要素、つまり非零要素のみを取り出して行列のサイズを圧縮するデータ構造には様々なものがあります。CG 法のプログラムでは図9に示すような CRS(Compressed Row Storage) と呼ばれるデータ構造を使っています。
0, 1, 2, 3行目の非零要素にはそれぞれ薄い赤、青、黄、緑の色をつけています。配列 val は各行の非零要素の値のみを取り出して1次元配列上にならべたものです。配列 col はそれらの非零要素が元の行列の何列目 (横方向に何番目か)を表したものになっています。これだけでは非零要素が何行目 (縦方向に何番目か)のものかがわかりませんので、配列 colptr を使って、0,1,2,3 行目の非零要素が配列 val, col の何要素目から始まる領域に格納されているかを示すようになっています。
i行目の非零要素は、配列val, col の colptr[i] 番目から colptr[i+1]-1 番目までの領域に格納されます。ただし、最終行のみ、工夫が必要になります。4×4の例では colptr[4] を用意することで、3行目の非零要素が colptr[3] の 8番目から colptr[4]-1 の 9番目に格納されていることがわかるようにしています。
このように CRS などのデータ構造を用いることで、非零要素のみのメモリ領域が確保され、使用メモリ量が削減されます。また、メモリアクセス回数も減少し、処理の高速化につながります。大規模な疎行列は値が0の要素が大半を占め、非零要素の割合は非常に小さいことが多いため、メモリ量の削減とメモリアクセス回数の減少による高速化の効果が大きくなります。ただし、それらの効果と引き換えに以下の spmv の疎行列とベクトルの積のコードのように処理がやや複雑になります。
for (i=0; i<N; i++) {
cb = colptr[i];
ce = colptr[i+1];
ret[i] = (T)0;
for (j=cb; j<ce; j++) {
ret[i] += val[j] * b[col[j]];
}
}疎行列のデータ構造としては、ELL (Ellpack/Itpack) なども使われることが
多いようです。これも4×4の例を図10に示します。
各行の非零要素数の最大値 NZ を使い、非零要素の値は N×NZ の2次元配列 ell_val に格納されます。非零要素の列番号も同様に N×NZ の配列 ell_col に格納されます。非零要素数が NZ より少ない行は、ell_val では0を埋め、ell_col では最後の非零要素の列番号などを埋めておきます。このようにすると、疎行列とベクトルの積は、以下に示すように N×NZ 回の定数回の繰り返しの2重ループとして記述されます。FPGA では、このように定数回のループに変換することで高速化を図ることができます。
for (i=0; i<N; i++) {
ret[i] = (T)0;
for (j=0; j<NZ; j++) {
ret[i] += ell_val[i][j] * b[ell_col[i][j]];
}
}ELL 形式を用いた spmv では、0で穴埋めされた値を使ったダミーの計算が行われることに注意して下さい。このダミーの計算の増大とループの繰り返し回数を定数回にしたことによる高速化とはトレードオフの関係になります。各行の非零要素数のばらつきが小さいと、どの行の非零要素数も NZ に近い値となり、0で穴埋めされた値を使ったダミーの計算が少なくなり、ELL に適していると言えますが、逆に非零要素数のばらつきが大きいと、ダミーの計算が増大してしまい、高速化につながらないこともあります。
さて、CG 法のプログラムについても、ホストプログラムで係数の疎行列を CRS 形式から ELL 形式に変換し、カーネルでは ELL 形式に対応した spmv_ell という疎行列ベクトル積を実行するようにしてみましょう。Emulation-HW でループの遅延を見積もった結果が、表1 の ELL の列になります。spmv の遅延が465サイクルから87サイクルへと大きく減少したことが確認できました。
ループ融合
さらにカーネルを高速化することを考えてみます。
コードをよく見ると、spmv で得られたベクトル q が続く dot で使われていたり、2つの axpy が続き、その axpy で得られたベクトル r が dot で使われていたりすることがわかります。そこで、これらのループをまとめてみます。この手法はループ融合などと呼ばれることもあります。2つの axpy とそれに続く dot のループ融合例は以下のようになります。
T sum = (T)0;
for (int i=1; i<N; i++) {
x[i] = x[i] + alpha * p[i];
r[i] = r[i] - alpha * q[i];
sum += r[i] * r[i];
}
return sum;Emulation-HW で遅延を見積もった結果が表1の ELL+LF の列になります。表1がこのブログのかなり上の方になってしまいましたので、表2としてこの表をセクションの最後に再掲しておきます。spmv と dot のループ融合の遅延を dot の行に、2つの axpy と dot のループ融合の遅延は2つ目の dot の行にそれぞれ示しています。spmv と dot のループ融合の結果は効果はあったのですが、2回目と3回目の axpy と最後の dot のループ融合は、逆に遅延が大きくなってしまいました。
そこで、2回目と3回目の axpy のみループを融合し、dot は融合しないことにしてみます。その見積もり結果が表2の ELL+LF改 の列になります。
以上まとめると、16×16の疎行列の係数行列を持つ連立一次方程式を解くプログラムのカーネルループについて、以下のような高速化を行ったことになります。
- FPGA メモリ上のデータのバッファを FPGA 内の BRAM に確保しました。
- 疎行列のデータ構造を CRS 形式から ELL 形式に変更しました。
- ループ融合を適用しました。
高速化の結果、62,070サイクルから3,135サイクルまで約1/20に高速化できました。繰り返しになりますが 高速化前と後のプログラムはそれぞれ github 上の solver/cg_ocl_base ディレクトリと solver/cg/ocl_ell_lf2 ディレクトリに置いてありますので参考にして下さい。
まとめ
今回は CG 法のプログラムの FPGA 上でのカーネルの実行の高速化を試みました。今回は使った係数行列は16×16という小規模なものですので、さらにサイズの大きい問題への対処が課題として挙げられます。これについては次々回に解説したいと思います。その前に、次回は Alveo U50 だけでなく、ZC706 や Ultra96V2 などのテストボードでの CG 法のプログラムの実行法を説明したいと思います。
参考文献
[1] A. Kumar et.al: A Domain-Specific Architecture for Accelerating Sparse Matrix Vector Multiplication on FPGAs, in Proc. FPL 2020, pp.127-132.
広島市立大学 窪田昌史