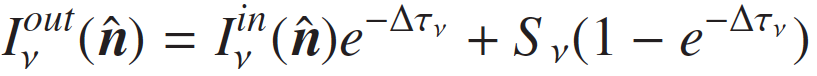どうも皆さんお久しぶりです。筑波大学計算科学研究センター所属の小林諒平です。
昨年はスーパーコンピュータでも使われ始めた FPGA という記事を執筆させて頂き、そして今年また本ブログにて記事を執筆させて頂く機会を賜りましたので、今回は計算科学研究センター (以下、当センター) にて FPGA をどのように活用しているのかについて紹介していきたいと思います。
このコースは、ACRiQ1.04 と同じように FPGA やアダプティブコンピューティングの研究論文をその著者が紹介するシリーズで、その第二弾となります。タイトルの通りで恐縮ですが、このコースでは宇宙物理アプリケーションを題材にしており、それを複数の FPGA を活用し、高速化に成功したという研究成果について紹介します。
こちらの研究成果は、昨年の11月に開催された高性能計算技術の世界最高峰の国際会議 SC20 の併設ワークショップ H2RC (Sixth International Workshop on Heterogeneous High-performance Reconfigurable Computing) にて発表され、その論文も公開されていますので、興味のある方はその論文と併せて本記事をお読み頂くと理解が深まると思います。
それでは、本コースの第一回目は、対象としている宇宙物理アプリケーションについて紹介し、それに対して何故 FPGA の利用が有効であると当センターは睨んでいるのかについて説明します。
宇宙輻射輸送シミュレーションコード Accelerated Radiative transfer on Grids using Oct-Tree (ARGOT)
当センターでは、複数の物理モデルや複数の同時発生する物理現象を含むシミュレーションであるマルチフィジックスアプリケーションを加速させるために、GPU と FPGA を適材適所的に併用することが重要であると考えています。
なぜなら、マルチフィジックスアプリケーションは、その特性上、シミュレーション内に様々な特性の演算が出現するため、GPU だけでは演算加速が困難な場合があります。そのため、GPU だけでは対応しきれない特性の演算の加速に FPGA を利用することで,アプリケーション全体の性能向上を狙うというのが当センターの掲げているコンセプトです。
本コースで紹介する研究成果は、宇宙輻射輸送シミュレーションコード Accelerated Radiative transfer on Grids using Oct-Tree (ARGOT) というマルチフィジックスアプリケーションを対象にしています。ARGOT コードは、宇宙輻射輸送方程式 (輻射輸送⽅程式:光のエネルギー輸送について記述された⽅程式) を解くことを目的とした、当センターで開発されているプログラムです。これを用いることで、初期宇宙における天体形成をシミュレーションします。
こちらの記事でも紹介されている通り、ARGOT コードの最大の特徴は「点光源からの輻射輸送を計算する ARGOT 法」と「空間に広がる光源からの輻射輸送を計算する Authentic Radiative Transfer (ART) 法」との2つのアルゴリズムを組み合わせて輻射輸送方程式を解く点です。そして、ART 法がこのアプリケーション全体において支配的な演算となっているため、ART 法を如何に演算加速させるかがアプリケーション全体の性能向上に直結します。
支配的な演算処理 ART 法
ART 法は一種のレイトレーシングに基づくアルゴリズムです。
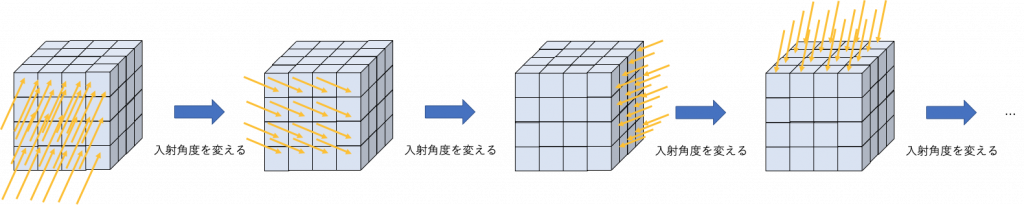
下の図のように、3次元の問題空間をメッシュに分割し、境界面から複数のレイ (平行光) を発射し輻射輸送を計算します。ART 法におけるレイの前提条件として、レイの反射や屈折は起こらず、レイの方向 (入射角度) は HEALPix ライブラリで求められます。
そして、これらのレイがメッシュを通過する度に以下の式が計算されます。この式が ART 法の演算カーネルで、式における ν、Iνin、Iνout、nˆ、 ∆τ、Sν はそれぞれ振動数、入力放射強度、出力放射強度、レイの方向、メッシュにおける光学的厚み、メッシュの source function を表します (これらの用語の解説は割愛します)。なお、ART 法の計算は全て単精度浮動小数点数を用いて行われます。
ART 法がどのくらいの規模感の計算であるかを説明していきます。メッシュの1辺の長さを N とすると、レイが1本の場合の計算量は直線的に進むレイが通過するメッシュの個数に相当するので、O(N) となります。その肝心のレイの本数ですが、レイは境界面から入射する平行光であるため、その本数は N2 となります (面から入射するので) 。すなわち、ART 法のある入射角度における計算量は O(N3) となります。そして、ART 法では少なくとも768方向 (上述した HEALPix ライブラリで求める) のレイを扱うため、レイの総数は 768 × N2 となります。この入射角度の総数を Nang とすると、ART 法の計算量は O(NangN3) となるため、ART 法の高速化には莫大な計算能力を持つハードウェアが必要であることが分かると思います。
ART 法はレイトレーシングを用いているため、ある1つのレイに関する計算は進路に応じて順序通りに計算しなければなりませんが、異なるレイの間には計算の依存関係がなく並列に計算できます。このことから、莫大な計算能力を持つ CPU や GPU を使って並列コンピューティングすればいいじゃないという話になるのですが、ART 法は CPU や GPU のような SIMD-like なアーキテクチャの計算デバイスにとって厄介な点が2つあります。その2つの点について、説明していきます。
ART 法のここが厄介!
1つ目の厄介な点は、メッシュデータに対するメモリアクセスパターンがレイの方向によって様々 (数百から数千パターン) になるため、複数のレイの計算を SIMD で計算する際に、メッシュデータがメモリ上で連続しない場合が起こり得ることです。このため、キャッシュヒット率の低下や GPU においてメモリアクセスレイテンシの大きさが問題になる可能性があります。
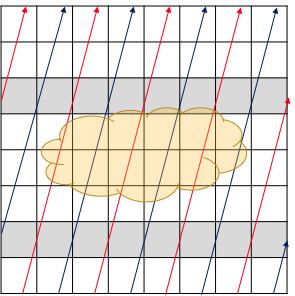
そして、2つ目の厄介な点はメッシュに対する積分計算が衝突する可能性があることです。下の図 (説明のしやすさのために2次元の図にしています) のように、ART 法では、同じメッシュを隣接した複数のレイが通過する (図の灰色でマークされている領域) 可能性があるため、メッシュ上の複数のレイの効果を重ね合わせる必要があります。
このためによく使われるのが、atomic 演算ですが、atomic 演算にはそこそこのオーバーヘッドがあるので、出来ることなら atomic 演算を回避したいのが本音です (必要となる atomic 演算の回数のオーダーは N3 です) 。そのための手段としては、図に示すように、赤色と青色のレイのように隣接するレイを同時に計算しないというのがあります。しかし、この場合だとメモリアクセスパターンがより飛び飛びになり、ただでさえメモリアクセスで問題を抱えているアルゴリズムなのにその問題を更に悪化させてしまうというデメリットがあります。
こうしたART 法の性質から、SMID-like な計算デバイスにとって ART 法は不向きな演算であると言わざるを得ないと当センターでは判断しています。
一方、FPGA はオンチップの内蔵メモリを持ち、低レイテンシ・高バンド幅にランダムアクセスが可能です。それに加えて、FPGA であれば ART 法に最適化したメモリアクセス回路をハードウェアに組み込むことが可能です。このことから、当センターは、ART 法は FPGA での実装に適したアルゴリズムである可能性が高いと見込み、FPGA を活用した ART 法の演算加速についての研究に着手しました。
補足事項
ART 法がレイトレーシングに基づくアルゴリズムなら、NVIDIA Turing アーキテクチャに上手くハマるのではないか、と考えられると思います。しかし残念ながら、NVIDIA Turing アーキテクチャが対象とするレイトレーシングと ART 法のレイトレーシングは本質的に異なる計算です。
前者は主に CG におけるレイトレーシングであり、物体表面での光の反射や透過を観測者の視点方向からさかのぼって計算するもの (主な演算はレイとオブジェクトの交差判定) です。一方、後者におけるレイトレーシングは、様々な方向の光線を解いて計算領域内の各点での平均輻射強度を計算するものであり、交差判定のような演算は含まれていません。
したがって、両者の間では「レイトレーシング」という言葉が共通しているだけであり、仮に ART 法を Turing アーキテクチャの NVIDIA GPU で実行させても、Turing アーキテクチャならではの恩恵を受けることはできないでしょう。
まとめ
本コースの1回目では、当センターが、どのようなアプリケーションに対して、どのような観点で FPGA を利用するかについて紹介しました。次回は、ART 法を加速する演算コアをどのように FPGA に実装していくかを紹介していきます。どうぞお楽しみに。
筑波大学 計算科学研究センター 小林諒平