この記事では、私たちが国際会議 FCCM 2017 (論文 [1]) で提案したソーティングを高速化するための基本的なアイデアを解説していきます。提案したアイデアのベースラインは、2014年の国際会議 FPGA でスタンフォード大学の Casper と Olukotun によって発表された方式 (論文 [2]) です。
前回の記事で説明したように、これまで提案された FPGA ソーティングアクセラレータの基本的な構成要素は、2つのソートされた系列を1つの系列にマージするマージロジック回路です。一般に、マージロジック回路の性能が N 倍に向上すると、ソーティング性能は N 倍に高速化されます。そのため、マージロジック回路の性能の向上は非常に重要であり、FPGA ソーティングアクセラレータ研究の1つの主題と見なされています。私たちの FCCM 2017 論文の着目点もこれです.
ベースラインのマージロジック回路
マージロジック回路の基本的な概念は2011年の国際会議 FPGA で Koch と Torresen によって紹介されました (論文 [3]) 。次の図はこの動作例を示します。
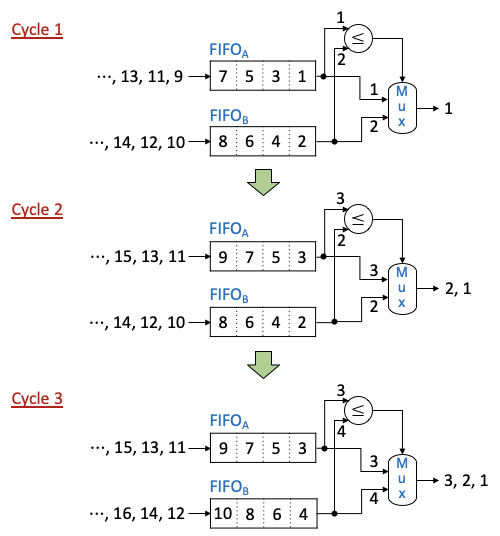
この例では、1, 3, 5, 7, 9, … というソートされた奇数の系列と、2, 4, 6, 8, 10, … というソートされた偶数の系列をマージして、1つのソートされた系列 1, 2, 3, 4, 5, 6, … を作ります。入力系列は FIFOA と FIFOB という2つの First In First Out バッファに格納されています。各クロックサイクルに、FIFOA と FIFOB の先頭レコード (つまり、それぞれのバッファに格納されているレコードの中の最小レコード) が比較され、小さい方がマルチプレクサ Mux により出力されます。サイクル1では、FIFOA の最小レコード1が FIFOB の最小レコード2より小さいため、1が FIFOA から取り出されて、Mux により出力されます。サイクル2では、FIFOB の最小レコード2は FIFOA の最小レコード3より小さいため、2が出力されます。このように、最終的に 1, 2, 3, 4, 5, 6, … というソートされた1つの系列が得られます。
Koch と Torresen のマージロジック回路は各クロックサイクルに1個のレコードしか出力できません。
ソーティング性能を向上するために、Casper と Olukotun は各クロックサイクルに複数のレコードを出力できるマージロジック回路を提案しました。このブログでは、各クロックサイクルに E 個のレコードを出力できるマージロジック回路を E レコードのマージロジック回路と呼ぶことにします。次の図は、Casper と Olukotun の 4 レコードのマージロジック回路とその動作例を示します。
Koch と Torresen のマージロジック回路のように、入力系列は FIFO バッファに格納されます。図中に黄色で示した4個のフィードバックレジスタ (Feedback registers) は最小のレコードで初期化されます。この例では、0を最小のレコードとするので、4個のフィードバックレジスタを0で初期化します。各クロックサイクルでは、2つの FIFO のうち、先頭(最小)のレコードが小さい方を選択し、選択された FIFO から4個のレコードを読み出します。これらのレコードとフィードバックレジスタに格納されているレコード、合計8個のレコードはマージャ (Merger) に入力されます。マージャは8個の入力レコードをソートして、小さい4個のレコードを出力、大きい4個のレコードをフィードバックレジスタに保存します。
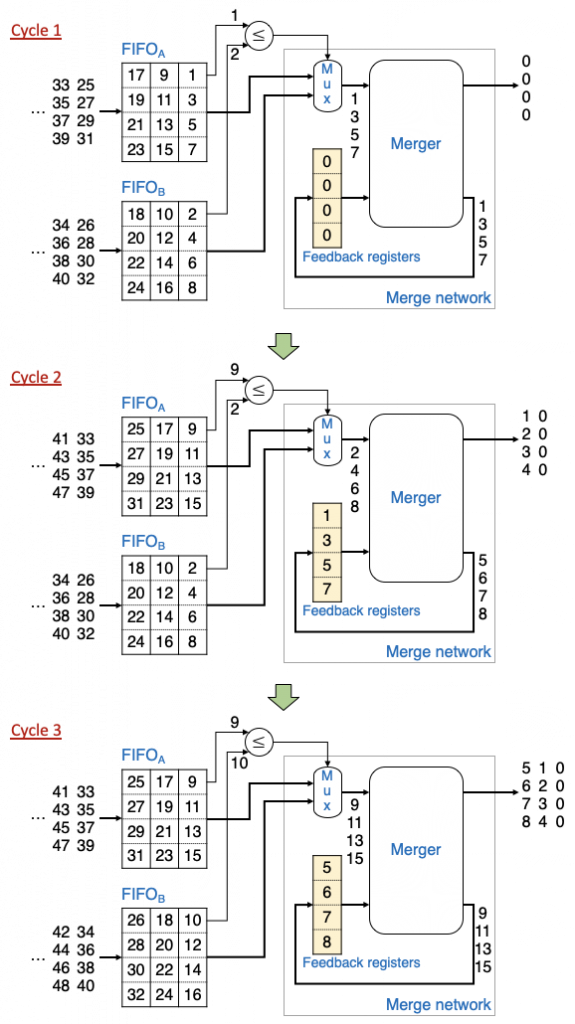
以下に具体的な動作例を説明します。この例の入力系列は図1と同じです。
サイクル1では、FIFOA と FIFOB の最小レコードはそれぞれ1と2です。1は2より小さいため、 FIFOA から4個のレコード (1, 3, 5, 7) が読み出されます。これらのレコードとフィードバックレジスタに格納されているレコード (0, 0, 0, 0) がマージャでソートされて (0, 0, 0, 0, 1, 3, 5, 7) を得ます。この中の小さい4個のレコード (0, 0, 0, 0) が出力、大きい4個のレコード (1, 3, 5, 7) がフィードバックレジスタに保存されます。ただし、このサイクルの出力レコード (0, 0, 0, 0) は2つの入力系列のレコードではなく初期状態にフィードバックレジスタに入るものなので出力系列から除外されます。
サイクル2では、FIFOA と FIFOB の最小レコードはそれぞれ9と2です。2は9より小さいため、 FIFOB から4個のレコード (2, 4, 6, 8) が読み出されます。これらのレコードとサイクル1にフィードバックレジスタに保存された4個のレコード (1, 3, 5, 7) がマージャでソートされて (1, 2, 3, 4, 5, 6, 7, 8) を得ます。この中の小さい4個のレコード (1, 2, 3, 4) が出力、大きい4個のレコード (5, 6, 7, 8) がフィードバックレジスタに保存されます。
同様に、サイクル3では、マージャは FIFOA からの4個のレコード (9, 11, 13, 15) とフィードバックレジスタに格納されている4個のレコード (5, 6, 7, 8) をソートし、小さい4個のレコード (5, 6, 7, 8) を出力、大きい4個のレコード (9, 11, 13, 15) をフィードバックレジスタに書き戻します。
このように、2つの入力系列がクロックサイクルあたり4個の出力レコードのスループットで正しくマージされます。
上記の説明でマージャをブラックボックスとして扱っていました。1つのクロックサイクルで、ソートされた2つの短い (図2では4個のレコードの) 系列をソートされた1つの系列にマージする組み合わせ回路であることを説明しました。実際にはいくつかの実装方法があります。次図はその中の1つバイトニック・マージャ (bitonic merger) を示します。
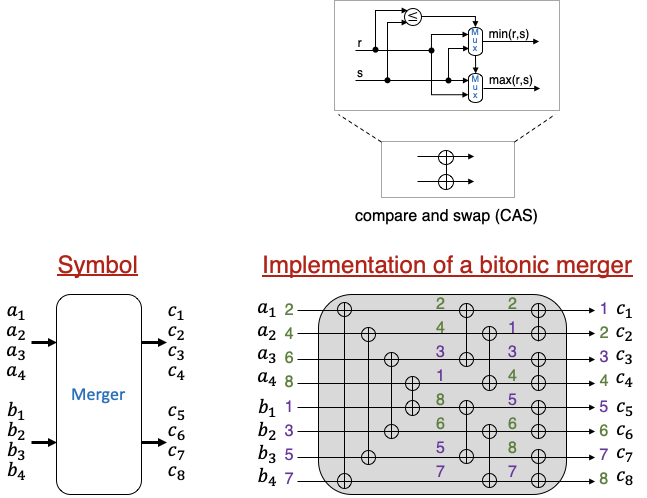
バイトニック・マージャはバイトニック・ソーティングネットワークの一部分であり、50年以上前に Batcher (アメリカの計算機科学者) によって開発されました (論文 [4]) 。このマージャは複数の compare and swap (CAS) ユニットから構成されます。各 CAS ユニットは2つの入力レコードを持ち、上部の入力レコードが下部の入力レコードより大きい場合、それらのレコードを入れ替えます。
例えば、図3の動作例では、左端の CAS ユニットの入力は2と7です。上部の入力2は7より大きくないので入れ替えは起きずに出力されます。また、別の左から4個目の CAS ユニットの入力は8と1です。8は1より大きいため、それらの値が入れ替わり上部の出力が1で下部の出力が8となります。
CAS ユニットの数は入力系列の長さにより決められます。図3のバイトニック・マージャ (2つの入力系列の長さ = 4) は12個の CAS ユニットから構成されます。一般に、長さ E の2つの入力系列をマージするバイトニック・マージャを作るために、 E+E*log2E 個の CAS ユニットが必要となります。
ベースラインのマージロジック回路の問題点
ベースラインのマージロジック回路 (図3) の問題点を理解するために、まず、回路のクリティカルパス (critical path) について簡単に説明します。
クリティカルパスは、全体の回路で最も長い (つまり、最大遅延を持つ) パスです。ここで、パスとは、状態要素 (例えば、フリップフロップ) から状態要素へ、入力から状態要素へ、状態要素から出力へ、または入力から出力への一連のゲートを通過する経路です。例えば、下図の回路のクリティカルパスは a から y までのパス、または b から y までのパスです。どちらの長さも3段の AND ゲートです。
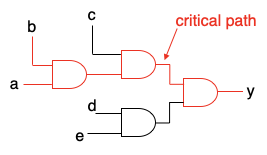
クリティカルパスの遅延が回路の最大動作周波数 (つまり、性能) を決定します。具体的には、短いクリティカルパスを持つ回路は高いクロック周波数で動作します。逆に、長いクリティカルパスを持つ回路は低いクロック周波数でしか動作しません。そのため、回路設計では、クリティカルパスを短縮する (ゲート段数を削減する) ことが非常に重要です。
次に、ベースラインのマージロジック回路の問題点を説明します。マージスループットは1サイクルあたりの出力レコード数 (E) だけでなく、回路の動作周波数 (F) にも比例します。しかし、ベースラインのマージロジック回路では、E を増やすと、クリティカルパスのゲート段数が増加するため F が大幅に低下します。
ベースラインのマージロジック回路のクリティカルパスはマージャを通るパスです。次の図はそのようなパスをハイライトしています。
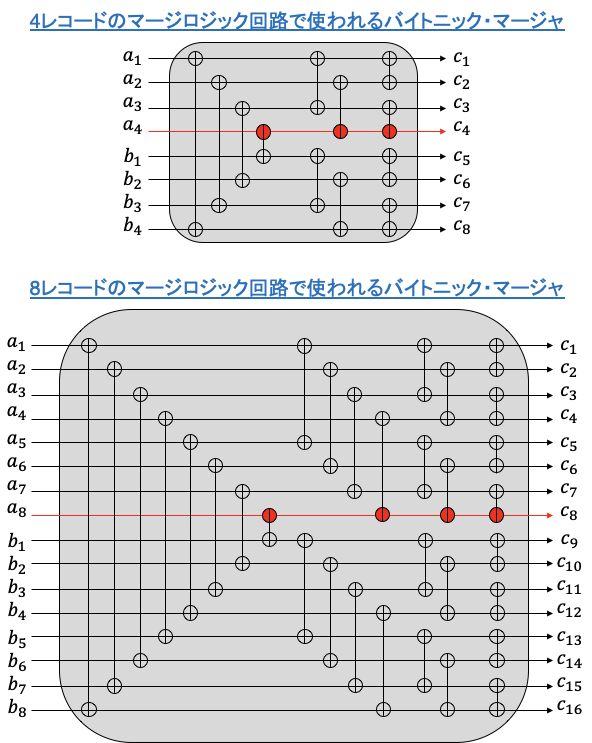
図に示すように、4レコードと8レコードのマージロジック回路で使われるバイトニック・マージャのクリティカルパスはそれぞれ3段と4段の CAS ユニットです。一般に、Eレコードのマージロジック回路で使われるバイトニック・マージャのクリティカルパスの CAS 段数は 1+log2E となります。このように、Eが増えると、クリティカルパスのゲート段数が増加します。マージャは1サイクルで処理しないと正しく回路が動作しないため、パイプライン処理などで単純にクリティカルパスのゲート段数を削減することは困難です。
提案したマージロジック回路の基本的なアイデア
次の図は提案したマージロジック回路を実現するためのカギとなるアイデアを示します。
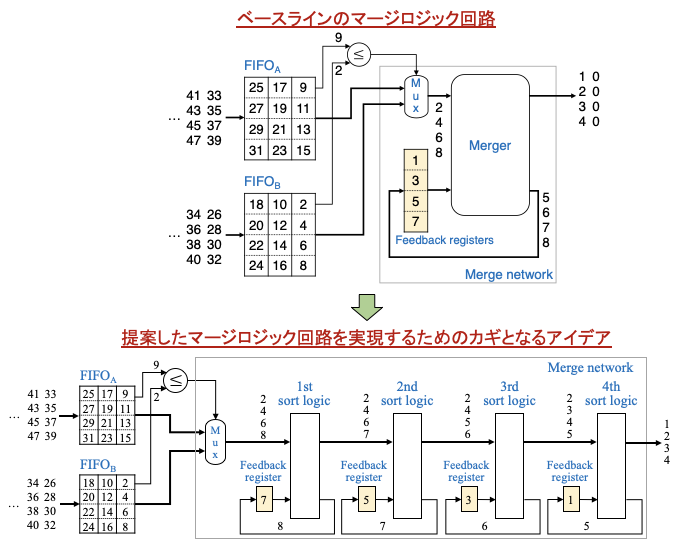
この動作例は図3の動作例の cycle 2 と同じです。ベースラインのマージロジック回路の大きなマージャを複数の小さなソートロジック (sort logic) と呼ぶ回路に分割します。ソートロジックの数はフィードバックレジスタの数と同じです。各ソートロジックは自分自身の入力をソートし、最大のレコードを対応のフィードバックレジスタに書き戻します。
例えば、1番目 (左端) のソートロジックは FIFOB からの4個のレコード (2, 4, 6, 8) とフィードバックレジスタに格納されているレコード (7) をソートして (2, 4, 6, 7, 8) を得ます。その中の小さい4個のレコード (2, 4, 6, 7) を2番目のソートロジックに出力、最大のレコード (8) をフィードバックレジスタに書き戻します。同様に、2番目のソートロジックは4個のレコード (2, 4, 5, 6) を3番目のソートロジックに出力、1個のレコード (7) をフィードバックします。このように、最終的に4個のレコード (1, 2, 3, 4) が出力されます。これは、ベースラインのマージロジック回路の出力と同じです。
詳しくは次回に解説しますが、次に、ソートロジックの処理をパイプライン化することで、マージロジック回路全体のクリティカルパスを1個のコンパレータと1個の2入力マルチプレクサだけに削減できます。そうすると、1サイクルあたりの出力レコード数 (E) を増やしてもクリティカルパスは一定で変わらなくなります。すなわち、先に青色で強調して示した問題点を解決することになります。
まとめ
今回は私たちがベースラインとして用いたマージロジック回路と基本的なアイデアを説明しました。特に回路のクリティカルパスを短縮することが重要になることに注意してください。
次回は、提案マージロジック回路のアーキテクチャ、動作例、特徴を解説していきます。
東工大 Thiem Van Chu
参考文献
- Susumu Mashimo, Thiem Van Chu, and Kenji Kise, “High-Performance Hardware Merge Sorter,” The 25th IEEE International Symposium On Field-Programmable Custom Computing Machines (FCCM), May 2017.
- Jared Casper and Kunle Olukotun, “Hardware Acceleration of Database Operations,” The 22nd ACM/SIGDA International Symposium on Field-Programmable Gate Arrays (FPGA), Feb. 2014.
- Dirk Koch and Jim Torresen, “FPGASort: A High Performance Sorting Architecture Exploiting Run-time Reconfiguration on FPGAs for Large Problem Sorting,” The 19th ACM/SIGDA International Symposium on Field-Programmable Gate Arrays (FPGA), Feb. 2011.
- Ken Batcher, “Sorting Networks and Their Applications,” The Spring Joint Computer Conference, Apr. 1968.

