みなさんこんにちは。このコースでは FPGA を使いこなすために理解しておきたい論理回路の基礎について 5 回にわたって説明します。RTL (Register Transfer Level) で FPGA 開発をするための入門になります。また,高位合成で開発をしていても、FPGA の性能を引き出すためには自分で記述するコードがどのようなハードウェアになるかを理解するための知識です。電気・情報系の大学の 2 年生くらいで学ぶ内容ですが、ハードウェアはよく分からないという方はぜひお付き合いください。
1 回目は論理代数の基本的な説明です。論理演算とそれに対応する論理回路を説明します。まだ 4 ビットカウンタは登場しません。
論理代数の基礎
論理回路は値が 0 と 1 のみの世界で入力情報に対して計算・判断・記憶を行い結果を出力します。論理演算が、この計算にあたります。FPGA からは一旦離れ、論理回路にからめて論理代数を説明します。最後に FPGA ではどうなっているかという話をします。
変数の値はすべて 0 か 1
論理代数では、すべての変数は 0 か 1 の値をとります。つまり、変数 \(x\) があったら、その値は 0 か 1 のどちらかです。
一般的な論理回路では、0 と 1 を電圧が 0 ボルト (Low) と高い状態 (High) に対応させます。実際の回路では、高い状態が何ボルトかは設計によります。0 も完全に 0 ボルトにはなりません。また、Low でも High でもない状態も存在します。しかし、ひとまず 0 といったら 0 ボルト、1 といったら電圧が高いと思ってください。
基本的な論理演算
私たちが普通に扱っている 10 進数の世界で四則演算があるように、0 と 1 の世界でも演算が定義されています。その基本的な演算が否定 (NOT)、論理積 (AND)、論理和 (OR)です。論理回路で論理演算を実現する素子は論理ゲートと呼ばれ、それぞれ NOT ゲート、AND ゲート、OR ゲートと呼ばれます。
NOT 演算
NOT 演算は変数の値を逆転します。演算子は「  ̄ 」です。例えば、変数 \( X \) が 0 のとき、\(Z = \overline{X}\) は 1 です。左のカラムを入力、右のカラムを出力として、入力と出力の 0、1 の組み合わせを列挙すると次の表になります。
| \(X\) | \(Z\) |
|---|---|
| 0 | 1 |
| 1 | 0 |
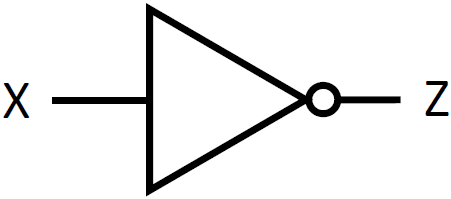
論理回路では NOT ゲートと呼ばれ、回路図では下の図の記号を使います。
AND 演算
AND 演算は、2 つの変数がどちらも 1 の場合にだけ 1 となる演算です。演算子は「 \(\cdot\) 」を用いて \(X \cdot Y\) のように表記しますが、演算子を省略して単に \(XY\) とも表記します。論理積という名前の通り、0 と 1 の組み合わせのかけ算になっています。下の表のように 2 つの変数の取り得る値の組み合わせは 4 通りあり、入力 \(X\) と \(Y\) がともに 1 の場合だけ \(Z = X \cdot Y\) は 1 になります。
| \(X\) | \(Y\) | \(Z\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
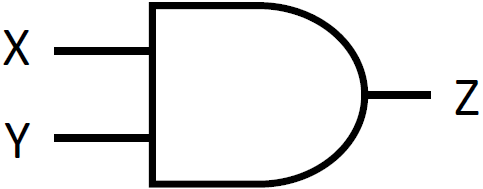
論理回路では AND ゲートとも呼ばれ、回路図では下の図の記号を使います。
OR 演算
OR 演算は、2 つの変数の少なくとも 1 つが 1 の場合に 1 となる演算です。演算子は「\(\lor\)」を用いて \(X \lor Y\) のように表記します。論理和という名前で 0 と 1 の組み合わせの足し算になっているのですが、両方とも 1 のときは 1 のままという演算です。下の表のように2つの変数の取り得る値の組み合わせは 4 通りあり、入力 \(X\) と \(Y\) がともに 0 の場合だけ \(Z = X \lor Y\) は 0、ほかは 1 になります。
| \(X\) | \(Y\) | \(Z\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
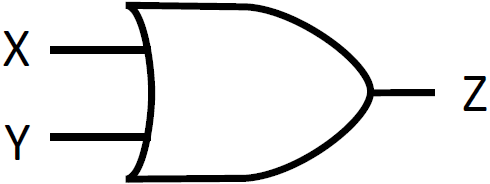
論理回路では OR ゲートとも呼ばれ、回路図では下の図の記号を使います。
この 3 つの演算が基本となり、交換則や結合則などの論理代数の定理が成り立ちますが、これについては、この記事では割愛します。
論理式と真理値表
論理式は、論理演算子、任意の個数の論理変数、括弧や定数を組み合わせた計算式です。論理回路は、論理式の変数を入力、演算子をそれぞれのゲートに置き換えることで構成できます(これだけが論理回路の構成要素ではありませんが)。
真理値表は、上の3つの演算で用いた表のように、入力と出力の組み合わせとそれに対応する出力を列挙した表です。入力と出力の組み合わせを論理式を用いてを表現すると計算の順番などを変えることで複数通りの表現ができてしまいますが、真理値表は、組み合わせのすべてを列挙しているので一意に表現できます。
論理式には積和標準形と呼ばれる表現方法があります。すべての変数の否定を含む積の項とそれらの項の論理和で論理式を表現します。真理値表が与えられたとき、出力が1となる入力の組み合わせを論理積の項としてそれらの項の論理和をとると積和標準形の論理式が得られます。
1ビットのたし算(半加算器と呼ばれます)を例に説明します。
入力は2つの変数 A、B です。出力も2つの変数で S、C とします。S は足し算の結果 (Sum) で、C は桁上げ出力 (Carry) です。半加算器の真理値表は下の通りになります。S と C それぞれを分けて表にしました。
| \(A\) | \(B\) | \(S\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| \(A\) | \(B\) | \(C\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
S が 1 となるのは (A, B) が (1, 0) か (0, 1) の場合です。
C が 1 となるのは (A, B) が (1, 1) の場合です。この場合、和の結果は 0 となり桁上げが発生するため C が 1 になります。
S を積和標準形の論理式で表すと \(S = (A \cdot \overline{B}) \lor (\overline{A} \cdot B)\) です。
C を積和標準形の論理式で表すと \(S = A \cdot B\) です。
これを回路図で書くと下の図になります。論理式の演算を NOT、AND、OR のゲートに置き換えています。
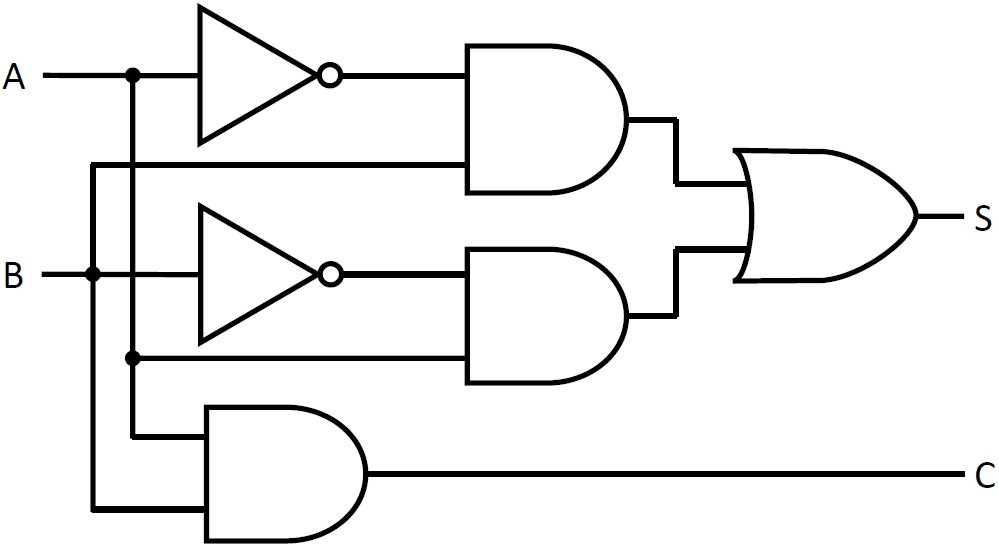
この回路は6個のゲートを使っていることがわかります。
S を別の論理式で表現して、\(S = (A \lor B) \cdot \overline{A \cdot B}\) としてみましょう。こうすると、C の計算に必要な \(A \cdot B\) が S でも利用できて回路図にすると下の通りになります。
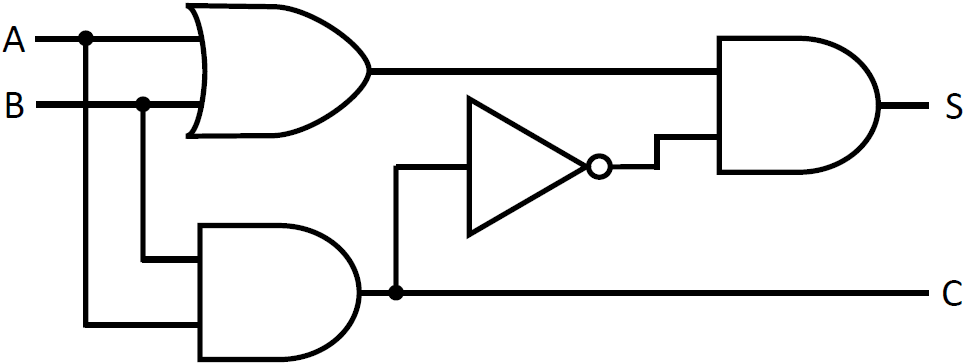
この回路のゲートは 4 個になりました。このように、1 つの真理値表は異なる論理式で表現できて、それらから構築される論理回路も異なる構造になります。
よく使われる論理演算
NOT、AND、OR のほかによく使われる論理演算として、NAND、NOR、EXOR を紹介します。
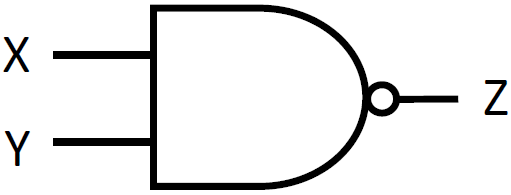
NAND 演算は、AND 演算の否定です。真理値表と回路図での記号は下の通りです。
| \(X\) | \(Y\) | \(Z\) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
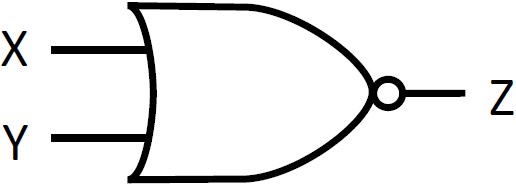
NOR 演算は、OR 演算の否定です。真理値表と回路図での記号は下の通りです。
| \(X\) | \(Y\) | \(Z\) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
EXOR 演算は、排他的論理和 (Exclusive OR) と呼ばれる演算で、2 つの変数のどちらかが 1 の場合にだけ 1 となる演算です。真理値表と回路図での記号は下の通りです。
| \(X\) | \(Y\) | \(Z\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
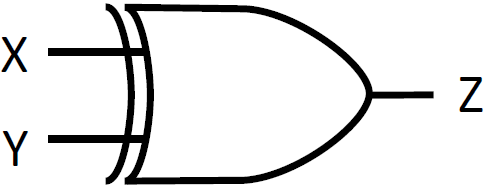
CMOS と呼ばれる方式の論理回路では、論理ゲートはトランジスタと呼ばれるスイッチを用いて構成されます。また、AND ゲートより NAND ゲート、OR ゲートより NOR ゲートの方が効率のよいゲートになります。そのため NAND、NOR ゲートがよく使われます。
EXOR も頻繁に使う演算です。例えば半加算器では、和の出力である S は EXOR です。論理回路のゲートとしては他のゲートを組み合わせて構成します。
3入力以上の論理ゲート
AND、OR (NAND、NOR も同様) ゲートは 3 入力以上に拡張することができます。このときの AND 演算はすべての入力が 1 の場合に出力が 1、他の場合は 0 となります。OR 演算はすべての入力が 0 の場合に出力が 0、他の場合は 1 となります。
3 入力の AND 演算の真理値表と回路図での記号は下の通りです。
| \(A\) | \(B\) | \(C\) | \(Z\) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
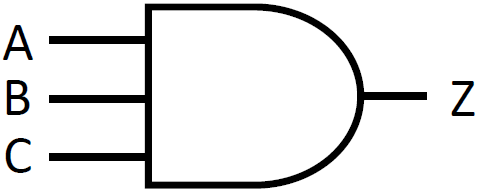
3 入力の OR 演算の真理値表と回路図での記号は下の通りです。
| \(A\) | \(B\) | \(C\) | \(Z\) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
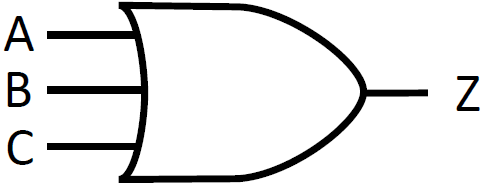
FPGA ではどうなる?
論理回路は、論理式の演算子を論理ゲートに置き換えることで構成できます。一般に、半加算器の例のようになるべく少ないゲート数で回路が構成できればより良い回路になります。ゲート数が少ないということは、用いるトランジスタ数が少ないということで、回路の面積や消費電力が小さくなります。
それでは、FPGA の場合にはどうなるでしょうか?
FPGA では、計算したい論理式があったときに、そこから論理ゲートに変換して回路を構築するわけではありません。FPGA には重要な構成要素であるルックアップ・テーブル (Look-Up Table、 LUT) と呼ばれる回路がたくさん搭載されています。
LUT は、任意の真理値表の入力と出力の組み合わせから選んだ1つを実行する回路です。LUT が書き換え可能で、様々な真理値表を実現できるため FPGA は書き換え可能なハードウェアと呼ばれています。
LUT の入力と出力の数は、用いる FPGA の種類によって異なります。例えば、6 入力 1 出力の LUT であれば、入力が 6 変数、出力が 1 変数の任意の真理値表の回路を書き込めます。入出力の数さえ足りていれば、複雑な論理式で表される演算も 1 つの LUT で実行できます。より多くの変数が必要な論理式は、複数の LUT を組み合わせて実現します。
まとめ
FPGA を使いこなすために理解しておきたい論理回路の基礎を 4 ビットカウンタを題材に学ぶコースの第 1 回として、論理演算と論理ゲートの記号 (シンボル) を紹介しました。次回はクロックやフリップフロップを紹介します。また、同期回路について説明していきます。
東工大 佐藤真平