愛知工業大学の藤枝です。今期は2つのコースを担当することになりました。
普段は FPGA を使って何か面白いことをしたいと思って研究を進めているのですが、縁あってここ数年ほど、 FPGA の素子を使った 真性乱数生成器 (TRNG; True Random Number Generator) の設計法やその応用について研究しています。このコースでは、そもそも乱数って何?というところから、TRNG に求められる要件、また FPGA 向けのいくつかの TRNG の設計について、ACRi ブログの読者の皆さんにご紹介したいと思います。
予備知識がほとんどなくても読める説明を心がけていきますが、FPGA の内部構造や順序回路のタイミング制約について、先に「4ビットカウンタでわかる FPGA のための論理回路 入門」に目を通しておくと、内容の把握がしやすいかと思います。アナログ回路の知識や確率・統計の知識も、ちょっとだけ必要です。
そもそも乱数とは?
乱数に求められる性質
乱数、英語でいうと Random Number ですが、この Random は「でたらめの」とか「無作為の」と訳すことができます。ここでは、次に出力される値に対して、(それがある値になる確率はわかるにせよ) どの値が出てくるかがわからない、という意味です。
例えば、6面のサイコロを振った場合、サイコロ自体やその投げ方に細工がされていない限り、ある出目が出る確率はどの目も 1/6 ですし、次にどの目が出るかは予測できません。同様に、6面のサイコロを2個振った時の出目の合計を考えると、2になる確率は 1/36、7になる確率は 1/6 で均等ではありません。
しかしながら、次の値はあくまでその確率に従って出てくるもので、やはり予測はできません。サイコロ2個を使った有名なカジノゲームにクラップスがありますが、もし次の出目が多少なりとも予測できたとしたら、大金持ちになれてしまいますね。

この「次の値が予測できない」ということを予測不可能性といいます。これを達成するには、少なくとも出力される値に規則性 (パターン) があってはなりません。逆に、一般の用途であれば、出力に規則性がなければ十分な場合がほとんどです。
コンピュータは2進数を使いますから、コンピュータにとっては ‘0’ と ‘1’ のビットが等確率で、かつ規則性なく並んだビット列を乱数列として扱えると都合が良いです。このようなビット列を生成する回路や機器などを乱数生成器といいます。英語だと Random Number Generator ですが、ビット列であることを強調する場合には Random Bit Generator という場合もあります。
擬似乱数生成器 (PRNG)
さて、今「回路や機器など」と書きましたが、規則性のないビット列はアルゴリズムによって作り出すこともできます。これを疑似乱数生成器(PRNG; Pseudo-Random Number Generator) といいます。
PRNG は「内部の状態をもとに、ある決められた方法で計算を行い、次の状態を求めるとともに、その結果を出力する」ものだと捉えることができます。つまり、ディジタル回路の文脈で言えば、PRNG は下図に示す一種の順序回路であるといえます。
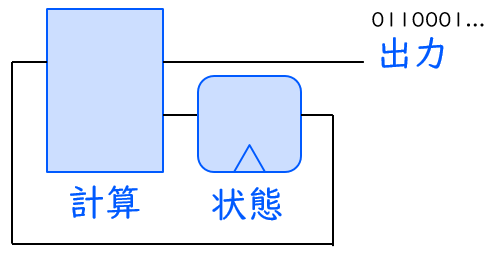
とりうる状態の数は有限ですから、PRNG の出力は非常に長い目で見れば規則性・周期性があると言えます。ただその周期が十分に長ければ、実用上は規則性がないとみなせます。例えば、多くの現代的なプログラミング言語で使われている PRNG のアルゴリズムにメルセンヌ・ツイスタがありますが、その周期は 219937 – 1 と事実上無限といってもよい長さになっています。
ただプログラミング言語やライブラリによっては、周期があまり長くなかったり、特定のパターンを持ってしまうアルゴリズムを使っている場合があります。このような「質の悪い」PRNG を不適切に使ってしまうと、例えばサイコロの出目が重要なボードゲームであるにもかかわらずその出目が偶数と奇数を繰り返すなどといった、重大なバグの原因になることもあります。
乱数とセキュリティ
真の意味での予測不可能性
では、出力に規則性がなければそれで常に問題ないかというと、そうではありません。PRNG は今の内部状態から計算で次の出力を求めるので、もしも何らかの方法で内部状態が知られてしまうと、次の出力もわかってしまうことになります。
その方法は、それまでの出力列を観察することかもしれませんし、対象がソフトウェアのアルゴリズムであれば初期状態の作り方を解析したり、メモリの内容を盗み見ることかもしれません。あるいは、動作時間、消費電力、漏洩する電磁波などといった動作中の挙動を観察することで、内部状態が推測できるかもしれません (サイドチャネル攻撃といいます)。
例えば、PRNG の初期状態がシステムの現在時刻により設定されていることがわかっていたとすれば、システムの現在時刻を特定の時刻に設定して、プログラムの起動後から一定の操作をすることで、ある時点で自分の望んだ乱数を得ることが可能かもしれません。いわゆる「電源パターン」とか「乱数調整」とよばれるものです。
これがゲームのハイスコアや狙ったモンスターを得るためのものであれば (良くはないにしても) まだかわいいものです。仮にこれがセキュリティ用途で使われるもの、例えば暗号の鍵であったら?と考えれば、PRNG では不十分な場合があるということが想像できるかと思います。そこで必要なのが真の意味での予測不可能性であり、それを利用した乱数生成器が真性乱数生成器 (TRNG) です。
真性乱数生成器 (TRNG)
TRNG は、物理現象の挙動の不確定性を抽出して、それをビット列として出力する回路や機器のことをいいます。こうした挙動は理論的・本質的に予測不可能なものなので、そこから出力される乱数もまた、予測不可能なものになります。
もちろんその出力自体を乱数として使う場合もありますが、一般に TRNG での乱数の生成スピードは PRNG ほど高くはありません。高速かつセキュリティが求められる場合には、「PRNG の初期状態を設定するために TRNG の出力を使う (またその後も状態を時々 TRNG の出力で上書きする) 」というハイブリッドな方法が使われることもあります。
どのような物理現象を用いるかは様々です。FPGA、ディジタル回路という文脈を離れれば、抵抗器の熱雑音であったり、無線通信路のノイズ成分であったり、原子核崩壊であったりします。こと FPGA という文脈で言えば、その内部の素子である LUT (Look-Up Table) やフリップフロップ、クロッキング素子などをうまく活用していくことになります。
とはいえ、普通にディジタル回路を組んでいただけでは、当然ながら信号の値は ‘0’ か ‘1’ かに定められることになるので、そこから予測不可能な乱数は出てきません。誤解を恐れずに言えば、必要なのはディジタル回路の素子をあえて誤動作させることです。これにより、素子のアナログな挙動を引き出して、そこから乱数を取り出すのです。
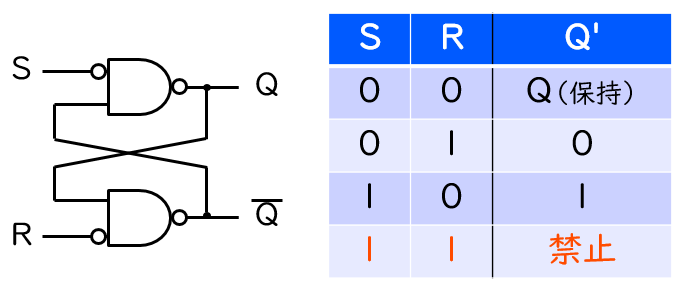
例えば、上図に示すのは、ほぼ全てのディジタル回路の教科書に書かれているであろう SR ラッチ (慣例的に SR フリップフロップとよぶことも多い) です。この回路で入力 S と R が同時に ‘1’ になることは禁止されている、その場合の出力は不定として扱う、といったことを習った方は多いかと思います。
では、この禁止状態を使うと何が起きるでしょうか。より具体的には、禁止状態から S と R を同時に ‘0’ にして、保持状態へ無理やり移行させると何が起きるでしょうか。答えは、’0′ と ‘1’ が半々の確率で出てくる……と言いたいところですが、話はそこまで単純ではありません。そこからもうひと工夫すると SR ラッチからも TRNG が作れるのですが、この話はまたコースの後半でお話することにします。
乱数生成器の評価基準
統計的検定による規則性のなさの確認
ここからは、乱数生成器の良し悪しを決める基準について見ていきます。先に説明した通り、PRNG にしろ TRNG にしろ、乱数には少なくとも規則性がないことが求められます。まずはそのこと (厳密には、規則性があるとする証拠が見つからないこと) を実際に得られたビット列から確認する必要があります。
これには統計的検定、いわゆる仮説検定を用います。ここでは、帰無仮説として「ビット列に規則性はない」という仮説を立てます。もしこの帰無仮説が棄却されるのであれば、対立仮説である「ビット列に規則性がある」という仮説が採択されること (つまり、その乱数生成器は NG ということ) になります 。
この仮説のもとで、得られたビット列に対して一定の計算により統計量を求め、それと等しいかより極端な統計量が得られる確率 (p 値)を求めます。もしこの確率が極めて小さいのであれば、帰無仮説のもとではありえないことが起きたとして、帰無仮説を棄却します。
例えば、1,000ビットのビット列に対して、’0′ の出現数と ‘1’ の出現数のうち、より大きい方の数を求めてみます。もし乱数生成器が ‘0’ と ‘1’ とを等確率で出力しているとすれば、この数の分布は以下のグラフに示すものとなります。当然ながら、500付近が得られる確率は高く、それより大きくなるほど確率は低くなります (また、500ぴったりも少し確率が低いです)。
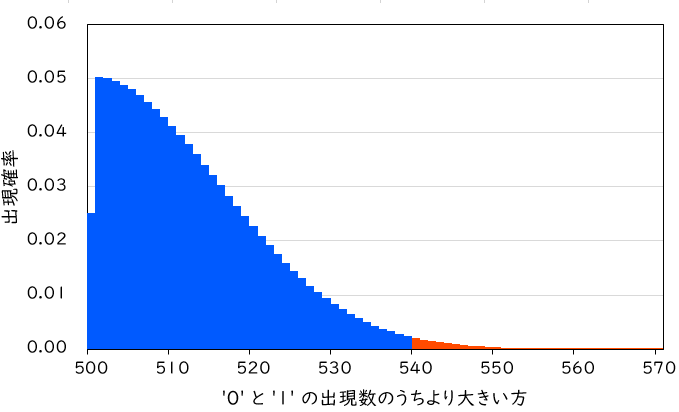
ここでは、実際には ‘0’ が 540 個、’1′ が 460 個得られたとします。このときの p 値は、出現数のうち大きい方の数が 540 以上になる確率ですから、グラフの赤色で示した部分を足し合わせたものになります。実際にこれを求めてみると、p 値は 0.01244 となりました。
こうした検定を様々な観点から行っていき、どの観点でも帰無仮説が棄却できなかった、つまり規則性があるという証拠が見つからなかった場合には、そのビット列を生み出した乱数生成器は「合格」ということになります。こうした試験方法は、米国 NIST の SP800-22 で規定されたテストスイートをはじめとして、いくつか存在しています。例示した ‘0’ と ‘1’ の出現頻度を用いた検定も、実は NIST のテストの一種になっています。
なお、NIST のテストの場合、1,000,000 ビットのビット列 x 1,000 個に対して20種類弱の検定を行い、検定ごとに「得られた p 値の分布に偏りがない」ことを帰無仮説として合否を判定することを推奨しています。これはかなり厳しい条件で、少しでも規則性の兆しが見られればあっさり帰無仮説が棄却されてしまいます。本来、帰無仮説が棄却できないことは帰無仮説が正しいこととイコールではないですが、なるべくイコールになるような工夫がされているのです。
確率的モデル
上述した NIST のテストは多くの TRNG の研究で使われている一方で、真の意味での予測不可能性は、これだけでは証明できません。最近の TRNG では、出力が十分な不確定性 (エントロピー) をもつことを、確率的モデルとともに示すことが、しばしば求められます。現に、こうしたモデルの存在は、ドイツ BSI による AIS-31 規格 における TRNG の要件の1つとなっています。
【2022-10-05 追記】上記 URL が変更になっていたため、修正しました。
ここでは、まず TRNG が利用する物理現象の挙動を、何らかのパラメータとともにモデル化します。このパラメータは何らかの測定の結果からフィッティングによって求められるものにしておきます。そこから TRNG が ‘1’ のビットを出力する確率を求め、それが0.5に十分近いことを確かめます。
こうしたモデルの作成に求められるセンスは、回路設計というよりは、むしろ物理や数学のそれに近く、モデルの作成自体が独立した研究として成立します。その意味で、モデルの作成そのものを気にすることはあまりないかもしれません。ただ、既存の確率的モデルをもつ TRNG を改良した場合には、それが既存のモデルに適合しているかどうかには注意する必要があるでしょう。
その他の評価基準
TRNG のその他の評価基準としては、回路面積や乱数の生成速度、デバイスや環境への非依存性などがあります。
一般の計算回路でもそうですが、回路面積は小さいに越したことはありません。FPGA の場合は、使用した LUT やフリップフロップの個数で評価することになります。乱数の生成速度については、あまりに低速だと PRNG と組み合わせることが前提となってしまい、回路面積を余分に必要とするため、望ましくありません。
デバイスや環境への非依存性というのは、デバイスや環境が異なっていても、問題なく動作する (予測不可能な乱数を出力できる) ことを指します。FPGA 上の TRNG の場合、素子のアナログな挙動が問題になるので、たとえ同じコンフィグレーションファイルを書き込んだとしても、チップによってその挙動は異なるかもしれません。うまく行くまで素子の配置を変えてやり直すという方法もありえなくはないですが、その調整作業がチップごとに必要であっては、実用性があるとは言えないでしょう。また、外部環境に依存しないことは、外部からの攻撃を防ぐ意味でも重要です。
まとめ
今回は、TRNG に関する基礎知識として、PRNG との違いや、TRNG に求められる性質について解説しました。今回の要点は以下のとおりです。
- 乱数には予測不可能性が求められる。一般には出力に規則性がなければ十分だが、特にセキュリティ用途で使う場合には、真の意味での予測不可能性が必要である。
- 物理現象から生成され、予測不可能な乱数を生成する回路や機器を TRNG とよぶ。
- TRNG の評価基準には、回路面積、生成速度、ランダム性やそれを裏打ちする確率的モデルの有無、デバイスや環境への非依存性などがある。
次回は、FPGA の回路素子を用いた TRNG に関するサーベイ論文を土台に、FPGA 向きの TRNG の生成手法について概説したいと思います。
愛知⼯業⼤学 藤枝直輝