FPGA と予測不可能性と乱数 (3)

FPGA 向けの真性乱数生成器 (TRNG) の設計法に関するコースの第3回です。今回は、前回に COSO 型、PLL 型の TRNG として紹介した、コヒーレントサンプリングを用いた TRNG やその利用のコツについて詳しく説明します。

なお、この記事で紹介する PLL 型の TRNG を Xilinx 社の最近の FPGA で扱う方法 [1] についての詳細は、記事公開月の月末 (2020年11月) に開催される、日本発の計算機・ネットワーク関連の国際会議である CANDAR の PDAA ワークショップで発表します。

コヒーレントサンプリングの原理と実際

コヒーレントサンプリングの原理

前回紹介したコヒーレントサンプリング型 (COSO 型および PLL 型) の TRNG のブロック図を再掲します。いずれの場合でも、少しだけ異なる周波数をもったクロック信号を、D フリップフロップ (D-FF) のデータ入力とクロック入力に接続します。

コヒーレントサンプリング型 (COSO 型) の TRNG [2] の再掲。
PLL を用いたコヒーレントサンプリング型 (PLL 型) の TRNG [2] の再掲。

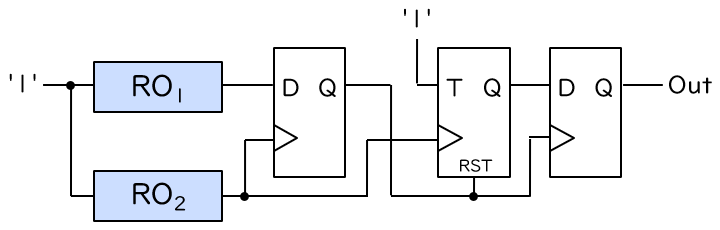
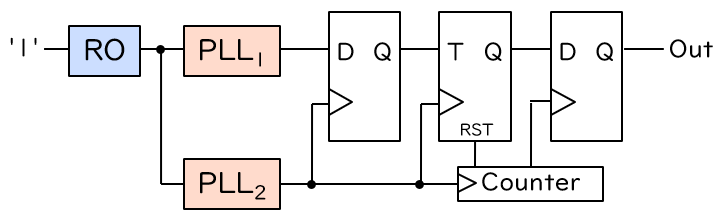
ここでは、D-FF のデータ入力に与えられるクロックを Clk1、クロック入力に与えられるクロックを Clk2 とします。D-FF の動作の定義上、Clk2 が立上る (‘0’ から ‘1’ になる) たびに、その瞬間の Clk1 の値が D-FF の出力として取り込まれることになります。

以降では簡単のため、2つのクロックの周波数の比を N + 1 : N と仮定します。N には数百程度の大きな値を使います。つまり、Clk2 が N 回立上るまでの間に、Clk1 は N + 1 回立上ります。この様子を下図に示します。

2つのクロックの周波数比を N + 1 : N と仮定する。

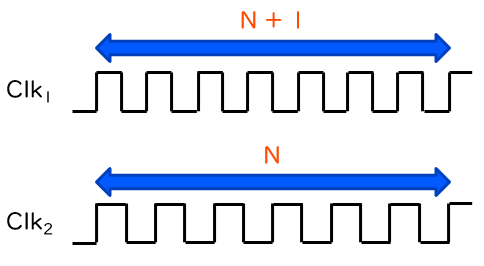
いま、ある時刻において、Clk1 と Clk2 が同時に立上りました。D-FF では Clk1 の立上りの瞬間を取り込みます。そこから、次に Clk2 が立上るまでのクロック信号のタイミングチャートを下図に示します。

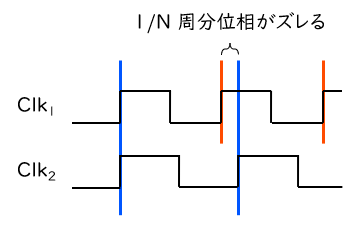
サンプルのたびに Clk1 と Clk2 との間の位相は少しずつズレる。

ここで、Clk1 の立上りを赤線で、Clk2 の立上りを青線で示しています。周波数比を N + 1 : N と仮定したので、Clk2 の1周期は Clk1 の (N + 1) / N 周期、つまり 1 + (1 / N) 周期に相当します。そのため、Clk2 が次に立上った時、Clk1 から見れば 1 / N 周分だけ位相がズレた信号が取り込まれることになります。同様に、そこからもう1度 Clk2 が立上がれば、2 / N 周分位相がズレた信号が取り込まれます。

これを N 回繰り返すと、位相のズレはちょうど1周して (N / N になり) 元に戻ります。そして、このとき取り込んだ信号の系列は、ちょうど Clk1 の1周期分の波形を、N 分割してサンプリングしたものと原理上等しくなります。これがコヒーレントサンプリングです。周期的な信号の波形を高い時間精度でサンプリングしたい時には、よく利用されるテクニックだそうです。

さて、Clk1 の1周期分の波形というのは、(デューティ比が 50% であれば) 半周期分の ‘1’ と半周期分の ‘0’ です。結局のところ、原理上 D-FF から出力されるサンプリング結果は N / 2 個の ‘1’ の連続と N / 2 個の ‘0’ の連続の繰り返しとなります。

コヒーレントサンプリングの実際

ただ実際には、これらサンプリング結果における ‘0’ や ‘1’ の個数は不確定性をもちます。1つの理由は、クロック信号の立上り・立下りのタイミングは一定ではなく、ある程度のばらつきをもつことです (前回も取り上げたジッタです)。Clk1 の立上り・立下り付近を取り込む際は、実際に立上り・立下りがいつ来たかによって、’0′ が取り込まれるか ‘1’ が取り込まれるかが変わります。

もう1つの理由は、D-FF には「クロック入力の立上りの前後の一定時間は、データ入力の値を変更してはならない」というルールがあることです。これを破った場合の出力値は保証されません。最悪の場合には、’0′ と ‘1’ の中間を取り込んでしまうこともあります (メタスタビリティ)。

下図はこれらの要因を図示したものです。理論上はある時刻 (図の青い点線) ではっきりと信号値が ‘0’ から ‘1’ に切り替わると想定できたため、あるサンプルでは D-FF は ‘0’ か ‘1’ のどちらか決まった値を取り込めると考えることができました。しかし、実際には立上り・立下りの前後で D-FF が ‘0’ と ‘1’ のどちらを取り込むかは確率的になります。例えば立上りの前後では、D-FF が ‘1’ を取り込む確率は、立上りの少し前から少し後の間で 0 から 1 へとゆるやかに移行する (図の赤線) ことになります。

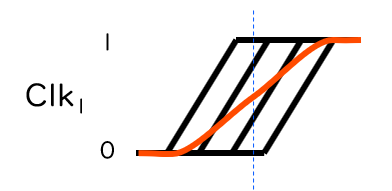
Clk1 の立上り・立下り付近では、’0′ と ‘1’ のどちらが取り込まれるかは確率的である。

そのため、サンプリング結果の ‘0’ あるいは ‘1’ の個数を数えると、その下位ビットには ‘0’ と ‘1’ がほぼ半々で現れ，かつどちらが現れるかは予測できません。コヒーレントサンプリングを用いた TRNG では、これを乱数として取り出します。

コヒーレントサンプリングを用いた TRNG の検討事項

‘0’ や ‘1’ の個数をどう数えるか？

ここからは、コヒーレントサンプリングを用いた TRNG を実際に構築するにあたって考えるべき事項を見ていきます。なお、以降の説明では TRNG はサンプリング結果の ‘1’ の個数を数えるものとします。’0′ を数えるとした場合でも、’1′ と ‘0’ とを反転して読み替えればよいので、一般性は失われません。

先に ‘1’ の個数を数えると書きましたが、実際の数え方には

  • 連続する ‘1’ の個数を数える方法
  • N 回のサンプリング中の ‘1’ の個数を数える方法

の2通りが考えられます。最初に再掲したブロック図では、COSO 型が前者の方法、PLL 型が後者の方法に基づいて回路を構成しています (なお、COSO 型の図は ‘0’ の数を数える回路となっています)。

前者の方法では、連続が途切れた時点で T フリップフロップ (T-FF) をリセットし、その直前の T-FF の出力値を TRNG の出力として採用できます。これは、必要な回路素子の数の少なさの面で有利です。

しかし、連続する ‘1’ の個数が極めて少なくなる可能性があることに注意が必要です。その例を下図に示します。先に述べた通り、Clk1 の立上り・立下りの前後をサンプリングするとき、D-FF が ‘0’ と ‘1’ のどちらを取り込むかは確率的です。そのため、この区間では ‘0’ と ‘1’ が混ざり合う、つまり、’0′ (‘1’) の中に ‘1’ (‘0’) が現れることがあります。

Clk1 の立上りでは、’0′ の連続の中に ‘1’ が現れる場合がある。

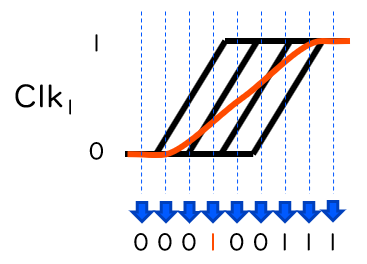
こうした少ない個数の ‘1’ の連続は、そうでない (N / 2 個前後の) ‘1’ の連続よりも少ない不確定性 (エントロピー) しか持ちません [3]。そのため、これらは出力ビット列の規則性のなさに悪影響を及ぼす場合があります。

一方、後者の方法では区間内の ‘1’ の数の合計を数えることになるので、こうした問題は生じません。また、乱数は Clk2 の N サイクルごとに出力されるので、Clk2 の周波数と N の値がわかっていれば、乱数の生成速度が計算できることになります。ただし、後者の方法は周波数の比がわかっている場合、つまり PLL 型の TRNG でしか使えません。

周波数の比率をどう定めるか？

周波数の比率、つまり N の値は、乱数の不確定性と生成速度の両方に影響します。N が大きければ、それだけ Clk1 の波形を細かくサンプリングすることになるので、’1′ の個数の不確定性も大きくなります。一方で、乱数の生成速度は N に反比例して小さくなります。したがって、これらはトレードオフの関係にあります。

N が最低限どの程度大きくあるべきかは、クロック信号のジッタの大きさにも左右されます。いくつかの研究を見るに、また私の経験上、COSO 型の TRNG では N は少なくとも100程度、PLL 型では250程度は必要なようです。コヒーレントサンプリングを用いた TRNG を構築するときは、これを満たす範囲で、N が十分小さくなるような配置やパラメータを探ることになります。

PLL 型: クロッキング素子のパラメータをどう定めるか？

PLL 型の TRNG では、FPGA にあらかじめ用意された PLL (Phase-locked Loop) などのクロッキング素子を使います。これらはメーカーや世代によって作りが変わっていることが多く、それらに合わせた調整も必要です。

このことを説明するために、まずは PLL の基本構成について下図を用いて説明します。PLL は、位相周波数検出器 (PFD; Phase Frequency Detector)、チャージポンプ、ローパスフィルタ (LPF)、電圧制御発振器 (VCO; Voltage Controlled Oscillator)、それと下図の青色で示すいくつかの分周器から構成されます。

PLL (Phase-locked Loop) の基本構成。

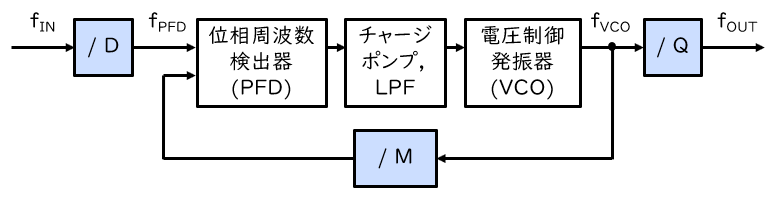
分周器の分周比をそれぞれパラメータ D、M、Q で示します。なお、Xilinx 社のドキュメントでは Q は O (オー) と表記していますが、0 (ゼロ) との混同防止のためここでは Q としています。

PFD から VCO までの一連の回路は、PFD に入力された2つのクロックの周波数を等しくするためのフィードバック回路です。そのため、入力クロックを分周して得られた基準クロックの周波数を fPFD、VCO の出力周波数を fVCO とすると、fPFD = fVCO / M、つまり fVCO = M・fPFD の関係が成り立ちます。これより、入力周波数・出力周波数をそれぞれ fIN、fOUTとすると、

  • fPFD = fIN / D、
  • fVCO = M・fIN / D、
  • fOUT = M・fIN / (D・Q)、

の関係が成立します。

ただし、パラメータとして設定可能な値の範囲は決められていますし、これらの周波数にはいずれも上限・下限が定められています (データシートに明記されています。例えば Artix-7 なら文書番号 DS181)。こうした制約の範囲で、適当なパラメータを設定することになります。

クロッキング素子のパラメータ選択の例

我々の研究 [1] では、Xilinx 社の最近の FPGA に搭載されているクロッキング素子である MMCM (Mixed-Mode Clock Manager) を使用して、PLL 型の TRNG の構築を試みました。MMCM では、M や Q の値として、整数だけではなく 1/8 刻みの分数も選べるようになっています。そのため、選べるパラメータの幅が大きく広がっています。

まずは、少し前の世代の FPGA である Virtex-5 向けに提案された PLL 型の TRNG の先行研究 [4] をベースに、最低限のパラメータの修正を行うことで移植を試みました。しかし、それだけでは良質な乱数を生成することはできませんでした。次回紹介する別の研究でもそうだったのですが、新しい FPGA はより誤動作しにくいように作られているので、既存の方法を新しい FPGA にそのまま適用しようとするとうまくいかない、ということがよく起こります。

そのため我々は、MMCM のパラメータ選択の自由度を最大限に活用して、良質な乱数を高速に生成できるパラメータの組を見つける手法を検討しました。そして、実際にその手法を用いて132通りの有力なパラメータ候補を見つけ出しました。その一例を下表に示します。なお、入力クロックとして 100 MHz の外部クロックを直接利用しています (つまり、fIN は 100 MHz です)。

IDクロックMDQfOUT [MHz]
1Clk160.000101.000600.00
Clk259.00088.62585.51
2Clk163.750101.000637.50
Clk262.500106.87590.91

周波数比が N + 1 : N ではないことに気づくかもしれませんが、これも工夫の1つです。上に示した2つの候補では、Clk1 の周波数を 1/7 にすることで、周波数比は N + 1 : N の形になります。

こうして得られたパラメータ候補を使って PLL 型の TRNG を構成し、得られたビット列を AIS-31 規格の手順 B に定められた試験にかけたところ、おおよそ 2/3 にあたる89個の候補で「合格」となりました。また、乱数の生成速度の平均は 1.18 Mbit/s となりました。これは、単純な移植と比べると、「合格」した候補の数も乱数の生成速度もおおよそ10倍にあたります。

以上より、新しいクロッキング素子を活用したことで、単に既存の手法が新しい FPGA で利用可能になったということを超え、新たな価値を提供することができました。

まとめ

今回は、FPGA におけるコヒーレントサンプリングを用いた TRNG について詳しく紹介しました。今回の要点は以下のとおりです。

  • ある周期的な信号を、それと周波数が少しだけ異なるクロックでサンプリングする手法を、コヒーレントサンプリングとよぶ。
  • コヒーレントサンプリングで立上り・立下り付近をサンプリングするとき、’0′ と ‘1’ のどちらが取り込まれるかは確率的であり、このことが TRNG に応用される。
  • クロッキング素子を用いる場合 (PLL 型) は、素子のパラメータ選択の自由度を活かすことが重要である。

次回からは、SR ラッチの禁止状態に着目した TRNG の詳細と、その構成方法を扱います。

愛知⼯業⼤学 藤枝直輝

参考文献

  • [1] N. Fujieda and S. Takashima: Enhanced use of mixed-mode clock manager for coherent sampling-based true random number generator, 12th International Workshop on Parallel and Distributed Algorithms and Applications (PDAA-12) held in conjunction with CANDAR ’20, accepted, 2020.
  • [2] O. Petura, U. Mureddu, N. Bochard, V. Fischer, and L. Bossuet: A Survey of AIS-20/31 Compliant TRNG Cores Suitable for FPGA Devices, 26th International Conference on Field Programmable Logic and Applications (FPL 2016), pp. 1–10, 2016. DOI: 10.1109/FPL.2016.7577379
  • [3] N. Fujieda, M. Takeda, and S. Ichikawa: An Analysis of DCM-based True Random Number Generator, IEEE Transactions on Circuits and Systems II: Express Briefs, Vol. 67, No. 6, pp. 1109–1113, 2020. DOI: 10.1109/TCSII.2019.2926555
  • [4] A. P. Johnson, R. S. Chakraborty, and D. Mukhopadyay: An Improved DCM-Based Tunable True Random Number Generator for Xilinx FPGA, IEEE Transaction on Circuits and Systems II: Express Briefs, Vol. 64, No. 4, pp. 452–456, 2017. DOI: 10.1109/TCSII.2016.2566262
タイトルとURLをコピーしました