みなさんこんにちは。本シリーズ「FPGA で作る暗号は危険 ?」では、FPGA 内で暗号機能を実現する方法とその危険性を解説していきます。
前回までは共通鍵暗号 (AES 暗号) を中心に FPGA への実装方法やサイドチャネル攻撃について解説しました。今回からは公開鍵暗号について触れていきます。
ただし、公開鍵暗号については具体的な暗号の実装方法というよりも効率的な処理を行うために欠かせない処理を解説していきます。 今回の記事は数式が多い内容になりますが、決して難しい数学ではないのでお付き合い下さい。
公開鍵暗号と共通鍵暗号の実装方法による違い
暗号の仕様が作り上げられるとき公開鍵暗号、共通鍵暗号のいずれも数学が利用されています。
しかし、共通鍵暗号である AES 暗号を FPGA に実装するためにはそれらベースとなっている数学を理解する必要はなく、データ変換のやり方 (データの置換と XOR のみ) が分かれば組み込むことができました。
共通鍵暗号はマイコン等での実装が仕様設計で意識され、重い処理 (演算) を使わず、高速に処理ができるように作られているためです。
それに対して公開鍵暗号は数学的に解くことが困難な問題がベースにして作られている暗号であり、どうしても数式で表現された処理を行う必要があります。
公開鍵暗号は処理に時間が掛かる暗号なので鍵交換やデータの真正性を確認するための認証など、ある程度処理に時間が掛かることが容認される用途で使用されています。容認される用途とはいえ、高速に暗号化 / 復号ができ、使用するロジックサイズが小さい方がより良いものであることは変わりません。
公開鍵暗号では数式の処理を行うため、どうしても数学の演算を組み込むことが必要です。数式の処理をどのように機能として実現していくか (FPGA 内に組み込むか) の方法はさまざまであり、作り手によって性能が大きく変わる部分です。
具体的には、並列処理にする部分とパイプライン処理にする部分をどのように分割するかで演算時間と使用ロジックのバランスが決まってきます。また、数式を変形していく中でどの段階の数式を使うかも最終的な性能に関わってきます。
公開鍵暗号のトレンド
公開鍵暗号として長く使用されてきた RSA 暗号から楕円曲線暗号に移行しているのが現在のトレンドです。
公開鍵暗号のセキュリティ強度は鍵のビット長に比例すると考えることができるため、攻撃側の計算速度が向上することに対応するには鍵を長くする必要があります。
RSA 暗号を安全に使うためには 2048 ビット以上の鍵長が必要とされてますが、そろそろ 2000 ビット級でも危険であり、3000 ビット級が必要な時期が見えてきています。
公開鍵暗号は鍵の各ビットに従った処理を行うため、鍵長に比例して処理時間が長くなってしまいます。3000 ビット級の RSA 暗号は単純計算で 2000 ビット級に対して 1.5 倍の処理時間が必要になり、処理時間の増加が問題視されています。そこで、短い鍵長で同等のセキュリティ強度を持つ楕円曲線暗号 (RSA 暗号の 3072 ビットと楕円曲線暗号の 256 ビットが同等のセキュリティ強度 ) が主流になりつつあります。
巨大な数字の取り扱い
RSA 暗号の鍵長として 2000 ビットとか 3000 ビットといった普段の FPGA では余り使わない大きなサイズのデータが出てきました。公開鍵暗号ではこういった巨大なデータを演算する必要があり、楕円曲線暗号であっても 256 ビットのデータを取り扱います。
大きな数字を演算した結果は更に大きな数字になります。例えば、256 ビットと 256 ビットの掛け算を行った結果は 512 ビットです。この調子で演算を進めていくと際限なくデータが大きくなり、とても実装できるものでは無くなってしまいます。
そこで、暗号の世界では数値の最大値を制限できる仕組みが組み込まれています。数学用語だと色々な言い回しがあると思いますが、あえて数学用語を使わずに使い方だけに絞っていえば、「値 X を固定値 P で割った余り R は元の値 X と同じ値として扱える」という仕組みです。
何かピンとこないかもしれませんが、時刻の最大値を24時としていることと同じです。つまり、時刻25時 (X) は24 (P) で割った余りの時刻1時 (R) と同じとして扱えるので時刻の最大値を24に制限できるというのと同じ原理です。
例えば、P が 256 ビットだと P で割った余りは必ず 256 ビット以下になり、最大のデータ長を抑えることができます。
数学は便利なツール
「ある値で割った余りを使えば…」と簡単に言ったものの、余りを求めるために行う割り算は時間の掛かる処理です。特に大きな値を使った割り算は処理時間が長く、出来れば使うことを避けたいところです。
そこで、大きなデータの割り算のように避けたい処理を軽い処理に置き換えられる仕組みが暗号機能の中に組み込まれている場合があります。
数学を便利ツールとして使う方法は暗号の機能仕様に記載されていないため、数学が得意でないと簡単にはその便利機能に気づきませんが、使わないと損をするような数学が実は取り込まれています。逆に言えば、重い処理を回避できる良い仕組みが組み込まれている暗号が良く使われている暗号ということもできます。
楕円曲線暗号
数学的な便利ツールが組み込まれている例を挙げて説明していきますが、まずはその題材となる楕円曲線暗号について少し解説しておきます。
楕円曲線上にある点 R を暗号鍵に従って足していく演算 (単純な足し算ではなく、楕円スカラー倍算といいます) を s 回 (s が鍵の長さ) 繰り返したときにたどり着く点を P = [s]R とします。このとき、P と [s]R が分かっても s が求まらないという一方向性関数としての特性 (楕円離散対数問題) を利用しているのが楕円曲線暗号です。
楕円曲線暗号とは楕円離散対数問題を使用した暗号全般を指す言葉であり、「どういった楕円曲線を使うか」は規定されていません。そのため、色々な楕円曲線を使用した暗号が公開されています。
その中で、数学的便利ツールを紹介する今回の題材は curve25519 とか、x25519 と呼ばれる以下の曲線を使用した楕円曲線暗号です。
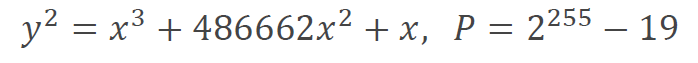
式 (1) で P は余りを求めるときに使用する固定値です。掛け算の結果などでデータが大きくなったときはこの P で割った余りに置き換えることができます。
余りを求める便利な方法
curve25519 を使用した楕円曲線暗号で余りを求める便利な方法を紹介していきます。
因数定理 ( 剰余の定理 )
余りを求めるときに使える数学の定理に因数定理があります。因数定理は高校数学で習う定理ですが、覚えていない人も多いのではないかと思います。
余談ですが、筆者も因数定理を使う必要が出てきた時には全く覚えていませんでした。高校で習うと聞いて、文系の高校3年生だった娘に聞いてみるとバッチリと解説してくれ、娘の成長を感じた瞬間でした。
それはそれとして、因数定理を簡単に書くと「関数 f (x) を x - a で割った時の余りは f (a) になる」というものです。考えてみると単純で、f (x) を x ー a で割った時の商を g (x) 、余りを r とすると以下の式になります。
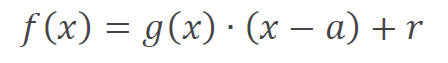
ここで、x = a とすれば、g (x)・(x - a) が消えて、f (a) = r になります。
25519 の妙
curve25519 では余りを取るときは 2255 - 19 で割ることができます。curve25519 の名前にも出てくるこの 2255 - 19 が効率的な処理を行うために設定された絶妙な値です。
上の因数定理と同様に f (x) を 2255-19 で割った時の商を g (x)、余りを r とすると以下の式になります。
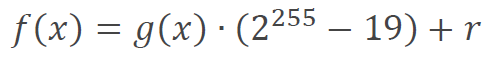
ここで、2255-19 = 0 とすれば、余りの r のみが残ります。2255-19 をもう少し分解すると以下になります。
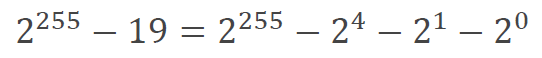
余りを求めるため、2255-19 = 0 とすればよかったので、以下の式が成り立ちます。
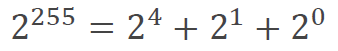
2255-19 を 0 にする部分に違和感を感じるかもしれませんが、上の方で例として挙げた時刻1時と25時が同じであるということと意味合いは同じです。つまり、24時が0 時と同じように、2255-19 が0と同じになります。但し、数学的には 2255-19 = 0 よりも 2255-19 ≡ 0 ( 合同 ) と表現した方が正確ではあります。
乗算結果の余りを求める
暗号処理中に掛け算は何度も行う必要があり、乗算器入力部を必要最低限のデータ長に固定した乗算器を使いたいところです。256 ビットと 256 ビットの掛け算を行った結果の 512 ビットを 2255-19 で割った余り (256 ビット以下) に変換してデータ長を制限することで、256 ビット入力の乗算器を繰り返し使用することができます。
最下位ビットを0桁目として、x 桁目の値を a_x (0 ビット目が a_0、511 ビット目が a_511、以下の図は桁を下付き数字としています) とすれば、512 ビットのデータを以下の式で表すことができます。表記上 、各桁の値を a_x と記号で表していますが、2進数なので a_x は 1 か 0 のいずれかになります。
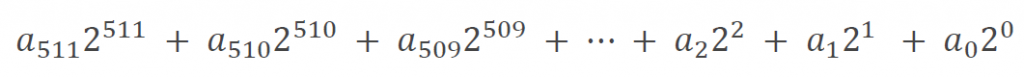
式 (5) を利用するため、511 ビット目から 255 ビット目までをまとめます。
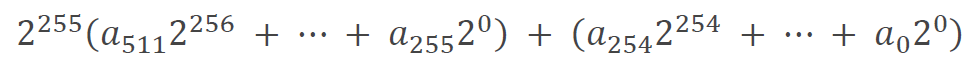
式 (7) に式 (5) を代入します。
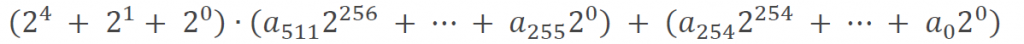
式 (5) を代入した部分を展開します。
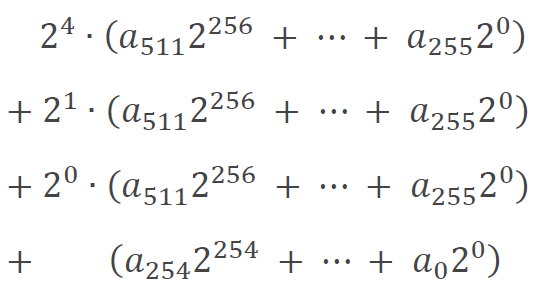
式 (9) に出てくる 24、21、20 はビットシフトなので、各値に従ってビットをシフトして各行を足せば求める値である余りを算出できます。但し、式 (9) で算出した値は 260 ビットになるため、256 ビット以下にするにはもう一度同じ処理を行う必要があります。
この方法を使用すれば、割り算を使わずにビットシフトと足し算のみで余りを算出することができました。「割り算」に比べ、「ビットシフト+足し算」は処理時間が桁違いに短くなります。
暗号処理では加算や乗算を繰り返し行うため、余りを取ってデータ長を小さくする処理をかなりの回数行う必要があり、この処理を高速にできることで暗号処理時間を大幅に短くすることができます。
また、 処理時間の短縮のみでなく、割り算をビットシフトと加算で行えることから DSP の搭載量が少ない FPGA に実装することも可能になります。こういった効率的な実装を助ける仕組みが curve25519 には組み込まれていて、実装方法まで良く考えられた暗号方式であることが分かります。
実際の設計では
複雑な演算を行う必要がある公開鍵暗号ですが、ロジックで機能を実装 (ソフトウェアでの実装であったも同様 ) するときの処理を効率的に行うための工夫が随所に盛り込まれています。しかし、暗号機能に関する論文やネットの記事を見ても、「P を法として合同な整数が… 」とか 「有理群が…」といった数学用語の解説ばかりで数学の苦手な技術者には理解が難しく、組み込まれている工夫に気づくことも簡単ではありません。
一旦その工夫が理解できると「すごい!」と感動するほど良く考えられたものになっていますが、数学的な説明で理解できないような内容を見て、どこに工夫が施されているかをどうやって理解すればよいのか…。
FPGA に公開鍵暗号を実装した事例は余り多くなく、実装方法のノウハウ的な情報は出回っていません。本来であれば、FPGA の技術者が一から公開鍵暗号の処理を理解して、その中にある工夫を汲み取っていくのが良いとは思いますが、数学に対する知識がないと簡単ではありません。
FPGA での実装事例は少ないですが、ソフトウェアでの実装は多くあるため、ソフトウェアの実装例を参考にしたり、その道のプロである大学の研究者などのアドバイスを受けていくのが良いかと思います。
まとめ
今回の記事は数式ばかりになってしまいましたが、公開鍵暗号の主流になりつつある楕円曲線暗号を題材として、数学が便利ツールとして組み込まれている例を解説しました。簡単な式だけで大きな効果が出る工夫が暗号の中には組み込まれていることを理解頂けたかと思います。
AES 暗号のように、FPGA への実装は簡単ですという結論にはなりませんが、組み込まれている絶妙な仕組みに「なるほど!」「面白い!」と思って頂けた方もいらっしゃるのではないでしょうか。
次回は公開鍵暗号に対するサイドチャネル攻撃について解説していく予定です。
株式会社ゴフェルテック 川西紀昭

