みなさんこんにちは。本シリーズ「FPGA で作る暗号は危険 ?」では、FPGA 内で暗号機能を実現する方法とその危険性を解説しています。今回は前回取り上げた公開鍵暗号に対するサイドチャネル攻撃を解説します。また、本シリーズの最終回になりますので、暗号以外も含めたセキュリティについても少し紹介します。
公開鍵暗号に対するサイドチャネル攻撃
第3回で紹介した AES 暗号に対するサイドチャネル攻撃と異なり、公開鍵暗号に対するサイドチャネル攻撃は簡単かつ短時間で行うことができる危険な攻撃です。
公開鍵暗号 (RSA 暗号)
サイドチャネル攻撃を説明する前に攻撃対象となる公開鍵暗号として RSA 暗号の動作を簡単に説明します。尚、以下は攻撃対象となる暗号の動作を説明するための内容で、 RSA 暗号動作の概念のみを示すのでご注意下さい。
公開鍵暗号は数学的な演算を使用する暗号であることを前回説明しましたが、鍵が1の場合と0の場合でこの数学的な演算が異なります。この「鍵によって動作が異なる」という部分に注目してサイドチャネル攻撃が行われます。
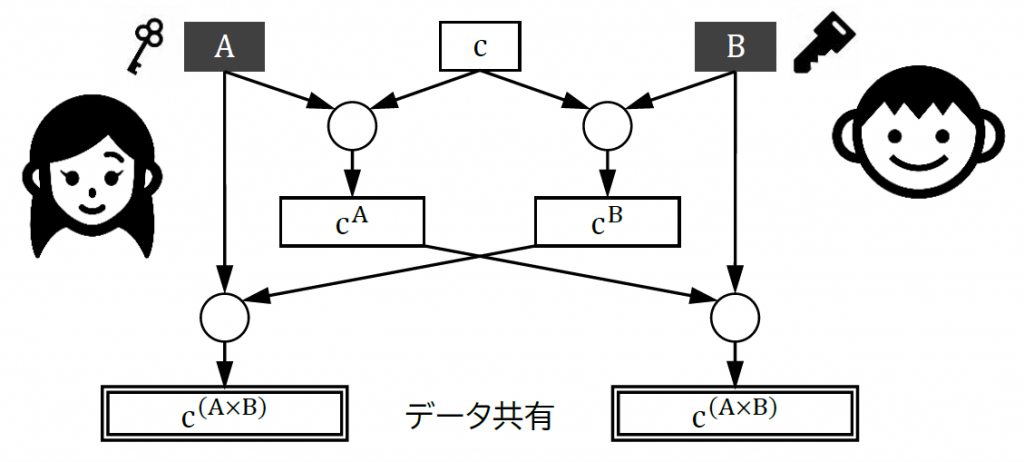
図1は第1回で一方向性関数を使用したデータ共有の説明を行ったときの図ですが、第1回では一方向性関数を簡単に説明するため、演算として掛け算を使いました。今回は公開鍵暗号を説明するため、RSA 暗号で使用されている指数にしています。
アリスとボブは大きな素数 (1028ビット以上 ) である A、B をそれぞれ用意します。お互いに c を自分の素数でべき乗し、べき乗した結果 (cA と cB ) を相手に渡します。相手から受け取った値を自分の素数で更にべき乗することで、双方とも同じ値 (c(A×B)) を共有することができます。
RSA 暗号は離散対数問題という数学で簡単に解くことができない問題を利用しています。離散対数問題とは、共有データである c(A×B) で使用している A と B が十分に大きな素数だった場合、c(A×B) が分かっても A と B を簡単に求めることができない (素因数分解を簡単に行う方法がない) という特性です。
図1は、RSA 暗号を使用したデータ共有の概念を示しているもので、実際の RSA 暗号では他にも色々な処理が必要です。では、RSA 暗号の動作を説明する訳ではないのにわざわざ「べき乗」を使った式に変えたかというと、XY という演算を行う必要があるということを示すためでした。しかも、XY で使用する Y は非常に大きな値です。
バイナリ法
RSA 暗号ではべき乗計算が必要であり、しかも、べき乗として非常に大きな値を使用します。べき乗は掛け算を行う回数なので、ひたすら掛け算を行うことで算出することができます。しかし、掛け算の回数が非常に多い (2000ビット回以上) ため、べき乗回の掛け算で算出する方法は現実的でありません。現実的な時間で処理するためには効率的な演算を行う必要があります。
具体的に 31000 を計算する場合を考えてみます。
31000 は 3 を 999 回掛け合わせれば算出することができます。1000 回程度なら大した時間ではありませんが、2000 ビット以上の回数ではさすがに時間が掛かり過ぎます。そこで、計算量を減らすためバイナリ法という方法を使ってみます。
まず、指数部の 1000 を 2 進数表現に変えます。
指数部に注目し、2進数の上位から順に処理を行います。2進数が1の場合は3を掛けてから2乗、0の場合は2乗のみを行うことでべき乗結果を算出できます。
掛け算のみで算出する場合は掛け算を999回行う必要があった計算をバイナリ法だと掛け算を6回、2乗算を9回行うだけで計算することができ、随分と効率化することができます。
秘密にするのはどこ ?
ところで、例に挙げた 31000 を行うとき、第三者に漏れてはいけない暗号鍵はどの部分でしょうか。攻撃者に漏れてはいけない暗号鍵にあたるのはアリスとボブの秘密鍵から算出した図1の「A × B」にあたる部分、つまり、31000 の指数部「1000」です。
少し脱線しますが、鍵長2048ビットの RSA 暗号では十分な安全性確保が危うくなってきているため、3000ビット以上が推奨されています。バイナリ法で効率化したとしても演算時間は鍵長と共に増加するため、演算を3000回以上の行うにはそれなりの時間が必要です。
それに対して楕円曲線暗号は同等のセキュリティ強度を短い鍵長で確保することができ、演算時間を短縮することができます。
公開鍵暗号のトレンドが RSA 暗号から楕円曲線暗号に移行している理由は、この演算時間の短縮ができることです。
サイドチャネル情報
バイナリ法では暗号鍵である指数部を2進数で表した各ビットに応じて異なった演算処理を行います。処理の違いは消費電流の違いとなり、消費電流の違いがノイズとして電源に漏れ出してしまいます。
共通鍵暗号である AES 暗号に対するサイドチャネル攻撃の場合、パワーモデルとの相関を得るために暗号化動作中の電源ノイズ波形を数多く測定する必要がありました。
しかし、公開鍵暗号をサイドチャネル攻撃する場合、暗号鍵と処理がリンクしている、つまり、暗号鍵と電源ノイズがリンクしているため、1回の測定で鍵そのものを波形から読み取ることができてしまいます。
図4は暗号動作中の電源を測定した波形です。波形にふたつのパターンがあることが分かると思いますが、この2種類がそれぞれ掛け算と2乗算を行っている時のノイズにあたります。電圧が高い部分が2乗算処理中のノイズであり、低い部分が掛け算です。
2乗算のみ行っている波形が暗号鍵 = 0 の処理、掛け算と2乗算がペアで行われている波形が暗号鍵 = 1 の処理であることが分かり、それをそのまま暗号鍵として読み取ることができます。
共通鍵暗号に対するサイドチャネル攻撃のように、数多くの波形取得や取得した波形データを解析する必要が無く、公開鍵暗号に対するサイドチャネル攻撃ではたった1回の波形測定で暗号鍵を盗み出すことができます。
しかも、パワーモデルの算出といった準備も不要であり、暗号化させるときの平文さえなんでも構いません。
つまり、公開鍵暗号に対するサイドチャネル攻撃は簡単であり、対策を施していないと非常に危険だと言えます。
サイドチャネル攻撃対策
暗号鍵によって処理の内容が異なることが原因で鍵情報そのものがサイドチャネル情報として漏れ出してしまいました。そこで、暗号鍵による処理の違いを極力少なくすることでサイドチャネル攻撃対策を行うことができます。
モンゴメリラダー法
XY を算出する際、暗号鍵が0か1かによる処理の違いを少なくする方法として、モンゴメリラダー法を紹介します。
モンゴメリラダー法では掛け算と2乗算を行うモジュールを用意して暗号鍵の違いによらず常に動作させます。暗号鍵によって異なる処理は2乗算の入力を前回の掛け算結果にするか2乗算結果にするかの選択のみです。
図5はモンゴメリラダー法によって 310 を求めるときの動作です。暗号鍵になる指数部を2進数で表して上位から順に処理を行います。初期値を XY の X にあたる 「3」 と 「1」(1は固定値 ) に設定し、2進数で表した暗号鍵が1の時は前回の2乗算出力を、暗号鍵が0の時は掛け算出力を 次の2乗算に入力します。この手順に沿って順に処理を行うと、最終的に 310 を求めることができます。
モンゴメリラダー法を使用すると暗号鍵によらず同じ演算を繰り返す動作になり、電源にノイズとして漏れ出す消費電流の違いがありません。暗号鍵とリンクした情報が漏れ出さないため、サイドチャネル攻撃の対策とすることができます。
暗号だけがセキュリティではない
ここまで5回に渡ってデータを守るための暗号について解説をしてきましたが、攻撃者はさまざまな方法で攻撃を仕掛けてくるため、暗号だけでシステムを守ることはできません。最後に暗号だけでは防ぐことができない攻撃の例を挙げて、セキュリティはシステムとしての設計が大切であることに触れておきます。
再生攻撃 (リピート攻撃)
暗号鍵を盗み出して暗号データを解読するという試みを一切行わない攻撃に再生攻撃 (リピート攻撃) があります。
図6は再生攻撃の例です。攻撃者は、通信データを盗聴して盗み出し、盗んだデータをそのまま送信します。図の例では、同じデータを複数回送信することで機器を暴走させたり、正規のデータ通信を妨害することを狙った攻撃です。
また、図のような連続再生以外にも盗聴したデータを任意のタイミングで送信してシステムを誤作動させるような攻撃もあります。
再生攻撃では、暗号鍵を盗み出して暗号化されたデータを解読する必要がなく、データが暗号化されていること自体も攻撃者は意識する必要がありません。つまり、データの暗号化だけで再生攻撃を防ぐことはできません。
通信データを暗号化することでデータの漏洩を防いだり、改竄を検知することはできますが、攻撃者は手あたり次第通信データを盗み取り、適当なタイミングで適当なデータを送ってくるかもしれません。たまたまそのデータが機器の停止命令であれば、受信した機器のみが停止してシステムとして重大な誤作動に繋がるかもしれません。
再生攻撃は、データの中に必ず変化する部分 (通信ごとに +1 するパケット番号など) を組み込んでおき、同一なデータ (パケット番号が +1 されていないデータ) を受信した場合には不正なデータとして検出するような仕組みを組み込むことで防ぐことができます。
そして、パケット番号が改ざんされることを防ぐ方法として暗号化が有効な手段になります。
このように、暗号化は安全なシステムを構築するひとつの手段・道具であり、どういったエラー検出を組み込むか、エラーが発生したときの処理をどうするかといった全体を見通したシステム作りがシステムの安全に大きく関わってきます。
FPGAと暗号
本シリーズでは、「FPGA で作る暗号は危険 ?」と題して主にサイドチャネル攻撃の脅威を解説してきました。
FPGA は多様な機能要求に対して柔軟に対応できる便利なデバイスですが、サイドチャネル攻撃という脅威があることを意識せず、必要な対策を施していない暗号機能は非常に脆弱で危険なものになってしまうということを解説しました。
ひとつ勘違いをしないで頂きたいのですが、「FPGA で作る暗号は危険 ?」としているため、FPGA を使用した暗号機能が危険なように思われるかもしれませんが、サイドチャネル攻撃の脅威は FPGA のみにあるのではなく、ソフトウェアで実装した場合も同じです。逆に、ちゃんとした対策を組み込むことでソフトウェアよりも強固なサイドチャネル攻撃対策を FPGA では施すことができます。
また、サイドチャネル攻撃という攻撃方法があることを知っておくだけでシステムとしての安全性を高めることができます。
例えば、エラーを検出した場合に一旦電源を切るまで復帰できなくすることで AES 暗号にサイドチャネル攻撃を行うために必要な波形取得の時間が非常に長くなり、ひとつの防御策とすることができます。今回の記事がこういった対策を講じるための助けになれば幸いです。
ハードウェアセキュリティ
サイバーセキュリティという言葉のように、一般的にセキュリティといえばハッキングやウィルスを指すことが多いと思います。
しかし、IoT として通信によって接続される機器が増えるにつれて、ハードウェア面のセキュリティを高めることが重要になっています。重要な情報を守るため、是非、ハードウェアセキュリティという面も考慮に入れて頂ければと思います。
柔軟な機能が実現可能な面に注目されがちな FPGA にハードウェアセキュリティを組み込むことは製品の差別化としても有効な手段になるのではないでしょうか。
最後に
最後に少しだけ宣伝させて下さい。ゴフェルテックは、産業機器向けの受託開発を行っており、FPGA を使用した機器開発も多く手掛けています。暗号機能を初めとするセキュリティ関連技術は通信データの保護のみでなく、製品内部にある設計情報の漏洩・盗み出し防止にも活用でき、産業機器分野でもセキュリティが重要になると考えて研究・開発を行っています。FPGA を中心としたハードウェアセキュリティ関連で困ったことなどがありましたが、お気軽にご相談ください。
また、2021年1月20日から東京ビックサイトで開催されるオートモーティブワールドに出展する予定ですので、お越しの際は是非お立ち寄りください。
追記 (2021/1/15) :緊急事態宣言の発令を受けて、オートモーティブワールドへの出展を見合わせました。ご来場を予定されていた方には申し訳ありません。お問い合わせやご相談についてはゴフェルテックまでご連絡を頂けますようお願い致します。
株式会社ゴフェルテック 川西紀昭