FPGA 向けの真性乱数生成器 (TRNG) の設計法に関するコースも今回が最終回です.今回も、SR ラッチを禁止状態から保持状態へと移行させた時の挙動 (メタスタビリティ) を利用した TRNG を扱います。前回と異なるのは、最終的な出力ではなくメタスタビリティが解消されるまでの時間 (発振の回数) に注目する点です。
なお、この記事で紹介する TC-TERO (Three-path Configurable TERO) 型 TRNG に関する論文 [1] は、FPGA 関連の世界最大級の国際会議の1つである FPL において、私が今年 (2020年) 発表したものです。
TERO (遷移効果リングオシレータ)
TERO の動作原理
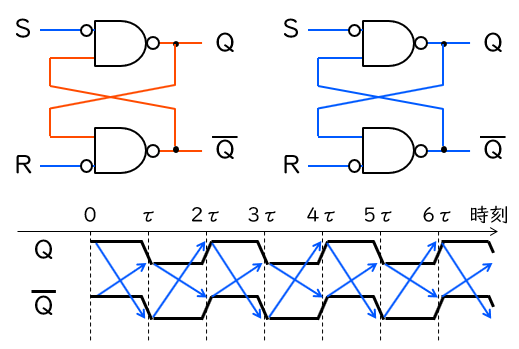
TERO (遷移効果リングオシレータ) は、論理的には前回紹介した SR ラッチと等価な回路です。SR ラッチにおいて、禁止状態から保持状態に切り替えたときのタイミングチャートを、下に再掲します。
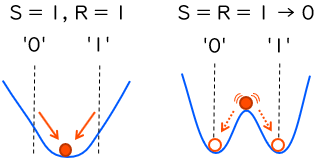
SR ラッチの S、R 入力を全く同時に ‘1’ から ‘0’ に切り替えると、理論上は永久に発振するものの、実際にはそのうち ‘0’ か ‘1’ かのどちらかに寄っていき、収束することを説明しました。またこれは、下図に再掲するように、ちょうど山の頂上にボールが乗っかっている状態にたとえられることも説明しました。
前回は、このボールを頑張って山の頂上にぴったり乗せることを考えてきたわけですが、それとは別に、意図的に山の頂上を ‘0’ と ‘1’ の中間からズレた位置に持っていくことも考えられます。この場合、ボールが転がり落ちる先は山の頂上をどちらにずらしたかによって固定されますが、ボールが転がり落ちるまでの時間には、依然として不確定性があります。この不確定性を利用するのが TERO 型 TRNG の考え方です。
具体的には、SR ラッチの上下の NAND ゲートの伝搬遅延に差をつけることで、発振が始まった時点での出力 Q の ‘0’ と ‘1’ の比率 (デューティ比) に差をつけることを考えます。この比率の差をここでは Δr とおきます。例えば ‘0’ が 45 %、’1′ が 55 % の時間だけ出現した場合、Δr = | 0.45 – 0.55 | = 0.10 です。
また、信号が8の字を1周するたびに Δr は増幅されるのですが、ここではその増幅率を R (1周するたびに Δr は R 倍になる) とします。つまり k 周の発振のあと、比率の差は理想的には Δr・Rk になります。これが 1 以上になったとき、比率は 0 % と 100 % となり、発振は止まることになります。
実際にはこれに熱雑音などの要因によるジッタが加わるため、もう少し式は複雑になります。詳細は本記事では省きますが、重要なことは、発振の回数の分布がこの Δr、R、それにジッタの相対値 σr によってモデル化できる[2] ということです。これにより、最終的に得られる乱数に偏りがないことを数学的に示すことができます。
これらのパラメータは、実際に TERO を構成して得られた発振の回数の分布から求められます。そして、モデルから得られた分布は、実際に得られた分布とよく一致します。例えば、本記事で紹介する提案手法である TC-TERO に対して行った検証では、Δr = 0.1159、R = 1.01908、σr = 0.00192 というパラメータが得られました [1]。なお、このときの発振回数の中央値は、114回でした (現に、Δr・R114 ≒ 1 であることが確認できます)。
TERO の設計におけるポイント
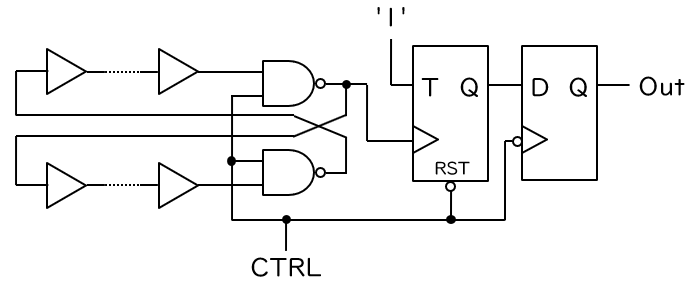
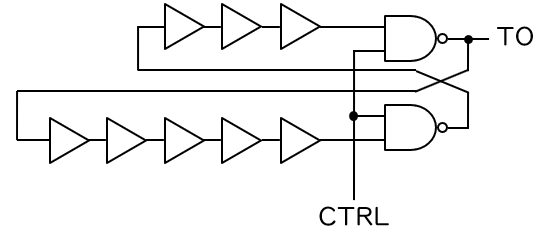
これで、TERO でメタステーブル状態が解消されるとき、発振の回数には不確定性があり、予測不可能であることがわかりました。この発振の回数が偶数であるか奇数であるかを T フリップフロップ (T-FF) を用いて判定することで、下図に示す TERO 型 TRNG が構成できます。ここでは、実質的に NAND ゲートの伝搬遅延を増加させるために、それぞれの NAND ゲートの前段に何個かのバッファを設けています (FPGA では、出力 = 入力である1入力 LUT を使います)。
ただこの TERO について、FPGA 向きの設計で先に紹介したモデルを考慮した事例は見当たりませんでした。そのため、まずはバッファの個数をどうするのが適切であるかを検討しました。先のモデルが示唆することは、以下のとおりです。
- Δr があまりに小さいと、発振の回数が大きくなりすぎる。最悪の場合は永久に発振する可能性もある。
- σr は相対値なので、8の字を1周する間の伝搬遅延の合計、つまりバッファの数が少ないほど大きくなる。
前者を考慮すると、上下のバッファの個数をあえて異なる値にして、Δr がほどほどの値になることを狙ったほうがよいことになります。もちろん、Δr が逆に大きすぎるとすぐに発振が止まってしまうため、適当なバランスを見つけ出す必要があります。
また、発振回数が一定値を超えるか、または一定時間が経過したときに、発振回数の測定を打ち切ることも必要です。そうでなければ、乱数の生成速度が突然遅くなる、あるいは全く乱数が生成できなくなる可能性があります。そのため、T-FF を9ビットのカウンタで置き換え、その最上位ビットが ‘1’ となったとき (つまり発振回数が 256 回になったとき) には、測定を打ち切ることとします。発振の停止や測定の打ち切りを判定するために、簡単な制御回路を追加します。
また、後者を考慮すると、バッファの数はなるべく少ない方がよいことになります。しかしながら、あまりにもバッファの数が少なすぎると、先ほど置き換えたカウンタが非常に高い周波数で動作することになります。その結果、カウンタがタイミング制約を満たせず、誤動作してしまいます。これもやはりバランスが重要です。
以上を考慮して試行錯誤を重ねた結果、Arty A7 ボードを対象とした場合には、バッファの個数をそれぞれ3個・5個とするのが適切であると結論づけました。このときの TERO の SR ラッチに相当する部分を下図に示します。全てのバッファと NAND ゲートが同一の伝搬遅延をもつと仮定すれば、(上側に4個、下側に6個のゲートがあるので) Δr = | 0.4 – 0.6 | = 0.2 となります。
この構成で、FPGA 内に TERO を配置する場所を変えながら、カウンタ値の分布を測定してみました。すると、10ヶ所中2ヶ所でそれなりの分散をもつ分布が得られた一方で、6ヶ所では発振の回数が少なすぎて、ほぼ同じカウンタ値しか得られませんでした。また、残りの2ヶ所では発振の回数が多すぎて、測定が頻繁に打ち切られてしまいました。
第2回で TERO 型 TRNG は回路の調整が難しいのが欠点だと書きましたが、十分考慮した設計を行ってもなお、うまくいく場合といかない場合があるわけです。どこに TERO を配置してもうまくいくようにするには、更に工夫が必要です。
実現性の高い TERO 型 TRNGに向けて
コンフィグ可能なリングオシレータ
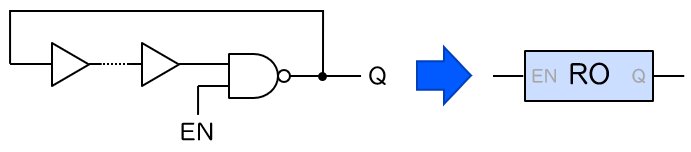
そこで目をつけたのが、COSO 型 TRNG の改良法として2019年の FPL で提案された、コンフィグ可能なリングオシレータ (Configurable Ring Oscillator、以下 C-RO と表記) です [3]。第2回でリングオシレータ (RO) を説明した際に、実際には下図に示す NAND ゲートと任意の個数のバッファからなる構成がよく用いられることを説明しました。
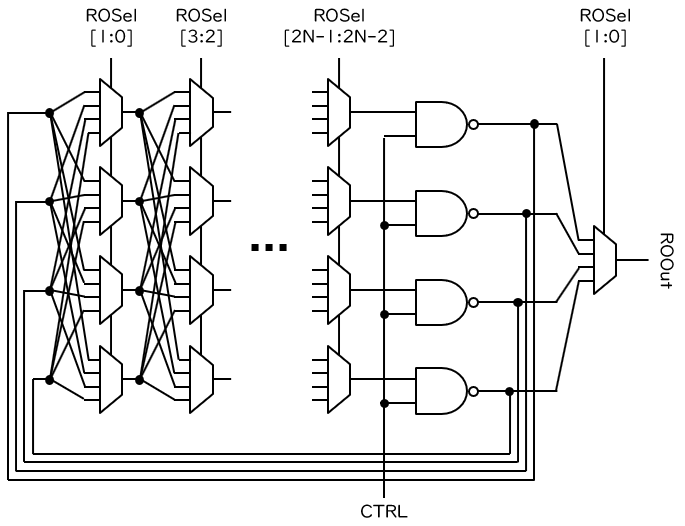
それに対して、C-RO は下図に示す構成をもちます。NAND ゲートとバッファの組を2組、あるいは4組コピーして、バッファの部分を2入力ないし4入力のマルチプレクサで置き換えます。図では4組コピーした場合を示します。
マルチプレクサのデータ入力には、その1つ前の段にある全てのマルチプレクサの出力を接続します。選択入力には、パラメータ ROSel の一部のビット (2入力なら1ビット、4入力なら2ビット) を接続します。これにより、元々のバッファの個数を N としたとき、パラメータ ROSel を切り替えることにより、この回路は 2N ないし 22N 通りの任意の経路を通れるようになります。
各マルチプレクサの伝搬遅延には、「製造時の特性のばらつき」によりわずかな差があります。そのため、通る経路が異なればリング1周分の伝搬遅延の合計も異なり、発振周期も異なります。COSO 型の TRNG では、周期が少しだけ異なる RO の組を見つけるのが難しいことが課題でした。しかし、C-RO を使い、パラメータを変えながら周期の比を調べていくことで、この問題が解決できたのです。
実のところ、この C-RO の構成を TERO 型 TRNG に応用する (以下これを C-TERO とします) だけで、TERO 型 TRNG の問題点である回路の調整の難しさも解決できてしまうことがわかりました。ただそれではあまりにも芸がない (論文としての新規性に乏しい) ので、もう少し工夫を重ねます。
省資源化に向けた工夫
そこで、前回示したスライスの内部構造を再考してみます。最近の Xilinx 社の FPGA では、LUT は単体で6入力1出力までの任意の論理関数を表現できますが、それに加えて、2個の LUT で7入力1出力の論理関数を実現するためのマルチプレクサが用意されているのでした。この2個の LUT の出力間をまたぐマルチプレクサを F7MUX とよびます。
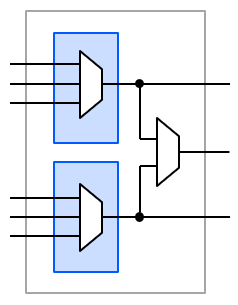
この F7MUX を使い、各 LUT を3入力のマルチプレクサとして動作するよう設定することで,下図に示す回路を構成します。3入力のマルチプレクサは、前段の回路の3つの出力のうちいずれかを選択するものとします。
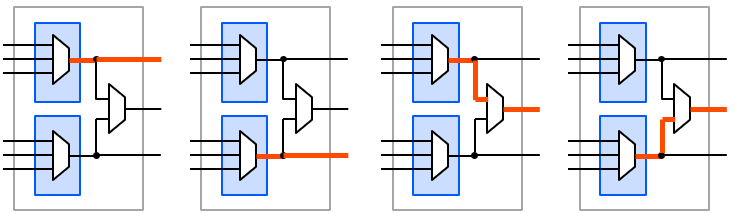
この回路から後段の回路までの経路として、下図に赤線で示す4つのパターンが考えられます。それぞれ、(1) 上側の LUT の出力をそのまま出力、(2) 下段の LUT の出力をそのまま出力、(3) 上段の LUT の出力を F7MUX で選択して出力、そして (4) 下段の LUT の出力を F7MUX で選択して出力、に対応します。
C-RO では、バッファあたり2ビットのパラメータを得るために、バッファと NAND ゲートの組を4組コピーする必要がありました。そのため、バッファあたり4個の LUT と、段と段との間に4本の配線が必要でした。一方この方法ならば、バッファあたりの LUT の数は2個、段と段との間の配線の本数は3本で済みます。この特徴から、私はこのコンフィグ可能なリングオシレータの構成方式を TC-RO (Three-path Configurable RO) と名づけました。
更に嬉しいことに、この方法であれば3入力マルチプレクサと NAND ゲートを1つの LUT にまとめられます。3入力マルチプレクサは3本のデータ入力と2本の選択入力を持ちますから、これに NAND ゲートの入力の1つを加えても、入力の本数の合計は6本で済むのです。
TC-TERO 型 TRNG
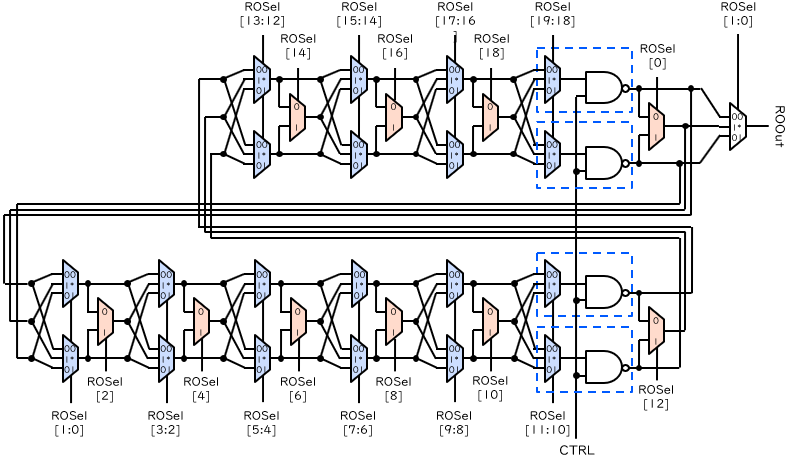
ここまでの話を総合して最終的に提案した、コンフィグ可能な TERO (TC-TERO) [1] の回路図を下図に示します。8の字の中のマルチプレクサのうち、LUT で作られるものは青、F7MUX で作られるものは赤で、それぞれ色付けしています。また点線の枠はその回路が1つの LUT にまとめられることを意味します。
この TC-TERO で作った TRNG を先行研究の C-TERO で作った TRNG と比較しました。取りうる全てのパラメータに対してカウンタ値の平均と分散を求めたところ、発振回数の平均が程よい (96~127) 値になるパラメータの割合がおおよそ2倍 (C-TERO では 2.62 % であったのに対して、TC-TERO では 5.18 %) になることがわかりました。特に、TERO を配置する場所によっては、より顕著な差が見られました。
私はこの結果を、スライス間の配線が TERO の特性に影響を与えており、より多くの論理素子・配線を使う C-TERO の方がその影響を大きく受けたからではないか、と分析しています。TRNG の回路をコンパクトにしておくというのは、単に他の回路に多くの論理素子を割けるというだけではなく、TRNG 自身への悪影響を避けるためにも有用であるようです。
また、この中から適当な1つのパラメータを選んでしばらく乱数を生成しつづけ、得られたビット列に簡単な後処理をしてから NIST の試験にかけたところ、試験に合格したことも確認しています。このときの乱数の生成速度は 1.912 Mbit/s でした。他の種類の TRNG と比べても、ハードウェアの使用量、生成速度ともに遜色ない結果です。
まとめ
今回は、TERO 型の TRNG についての紹介でした。今回もまた、FPGA の論理ブロックの内部構造の理解が、新たな回路構造の提案に役立った一例といえるかと思います。
このコースでは、第1回で TRNG に関する基礎知識を説明し、第2回で2016年時点で FPGA 向けの TRNG として有力な型をいくつか取り上げました。そして、第3回~第5回で、そのうちいくつかの型について、その原理の詳しい紹介と、我々がその改善のために取り組んできたことについて説明してきました。
第1回で TRNG の評価基準として回路⾯積、⽣成速度、ランダム性やそれを裏打ちする確率的モデルの有無、デバイスや環境への⾮依存性などを挙げました。2016年時点ではこれらを全て満たす FPGA 向けの TRNG を実現するのは困難でしたが、最近の改善によりそうした TRNG がいくつか登場したことになります。そういう意味で、FPGA 向けの TRNG の構成法そのものについての研究は、一段落つきつつあるのかもしれません。
しかし、こうした TRNG をいかに上手く使うか、考え方をどう応用するかについては、まだやるべきことが多く残されています。私の研究室でもまさに今そうした研究をいくつか進めているところです。このコースで紹介したことが、読者の皆さんの FPGA を用いた研究・開発へのインスピレーションの1つとなることを祈っています。
愛知⼯業⼤学 藤枝直輝
参考文献
- [1] N. Fujieda: On the feasibility of TERO-based true random number generator on Xilinx FPGAs, 30th International Conference on Field-Programmable Logic and Applications (FPL 2020), pp. 103–108, 2020. DOI: 10.1109/FPL50879.2020.00027
- [2] F. Bernard, P. Haddad, V. Fischer, and J. Nicolai: From Physical to Stochastic Modeling of a TERO-based TRNG, Journal of Cryptology, Vol. 32, No. 2, pp. 435–458, 2019. DOI: 10.1007/s00145-018-9291-2
- [3] A. Peetermans, V. Rožić, and I. Verbauwhede: A Highly-Portable True Random Number Generator based on Coherent Sampling, 29th International Conference on Field Programmable Logic and Applications (FPL 2019) pp. 218–224, 2019. DOI: 10.1109/FPL.2019.00041