FPGAを用いた「組合せ問題」の高速計算 (4)

前回は、Parital MaxSAT の発見的解法である Dist アルゴリズム[1]の FPGA 実装にあたっての難点を挙げ、アプリケーションを最大クリーク問題に特化することでそれらを回避できることを述べました。

今回は、その FPGA 実装[2]について述べていきます。

全体像

まず、前回示した最大クリーク問題専用 Dist アルゴリズムを図 1 に再掲します。

次に、データを保持するためのテーブル類を図 2 に示します。

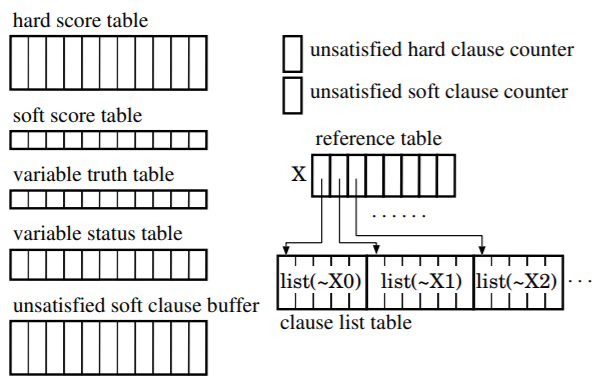
hard score table と soft score table は名前の通りで、各変数の hard score と soft score をそれぞれ保持するテーブル、variable truth table は変数の真理値を保持するテーブルです。

variable status table は、個々の変数が属している集合 (H、S、Us のうちどの集合に属しているか) を表すテーブルであり、図1のステップ4で使用されます。

unsatisfied soft clause buffer は、非充足な soft clause、すなわち集合 Us です。集合 H、S、Usのうち、その要素を明示的に持つのは Us だけです。 variable status table があるため、本当は Us も明示的に持たなくてもよいのですが、このようにした理由は後述します。

variable status table、 variable truth table、hard score table、soft score table は32個の sub-bank から構成されます。これは、図1のステップ6、7において、一度に最大32個の変数を並列に処理できるようにするためです (32 という数字は決め打ちです。基本的には大きければ大きいほど性能向上に寄与します) 。

unsatisfied hard clause counter と unsatisfied soft clause counter は、非充足な hard 節と非充足な soft 節の数を数えるカウンタであり、現在の解が実行可能解であるかどうかの判別と、実行可能解の質の評価に使用します。実行可能解の意味は前回の記事をご覧ください。

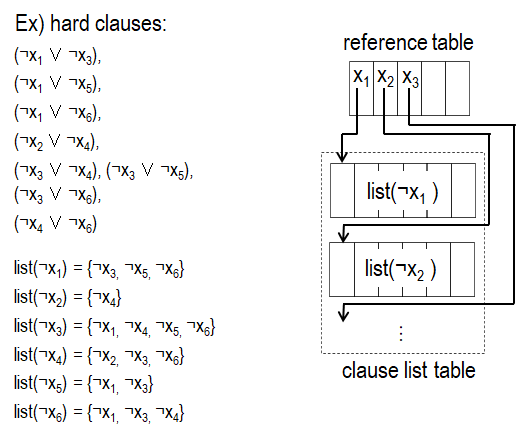
list table は、変数 x に対する list(x) を保持するテーブルです。ここで list(x) は、変数 x がフリップされた際に、hard score の再計算が必要となる変数のリストで、変数 x と同じ hard 節に含まれている変数がこれに該当します。reference table は、変数 x を list(x) の先頭アドレスに変換するためのアドレス変換表です。

図3 に list table の例を示します。

以上のテーブル類は、FPGA が搭載されているホスト PC 上で初期化され、FPGA にダウンロードされます。

解探索の実装

この節では、図1 のステップ 4 ～ 7 のハードウェア実装について述べていきます。

ステップ4

ステップ4では、フリップされる変数 xf の選択を行います。まず、集合 H、S、Us のいずれかを、優先度 H > S > Us で選択し (H ≠ ∅ なら H を選択、 H =∅ かつ S ≠ ∅ なら S を選択、H も S も ∅ なら Us を選択) 、続いて、選んだ集合の中から変数をランダム選択します。

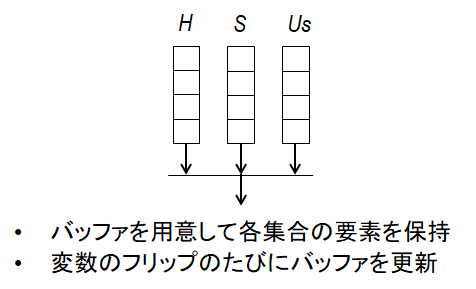
まず考えられるのは、図4のように、集合 H、S、Us の要素をそれぞれバッファに保持しておき、上記の優先度に従ってバッファを選択したうえで、そのバッファの中から変数をランダム選択する、というものです。この方法では、処理時間 O(1) で xf を決定できますが、次のような難点があります。

前回の記事でも述べましたが、変数のフリップの度に、最大で数1000 程度の変数の hard score が変化します。したがって、変数のフリップのたびに、最大で数1000程度の変数が集合 H、S を出入りします。所属先となる集合が変わる変数がバッファ内のどこにあるかはわからないため、それらを過不足なく拾い出すには、バッファ内を逐次的に探索する必要があり、FPGA で処理する際のボトルネックとなってしまいます。

なお、集合 Us を出入りする要素は一度にひとつであり、上述の問題は発生しません。

variable status table を用いた xf の選択

そこで、この実装では、集合 H、S、Us を明示的に持つ代わりに、以下のようにしました。

まず、ある変数 x がどの集合に所属しているかを3ビットの2進数で表します。このとき、割り当てられた2進数が集合 H、S、Us の順に大きくなるようにします(つまり、選択の優先度の高い集合へより大きい値を割り当てる)。

続いて、各変数の status をテーブル化します。これは図2の variable status table に該当します。

以後、変数 x の status を status(x) と表記します。

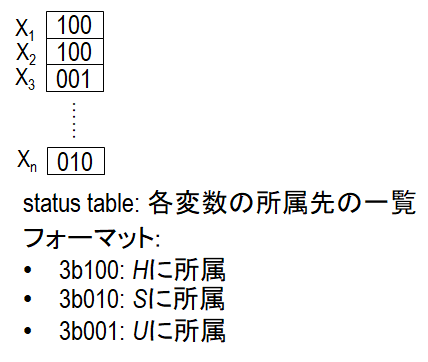
図5に variable status table の概略を示します。矩形の中の数字は、その左の変数の status、つまり、所属する集合を表します。今回の実装では、100 が集合 H、010 が集合S、 001 が集合 Usを表しています。テーブルを変数番号で引けば、その変数がどの集合の要素であるかがわかります。

以上のようにすることで、ステップ4は、

• (a) variable status table 内の全ての status を比較して、その中から最大値を選ぶ (最大値が複数ある場合はその中からランダムに選択する)

という処理に置き換えることができます。

この手法では、図4の方式と比べると、xf の決定にかかるステップ数は増えますが、集合間の移動が status のアップデートで実現されるため、図4の方式のように各バッファの中身を逐次的に走査する必要がなくなります。

また、status を複数の sub-bank に分けて持っておけば、status の読み出しや更新が並列に行えます。また、これにより、statusの大小比較をリダクション演算化できるため、 xf の選択もそれほど低速にならずに実行できます。

図7に、変数 xf の選択をリダクション演算で実行するための回路を示します (以降、 reduction tree と表記) 。

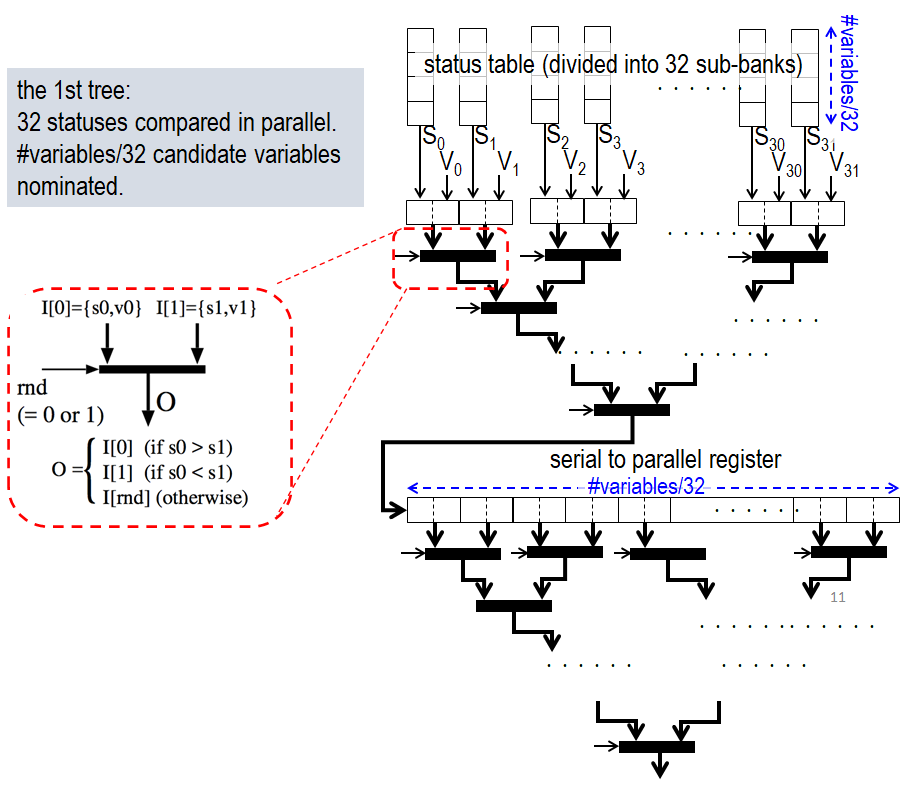
赤い点線で囲まれているのはマルチプレクサで、status と変数の組が 2つ入力され、 それらのうち status の大きい方を選択 (status が等しい場合は乱択) して出力します。このマルチプレクサを2分木状につなげることで、status の最も大きい変数を選択できるようになります。

reduction tree の性能は、理想的には O(log Nv) (ここで Nv は変数の総数) ですが、実際には status table から一度に読み出し可能な値の数により制限されます。

今回の実装では status table を32個の sub-bank に分けて保持しているため、一度に比較可能な status の数は最大32です。まず、図7の1段目の reduction tree を用いて、 変数の選択が Nv/32 回実行されます。これにより、 Nv/32 個の候補が選択され、図7の serial-to-parallel-register に格納されます。続いて、2段目の reduction tree を用いて、serial-to-parallel-register の中から変数がひとつ選択されます。

選択された変数の status が 100 または 010 であれば、この変数を xf とします。一方、statusが 001 の場合は、この変数を破棄し、図2の unsatisfied soft clause buffer の中から変数を乱択して、それを xf とします。

言い換えると、xf を集合 H または S から 選択する場合は variable status table と reduction tree を使用するが、集合 Us から選択する場合は unsatisfied soft clause buffer の中から乱択する、ということです。これは、このようにしないと性能低下 (解の精度が落ちる) が見られたためです。

その理由はまだわかっていませんが、 reduction tree を用いる方法では選択される変数に偏りが起こりやすく、集合 Us から xf を選択する場合には、その影響が無視できなくなるためではないかと考えています。

ステップ5

ステップ4で選択された変数 xf で variable truth table を引き、読み出された真理値の否定を取って variable truth table に書き戻します。

また、xf の新しい真理値に応じて unsatisfied soft clause counter を更新します (xf が非充足ならデクリメント、充足ならインクリメント) 。更に、xf が偽になった場合は，unsatisfied soft clause buffer に xf を追加します。

ステップ6、7

xf の hard score と soft score、 list(xf) に含まれる変数 x_i (i = 0 ～ |list(xf)| – 1)の hard scoreを更新します (ここで |list(xf)| は list(xf) の長さ) 。

以後、任意の変数 x の hard score と soft score をそれぞれ hscore(x) と sscore(x) で表します。

まず hscore(xf) と sscore(xf) ですが、これらは現在値の正負を反転させることで新しい値に更新されます。

hscore(x_i) は、フリップ後の xf の真理値と、x_i の現在の真理値に依存します。具体的には、hard score の定義から、図8のようになります。

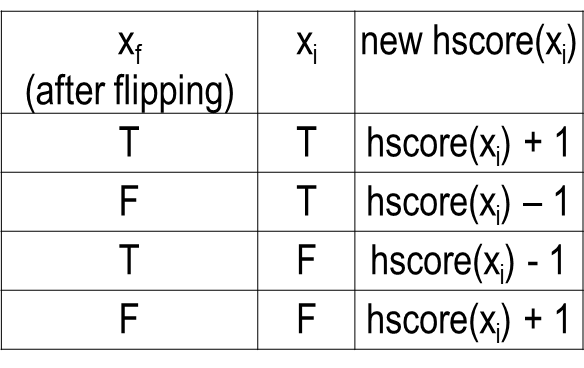
図9に hscore(x_i) と status(x_i) の更新を行う回路の概略を示します。

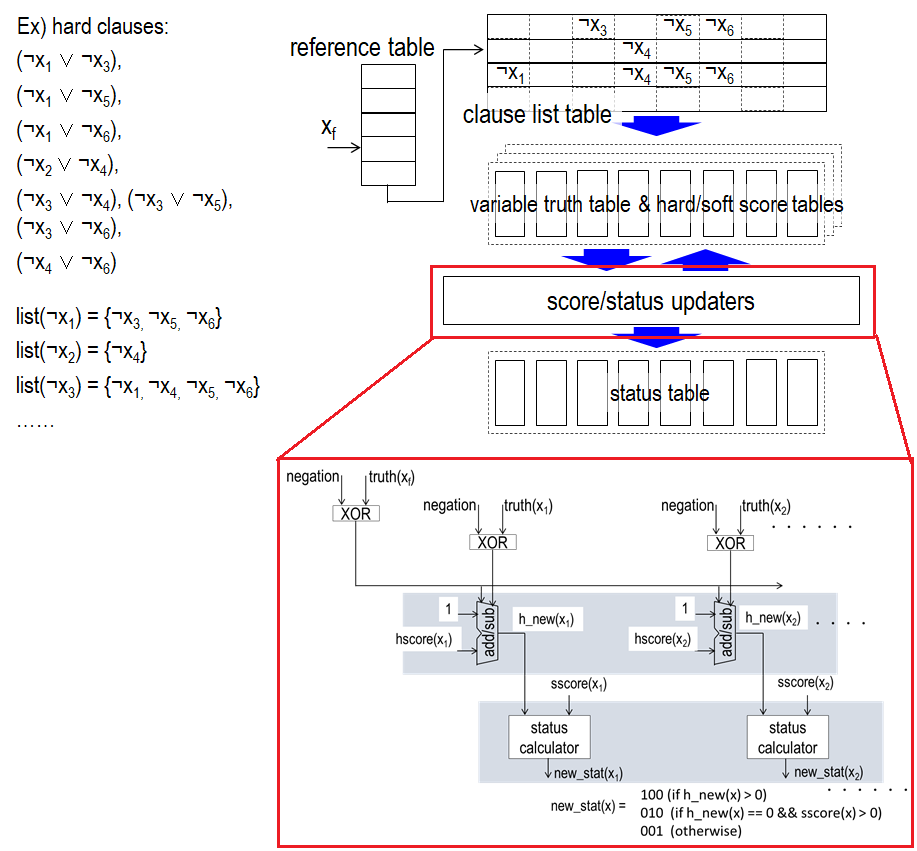
まず、(1) list(xf) から変数を最大32個ずつ読み出します。(2) 読み出された変数の真理値、hard score、 soft score を、variable truth table、hard score table、soft score table からそれぞれ読み出します。続いて、(3) 図8に示した演算規則に従って hard score をアップデートし、(4) hard score tableに書き戻します。また、充足された hard 節や非充足になった hard 節がある場合は、それに合わせて unsatisfied hard clause counter の値を増減させます。並行して、(5) 更新後の hard score と soft score に基づいて status を算出し、variable status table に書き戻します。

|list(xf)| が32を超える場合は、(1) ～ (5) を |list(xf)|/32 回に分けて実行します。この処理はパイプライン化が可能で、それにより、並列度は 32×パイプライン段数となります。

まとめ

今回は、最大クリーク問題に特化した Dist アルゴリズムのFPGA実装について述べました。

次回は、このハードウェアの性能と課題について述べたいと思います。

筑波大学　金澤 健治

参考文献

[1] Cai, S., Luo, C., Thornton, J., & Su, K, “Tailoring Local Search for Partial MaxSAT,” 28th AAAI,pp. 2623-2629, 2014.

[2] Kanazawa, K., & Cai, S., “FPGA acceleration to solve maximum clique problems encoded into partial MaxSAT,” IEEE 12th International Symposium on Embedded Multicore/Many-core Systems-on-Chip, pp. 217-224, 2018.