本連載もいよいよ最終回。デルタシグマ変調も正弦波生成もできるようになりましたので、いよいよ FPGA ピアノを完成させます。異なる周波数で発振する複数の正弦波生成モジュールを並べ、複数の音を同時に出力できるようにします。つまり和音の演奏を可能にします。さらに BRAM を用いた ROM テーブルに楽曲のデータを保存しておき、それを読み出しながら自動演奏する機能も実装し、最後は本連載の「卒業演奏」に臨みます。
まずは鍵盤に見立てたスイッチボタンと正弦波の生成を連携させるために、前回の設計を少し手直しするところから始めます。
正弦波生成をスイッチボタンと連携させる
不連続信号の除去
前回実装したテスト回路も、スイッチボタンを押すと音が鳴るというものでした。しかし、前回の正弦波生成モジュール (sine_wave_generator) はボタン入力とは無関係に動作させていたため、発音の開始と停止の部分で出力信号が不連続になっていました。シミュレーション波形を見るとよく分かると思います。
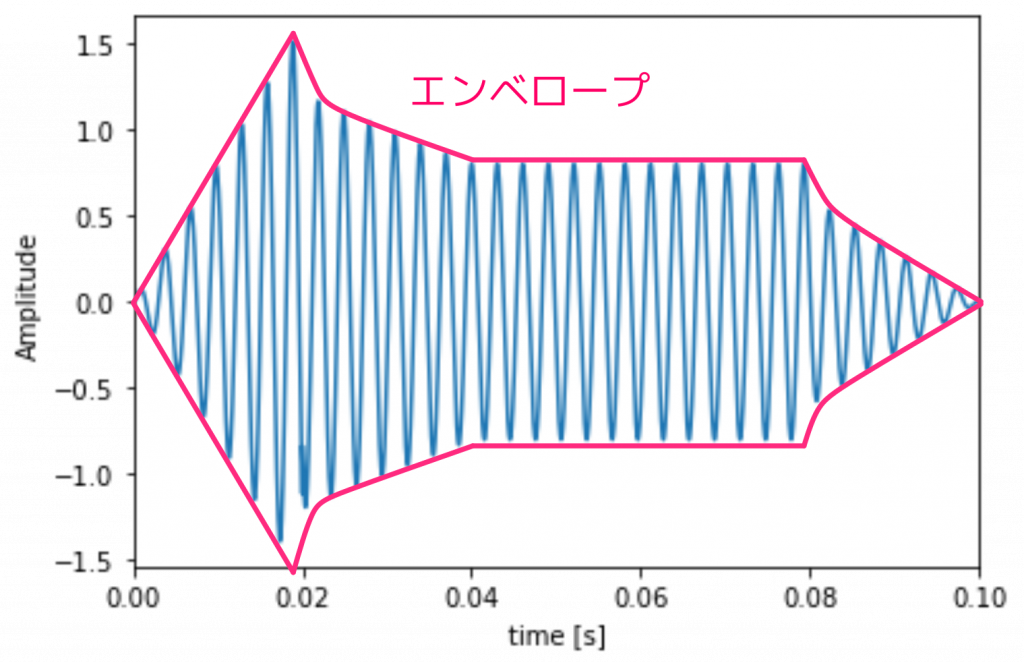
この部分では「プスッ」というノイズが発生するため、電子楽器としては耳障りです。それではどうするのかということですが、一般的なシンセサイザー (論理合成ではなく、電子楽器の方です!) では、そもそもこのような問題は生じません。というのは、シンセサイザーは振幅のエンベロープ (包絡線) もデザインするようになっており、典型的には次の図のような波になるからです。
このため音の出だしや切り際で出力信号が不連続になりません。これを実現するには、正弦波の出力とエンベロープの波形を乗算すれば良いのですが、今回は手を抜いて振幅はいじらないことにします。
その代わりに、スイッチボタンを離してもすぐに音を止めずに、出力信号の値がゼロになるまで待ってから正弦波の生成を止めることにします。といっても、漸化式による計算では出力値がぴったりゼロになるとは限らないので、出力値がゼロをクロスしたら (符号が変わったら) 止めることにします。もちろん、スイッチボタンが押されて音を出し始める際には、出力値ゼロから正弦波生成を開始するようにします。
発振・停止の状態遷移
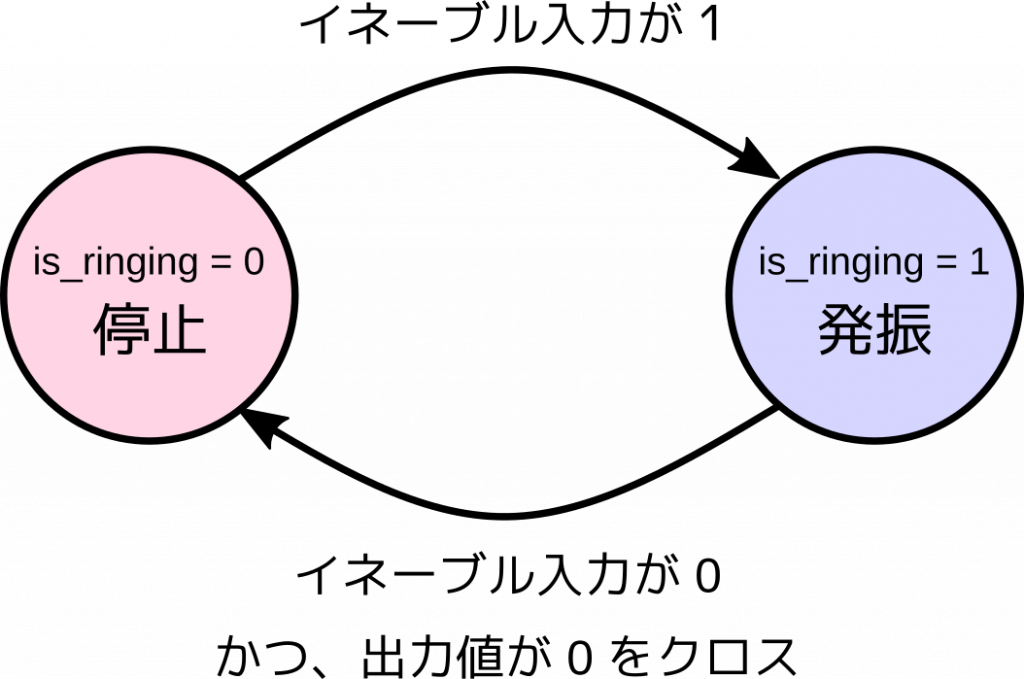
正弦波の発振をスイッチボタンと連動させるために、sine_wave_generator モジュールにイネーブル入力を追加します。これに1が入力されると発振を開始します。これに0が入力されたら発振を停止しますが、すぐに停止するのではなく、出力値が0をクロスするまで待ってから停止します。
これを実現するために、sine_wave_generator モジュールの内部に、停止と発振の状態を管理する1ビットの状態レジスタ is_ringing を設けます。状態遷移図は次のようになります。
簡単ですね。これを SystemVerilog で書くと次のようになります。
// 発振開始・停止の状態制御
always @(posedge clk) begin
if (!is_ringing && en_in)
is_ringing <= 1'b1;
else if (!en_in && zero_crossed)
is_ringing <= 1'b0;
endここで、en_in はイネーブル入力、zero_crossed は出力値ゼロクロスの検出フラグです。
ゼロクロスの検出
出力値のゼロクロスを検出するのは難しくありません。1つ前のクロックにおける出力値の符号ビット (MSB) を1ビットのレジスタに保存しておき、今の出力値の符号ビットと比較すれば良いのです。この比較が一致しなければ、出力値がゼロをクロスしたことがわかります。SytemVerilog の記述例を示します。
// 1クロック前の符号を保存しゼロクロスを検出
always @(posedge clk) begin
previous_sign <= dout[WIDTH-1];
end
assign zero_crossed = (dout[WIDTH-1] != previous_sign);ここで dout は幅が WIDTH ビットの出力値、previous_sign は直前のクロックにおける出力値の符号を保存する1ビットのレジスタです。
漸化式計算の制御
ステートマシンができましたので、リープフロッグによる漸化式の計算を is_ringing が1のときだけ行うように変更します。また、必ず正弦波の発振が0から始まるように、is_ringing が0のときに、freg と greg の値を初期化するようにします。
// レジスタ更新
always @(posedge clk) begin
if (!is_ringing) begin
freg <= '0;
greg <= G0 * (2.0 ** (WIDTH-1));
end
else begin
if (!turn)
freg <= freg + kterm;
else
greg <= greg - kterm;
end
endsine_wave_generator モジュールの主な変更点は以上です。完全なファイルは Gist にありますので、ご確認ください。
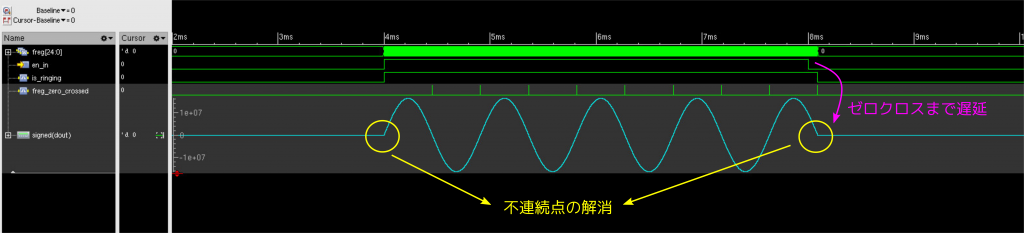
シミュレーションの結果は次のとおりです。期待したように、正弦波の発振が0で始まり、0で終わっていることが分かります。イネーブル入力が0に落ちてから、発振が止まるまで少しタイムラグが生じますが、今回は「余韻」と考えて気にしないことにしましょう。
電子楽器の処理としては異例かもしれませんが、交流信号のゼロクロス時にスイッチングを行うというのは、パワーエレクトロニクスなどの分野ではしばしば見られる処理のひとつです。
ピアノモジュール
これで部品は揃いました。いよいよピアノモジュールの設計です。まずは異なる高さの音を出すプローチについて考えます。
振動体の単複
楽器は音を出すために何かを振動させます。音の高さを変えるには、振動の周波数を変えなければなりません。このとき、2つのやり方が考えられます。
- 振動体そのものの振動周波数を変える
- 別の周波数で振動する振動体を並べる
小学校の音楽の授業でお馴染みのリコーダーは1の方式です。リコーダーを吹くと筒の中の空気 (気柱) が振動するわけですが、指で穴を塞ぐことによってその振動の周波数が変わり、音の高さが変わります。このような楽器では、一度に1つの音しか出すことができません。
対してピアノは2の方式です。88個のキーひとつひとつに対して、その音の周波数で振動する弦が用意されています (実際には1つの音に対して複数の弦が張られています) 。弦の周波数は固定されており、演奏中には変更できません。異なる高さの音は、異なる弦が振動することによって出されます。したがって、異なる高さの音を同時に出すことが可能になります。
バイオリンは1と2のハイブリッド方式ですが、弦の数は高々4本ですので1の要素が強いといえます。
FPGA ピアノにおいて弦に対応するのは、さきほどの正弦波生成モジュール sine_wave_generator です。このモジュールを1つだけ使用し、正弦波の周波数を動的に変化させて音の高さを変えるというアプローチは、さきほどの1の方式に対応します。しかし、それでは和音を出すことができません。やはりピアノというからには、和音を出したいところです。そこで、sine_wave_generator モジュールを音の数だけ並べて、2の方式で設計することにします。
全体の構成
sine_wave_generator モジュールはパラメータによって発振周波数を設定できるようになっています。それを音階の周波数に対応させ、音の数だけ配置し、それぞれのイネーブル信号にスイッチボタンを接続すれば良さそうです。しかし、Arty も含めて多くの FPGA ボードはスイッチボタンがせいぜい数個しかありませんので、幅広い音域の演奏を愉しむことはできません。
そこで、イネーブル信号を自動で生成する自動演奏モジュールも作ることにします。自動演奏といっても、あらかじめ ROM (Read Only Memory) に書き込んでおいたデータを順々に読み出して出力するだけです。ちょうどオルゴールのシリンダのようなイメージです。
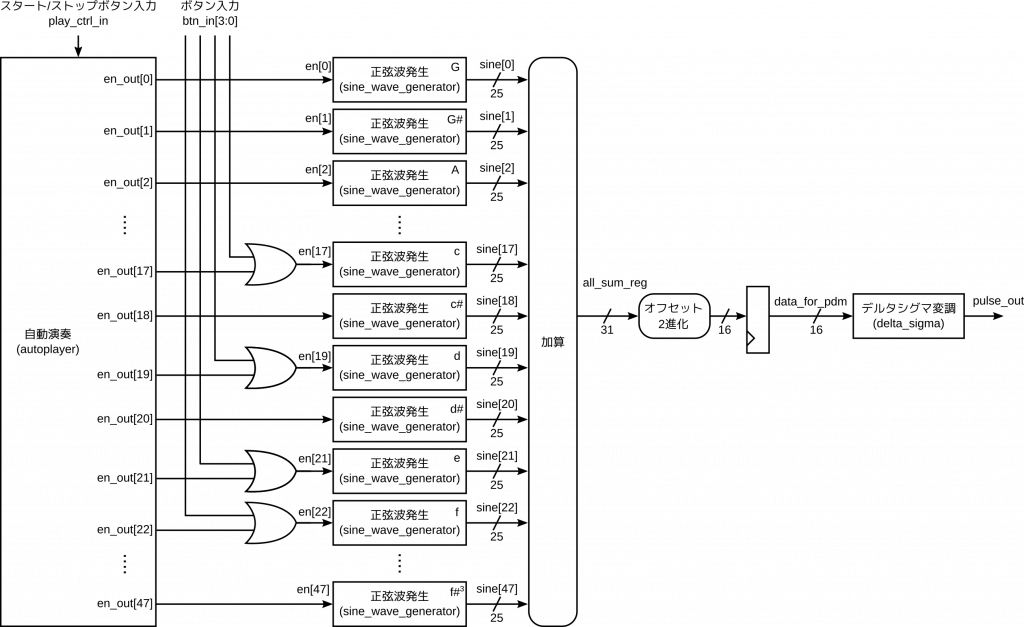
これらを構成図としてまとめると次のようになります。
本物のピアノではキーの数は88ですが、今回は48としました。特に深い理由はなく、適当に決めた数です。音域も適当に定めて、最低音を G 音 (基準音の2オクターヴ下の「ラ」のさらに全音下の「ソ」の音)、最高音を f#3 音 (基準音の2オクターヴ上の「ラ」の短3度下の「ファ♯」の音) としました。Arty の4つのボタンスイッチは、これまでと同じように、中央のド (c音)、レ (d 音)、ミ (e 音)、ファ (f 音) に対応させることにします。
ボタンスイッチの入力信号と、自動演奏モジュールの出力とは OR をとるようにします。つまり、自動演奏にあわせて、スイッチボタンを押すことで合奏 (?) もできるような構成です。
48個の正弦波発生モジュールの出力値はすべて合算し、最終的な出力波形の数値を得ます。その後はこれまでと同様の処理となります。すなわち、2の補数表現をオフセットつきの2進数に変換し、その上位16ビットをデルタシグマ変調します。その結果得られた1ビットのパルス信号が最終的な出力となります。
正弦波生成モジュールの並置記述
正弦波発生モジュールを48個並べる記述例を示します。generate for の省略記法を用いていますが、ツールによっては対応していない場合もあるかもしれません。その場合は、第1回のトップモジュールの説明を参考に、保守的な記述に書き直して下さい。
// 正弦波生成
for (genvar i = 0; i < NKEYS; i++) begin
sine_wave_generator
#(
.CLK_FREQ(CLK_FREQ),
.WIDTH(SINE_WIDTH),
.K_WIDTH(SINE_K_WIDTH),
.TARGET_FREQ(n2freq(i - 26)), // 周波数の指定
.AMP(SINE_AMP)
)
sine_wave_generator_inst
(
.clk(clk),
.en_in(en[i]),
.dout(sine[i])
);
endNKEYS が音の数のパラメータで、48に設定しています。周波数のパラメータ TARGET_FREQ の設定に出てくる -26 という数値は、今回の最低音である G 音が基準音 (a1 音) から低い方に半音距離で26だけ離れていることに由来します。ここで使っている関数 n2freq は基準音からの距離に基づいて周波数を計算するものです。
// 基準音の距離から周波数を計算する関数
function real n2freq(int n);
return ((2.0 ** (n / 12.0)) * BASE_FREQ);
endfunction自動演奏モジュールが出力する48ビットのイネーブル出力 autoplayer_out と、4ビットのボタン入力 btn_in の OR は、ノンブロッキング代入を使って次のように記述できます。
// ボタン入力に対応させる鍵盤の番号
localparam bit [$clog2(NKEYS)-1:0] BUTTON_NO[NBUTTONS] = '{
22, 21, 19, 17 // ファ,ミ,レ,ド
};
...
always_comb begin // 自動演奏によるイネーブルとボタン入力の論理和
en = autoplayer_out;
for (int i = 0; i < NBUTTONS; i++)
en |= btn_in[i] << BUTTON_NO[i];
endどのボタンがイネーブル信号の何ビット目に対応するのかを、あらかじめ定数配列 BUTTN_NO に設定しておき、OR をとる際のシフト量としています。
たかが加算、されど加算
さて、48個の正弦波出力を加算する必要がありますが、さすがに1クロックで一気に足すのは無理があります。そこでパイプライン型の加算器のツリーを作って足すことにします。
正弦波生成モジュールの出力データは25ビットですので、Arty を100 MHz で動かす場合、1クロックで4個程度なら無理なく加算することができます。そこで、48個のデータを4進木の形状で足すことにします。すると木の高さは、\[
\left\lceil \log_4 48 \right\rceil = 3
\]となります。つまり48個のデータの総和を3クロックかけて求めることになります。
この構造の一部を図示すると次のようになります。結構、大掛かりなハードウェアとなります。
完全にパイプライン化されており、新しい計算を1クロックごとに開始することができます。つまり、イニシエーションインターバル (II) が1のパイプラインです。
また、オーバーフローが生じないように、木のレベルを1段進むごとに、データ幅を2ビットずつ広げる必要がある点にも注意が必要です。具体的には、レベル1 (L1) では、27ビットのパイプラインレジスタが12個、レベル2 (L2) では29ビットのパイプラインレジスタが4個必要になり、際終段のレジスタ (all_sum_reg) のビット幅は31ビットとなります。
和音を出すだけなのに、ここまで気合の入った (?) ハードウェアを投入するべきかはちょっと微妙なところです。レイテンシをもう少し延ばしたり、重ねることのできる音の最大数に上限を設けたりすることでもう少しコンパクトにする手もあると思います。
もうひとつの問題は、オーバーフローしないように加算結果の幅を6ビット増やしたことにより、単音の振幅は64分の1に小さくなるという点です。それでも聴こえなくわけではないのですが、かなり小さな音になりますし、SN 比の面でも不利になります。実際にすべての音を同時に鳴らすということはほとんどないと考えられますので、出力レベルのレンジに何らかの調整機能を持たせるのが良いと思います。このあたりは工夫してみてください。
それではツリー加算の記述例を示します。構造をイメージしやすいように、各レベルごとに書いています。また、最終段は3つのレジスタの値を足すだけなので、ループを使わずに直接書き下しています。
// パイプライン型ツリー加算器
localparam int N_ARY = 4; // 木の基数
localparam int N_L1 = $ceil(real'(NKEYS) / N_ARY); // L1 のノード数
localparam int N_L2 = $ceil(real'(N_L1) / N_ARY); // L2 のノード数
// L1 の加算
logic signed [(SINE_WIDTH+2)-1:0] lv1_sum[N_L1];
always_comb begin
for (int i = 0; i < NKEYS; i += N_ARY) begin
lv1_sum[i / N_ARY] = '0;
for (int j = 0; j < N_ARY && (i + j) < NKEYS; j++)
lv1_sum[i / N_ARY] += sine[i + j];
end
end
// L2 の加算
logic signed [(SINE_WIDTH+4)-1:0] lv2_sum[N_L2];
always_comb begin
for (int i = 0; i < N_L1; i += N_ARY) begin
lv2_sum[i / N_ARY] = '0;
for (int j = 0; j < N_ARY && (i + j) < N_L1; j++)
lv2_sum[i / N_ARY] += lv1_sum_reg[i + j];
end
end
// ツリー加算のパイプラインレジスタ
logic signed [(SINE_WIDTH+2)-1:0] lv1_sum_reg[N_L1] = '{default: '0};
logic signed [(SINE_WIDTH+4)-1:0] lv2_sum_reg[N_L2] = '{default: '0};
logic signed [(SINE_WIDTH+6)-1:0] all_sum_reg = '0;
always @(posedge clk) begin
lv1_sum_reg <= lv1_sum;
lv2_sum_reg <= lv2_sum;
all_sum_reg <= lv2_sum_reg[0] + lv2_sum_reg[1] + lv2_sum_reg[2];
endもちろん、レベル方向にもループ記述を用いることで完全にパラメタライズすることも可能です。コンパクトな記述になりますので、挑戦してみるのも面白いでしょう。
自動演奏モジュール
基本構成
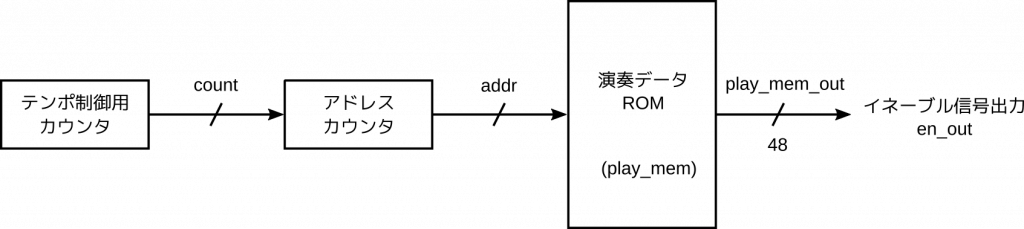
自動演奏といっても、あらかじめ ROM に書き込んでおいた48ビットのイネーブル信号を順に読み出すだけですから、ハードウェアとしては簡単です。基本的な構成図は次のとおりです。
ROM に書き込んでおくのは1ワード48ビットの演奏データです。つまり1拍ごとに、鳴らす音を1、鳴らさない音を0としたイネーブル信号のデータを作っておくのです。ワードの総数がその楽曲の拍数ということになります。
アドレスカウンタは ROM から読み出す番地を保持します。読み出す番地は1つずつ進めていけばよいのですが、1クロックが1拍ではないので、もうひとつテンポ制御用のカウンタを用意し、1拍に相当するクロック数をカウントします。このようにして演奏速度に合わせて演奏データを読み出していきます。
BRAM による ROM テーブルの実装
ここに来て、この連載初登場となるのが ROM テーブルです。今回は FPGA 内部のメモリ資源である Block RAM (BRAM) を使ってみることにします。BRAM の詳細については、BRAM 達人への道や FPGA をもっと活用するために IP コアを使ってみよう (4) が大変参考になりますので、ぜひご覧ください。
BRAM を使う方法にもいろいろありますが、ここでは SystemVerilog の記述から推論させる方式をとります。また、別途用意したテキストファイルからシステムタスク $readmemh を使って初期値を設定します。特別なツールを使わなくても通常のSystemVerilog の枠組みでシミュレーションすることができ、移植性も比較的高い方法です。
まずは ROM の初期化ファイルを用意します。48音のうちどの音を鳴らすのか、1行に1拍ずつ48ビットのデータを16進数で書いていきます。今回は W. A. モーツァルトのアイネ・クライネ・ナハトムジーク (Eine Kleine Nachtmusik, K. 515) の1楽章を例として採り上げ、16分音符を1拍としてデータを作成し、eknm.mem というファイル名で保存しました。冒頭の部分は次のような感じです。
001011081000
001011081000
001011081000
001011081000
000000000000
000000000000
000080080080
000080080080
...48ビットですので、1行に12桁の16進数が並びます。完全なファイルは、Gist からダウンロード可能ですが、これが 880 行並んでいます。これでも曲の途中までです。もちろん、こんなもの手動で書いていられません。適宜、記譜ソフト等で作成したデータから変換するスクリプトを作ったりすることになりますが、そのあたりの話は本筋から外れますので割愛します。
ROM テーブルは SystemVerilog では配列として記述するのが自然です。合成属性を記述することで、BRAM を推論して欲しいという希望を Vivado に伝えることができます。また、initial 文で $readmemh にデータファイル名を与え、テーブルを初期化することができます。具体的な記述例を示します。
localparam int N_TACTS = 880; // データの行数
...
// ROM を BRAM として推論させファイルで初期化
(* rom_style = "block" *) logic [47:0] play_mem[N_TACTS];
initial $readmemh("eknm.mem", play_mem);ここでは N_TACTS が初期化データの総行数を示すパラメータです。また、(* rom_style = “block” *) が BRAM 推論の合成属性です。これは SystemVerilog の文法としてはコメントの扱いとなりますので、Vivado 以外の合成ツールやシミュレータで読み込んだ場合でも、エラーとはならずに単に読み飛ばされます。
ROM を読み出す記述は次のとおりです。
// ROM の読み出し
logic [47:0] play_mem_out;
always @(posedge clk) begin
play_mem_out <= play_mem[addr];
endここでは ROM サイズが大きくなった場合のことも考えて出力をレジスタにしていますが、880ワード程度であればレジスタにしなくても問題は生じません。お好みで設計してください。合成時に
[Synth 8-3876] $readmem data file 'eknm.mem' is read successfully ["/.../autoplayer.sv":61]
のようなメッセージが表示されれば、データファイルはうまく読み込まれています。
入力の同期微分と状態遷移
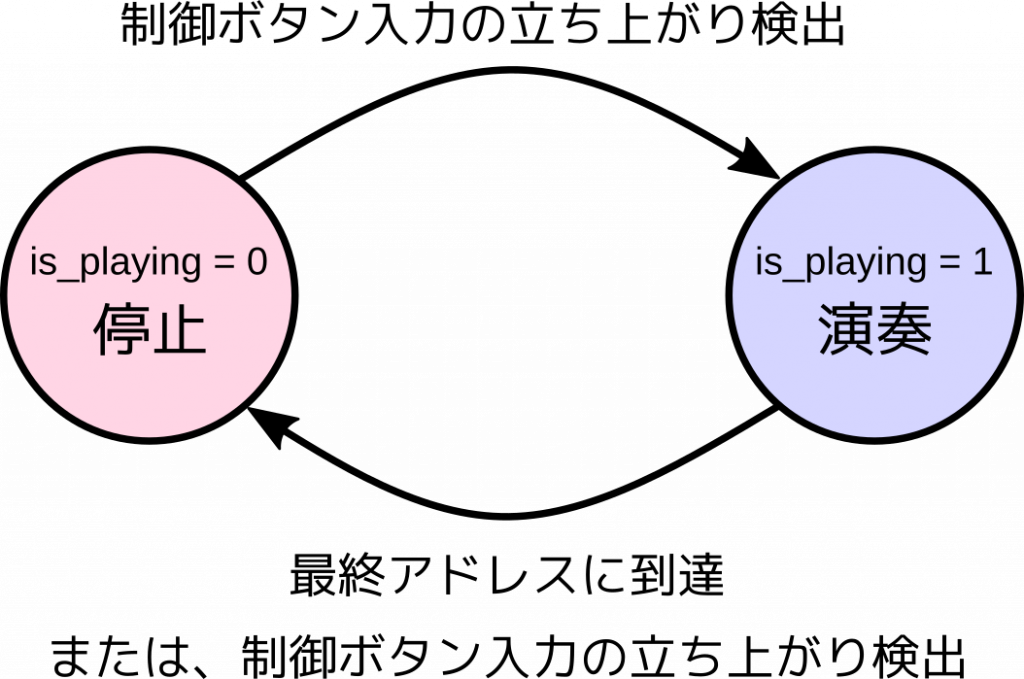
常に自動演奏されるのも煩わしいので、演奏と停止をスイッチボタンでコントロールできるようにします。まだ使っていなかった Arty の RESET ボタンは、ユーザ回路が自由に使うこともできますので、これを使うことにします。もちろん、ROM のアドレスが最後まで行ったらスイッチボタンに関係なく演奏終了です。状態遷移図は次のようになります。
2状態ですので、1ビットの状態レジスタ is_playing を設けています。正弦波生成モジュールも似たような状態遷移図でしたが、制御ボタンの入力が0か1かで状態を遷移するのではなく、制御ボタン信号の立ち上がりを検出する必要がある点が異なります。これはボタンを長く押しつづけたときに、演奏と停止を行ったり来たりするのを避けるためです。
要はボタンが押されたときに1クロックだけ1になる信号が欲しいのですが、そのようなパルスを作る回路が同期微分回路です。名前はややこしいですが、1ビットのレジスタを用意しておき、「1クロック前の値が0で、現在の値が1なら1を出力する」という動作する単純な回路です。記述例を示します。
// 制御ボタン入力の立ち上がりエッジ検出
always @(posedge clk) begin
ctrl_in_prev <= ctrl_in;
end
assign ctrl_pressed = ctrl_in & (!ctrl_in_prev);ctrl_in が RESET ボタンの入力で、ctrl_in_prev が1クロック前の値を保持するためのレジスタです。Arty ではこのボタンはアクティブ Low なのですが、ややこしいのでトップモジュール側で極性を反転させています。もちろん、ボタン入力なのでシンクロナイザとデバウンサが必要になりますが、これもトップモジュール側で処理されていることを前提としています。
is_playing の状態遷移の記述例です。
// 演奏開始・停止の状態制御
always @(posedge clk) begin
if (!is_playing && ctrl_pressed)
is_playing <= 1'b1;
else if (is_playing && addr == (N_TACTS-1) && count == (N_COUNTS-1))
is_playing <= 1'b0;
else if (is_playing && ctrl_pressed)
is_playing <= 1'b0;
endここで N_TACSTS は先ほども出てきましたが、演奏するトータルの拍数です。一方、N_COUNTS は1拍が何クロックなのかを表すパラメータです。
テンポの指定
では、その N_COUNTS をどうやって求めるかです。今回はテンポをメトロノーム風に、1分間に演奏する4分音符の数で指定するようにしました。また、例によってクロックの周波数もパラメータとして与えるようにしています。
parameter real CLK_FREQ = 100e6, // クロック周波数 (Hz)
parameter real MM = 140 // メトロノームテンポこの設定例では4分音符を1分間に140個演奏するということになりますが、ROM テーブルは4分音符をさらに4分割した16分音符を1拍としてデータを並べていますので、1拍の長さは\[
\frac{60}{140}\times \frac{1}{4}\, \text{s}
\]となります。したがって、クロックの周波数を \(f_c\)、テンポの指定値を \(m\) とすると、1拍のクロック数は、\[
\left\lceil f_c \times\frac{60}{m} \times \frac{1}{4} \right\rceil
\]と表せます。これを SystemVerilog で記述すれば、
localparam int N_COUNTS = $ceil(CLK_FREQ * 60.0 / MM / 4.0); // 16分音符を基準となります。自動演奏モジュールの残りの部分はカウンタだけです。完成版のファイルは Gist からダウンロード可能です。
卒業演奏
いよいよすべての準備が整いましたので、最後の実機動作確認を行いましょう。Arty A7-35T 用のトップモジュールやシミュレーションモジュール、IO ピン割り当てファイルなどを含むすべてのソースコードは Gist からダウンロード可能です。
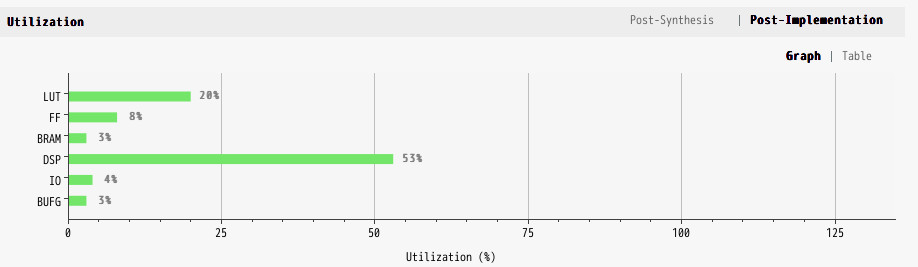
1音につき DSPスライスを1個使いますので、 資源使用率は DSP スライスがもっとも高くなりました (90個のうち48個を使用)。他の資源については2割以下でした。
LUT や FF では、やはりツリー加算器の占める割合が 相当なものです。一方、デルタシグマ変調回路は大変コンパクトで、非同期入力用のデバウンサより小さいです。
それでは動作の様子です。前述のように音はかなり小さめですが、通常のスピーカやイヤフォンであればちゃんと聴こえると思います。複数のボタンを同時に押せば和音が鳴りますし、自動演奏もばっちりですね。
まとめ
- 複数の振動信号を加算すれば和音が出せる
- たくさんのデータの加算を短いレイテンシで足すにはそれなりのハードウェアが必要
- すべての音が同時に鳴ってもオーバーフローしないように気をつける必要がある
- ただし、単音の音量はそのぶん小さくなる
- システムタスク$readmemh を使って ROM テーブルを外部ファイルで初期化できる
さて、本連載では電子ピアノを題材にしながら、電子ピアノ自体のクォリティを上げるとことにはあまり真剣に取り組まず、あれこれ脇道にそれながら進めてきました。今回の題材は完全に遊びですが、それでも要所要所では真面目な開発案件にも使われるテクニックをご紹介しました。楽しみながら、FPGA 利用技術の引き出しを増やせたら最高ですね。
それでは1ビットのパルスが奏でるモーツァルトの名曲とともにお別れです。ごきげんよう、さようなら。
長崎大学・柴田 裕一郎