前回は、最大クリーク問題専用 Dist アルゴリズムの FPGA 実装[1]について述べました。
今回は、実装と性能評価の結果、および、このハードウェアの改良すべき点について述べ、連載を締めくくりたいと思います。
性能評価
実装結果
実装には、台湾の TUL 社製の XIL-ACCEL-RD-KU115 ボードを使用しました 。このボードには、Xilinx 社の Kintex Ultrascale KU115 が搭載されています。4096頂点、400万 エッジのグラフを処理可能なハードウェアを実装したところ、FPGA のリソース消費量は、LUT 17万個 (使用率 26%)、 Block RAM 1555 個 (同・72%) となりました。動作周波数は 110 MHz でした。
性能評価用のベンチマークには、DIMACS benchmark graph [2]を使用しました。これは、最大クリーク問題の性能評価に使用される標準的なベンチマーク問題集で、80題のグラフが収録されています。
今回の実装では、ボード上に搭載されている DRAM を使用しなかったため、DIMACS benchmark graph のうち、特に規模の大きい 2問 (keller6 と C4000.5) を解くことができませんでした。それ以外の問題はすべて処理可能です (ボード上の DRAM を使用すればすべての問題を処理可能となります) 。
処理速度の比較
本節では Dist アルゴリズムのソフトウェア実装および FPGA 実装の処理速度の比較について述べていきます。ソフトウェアの実行環境は Core i7 5820K 3.3 GHz、主記憶 16GB です。
Dist アルゴリズムは局所探索法に基づく発見的解法であり、また、乱数を使用するため、解の精度や処理時間は毎回同じではありません。そのため、どのような尺度で処理時間を測定すればよいのかは結構難しいのですが、今回の評価では以下のようにしました。
- 個々の問題に対して計10回の試行を行う。1回の試行の制限時間は 600 秒とする。
- 既知最適解が得られるまでの時間の平均値を求め、これを処理時間とする。制限時間内に既知最適解に達しなかった試行は除外する (裏返すと、10回のうち 1回でも既知最適解に達していれば、そのときの実行時間をその問題に対する処理時間とする、ということです) 。
- グラフを Partial MaxSAT に変換するための時間を含める。
ここで既知最適解とは、これまでに判明している最も大きいクリークのことです (厳密な意味での最適解とは限りません。問題によっては厳密解がわかっているものもあれば、そうでないものもあります) 。以上をまとめると、既知最適解に達するまでの平均実行時間 (Partial MaxSAT に変換するためにかかる時間を含む) で性能比較を行った、ということです。
なお、ソフトウェアと FPGA のどちらにおいても1秒未満で既知最適解に到達した 43 題は、評価の対象から除外しました。
残る 37 題のうち既知最適解に到達したのは、ソフトウェアでは 28題、FPGA では 27題となりました。同じアルゴリズムを実行しているにもかかわらず、FPGA の方が1題減ってしまい、見つかる解の精度が低下していることを示唆する結果となりました (前回の記事でも触れましたが、フリップされる変数の選択をリダクションツリーで実行することの影響ではないかと考えています) 。
既知最適解に達したケースの評価結果の一部を表1に示します (すべての評価結果に興味のある方は、文献[1]をご覧ください)。
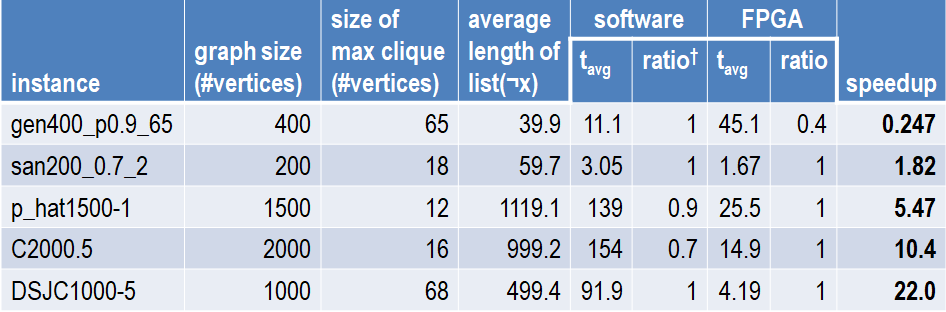
表1において、graph size は頂点の数、size of max clique は既知最適解における頂点の数、average length of list(x) は、各ベンチマークにおける list(x) の長さの平均値を表しています (list(x) の定義は前々回の記事をご覧ください)。tavg は処理時間、ratio は既知最適解に達した試行の割合、speedup は FPGA と ソフトウェアの tavg の比を表しています。
動作周波数 110 MHz にもかかわらず最大22倍程度の高速化ができたということで、まずまずの結果ではないかと思っていますが、ソフトウェアの1/4程の性能しか出なかったケースもありました。
FPGA の方では、変数のフリップに際して実行される hard score のアップデートを並列処理することで性能を出しているのですが、このときの並列度は list(x) の長さに比例します。そのため、 gen400_p0.9_65 のように list(x) が短いケースでは、高速化が難しくなっています。 詳細は省きますが、 list(x) の長さはグラフの疎密によって決まり、密なグラフほど短くなります。そのため、本ハードウェアは疎なグラフのクリークを見つけるケースに有効であると考えられます。
課題
主として、(1) 解の精度、(2) より大規模なグラフの取り扱い、(3) 密なグラフの高速化、(4) 処理可能な応用の拡張の4点です。
(1) 上述のように、解の精度の面でデグレードが起きていることを示唆する結果となりました。その原因をより詳しく調べる必要があります。
(2) に関しては、ボード上の DRAM を使用することで取り扱い可能になると思われます。現在の FPGA には、 Block RAM より大規模なオンチップメモリである Ultra RAM が搭載されているため、それを併用してもよいでしょう。
(3) に関しては、 Dist アルゴリズムでは根本解決が難しく、他のアルゴリズムを用いる必要があると思われます。
(4) 今回は、対象を最大クリーク問題に絞ることで Dist アルゴリズムの簡略化を行いましたが、応用を広げるには、簡略化により省略された箇所の実装が必要となります。
私見では、有力なソフトウェアアルゴリズムとハードウェア化に適したアルゴリズムは一致することの方が珍しいので、 FPGA へ実装することを前提に、ハードウェア開発者自身の手でアルゴリズム開発から始めるべきなのかも知れません。
おわりに
この連載では、FPGA を用いて「組合せ問題」を高速に処理する試みについて述べてきました。
今後、組合せ問題に対する FPGA 研究が盛り上がるか廃れるかはわかりませんが、筆者自身は、この問題を研究する意義と自身の興味の続く限り今後も研究を進めていければと思っています。
お読みいただきありがとうございました。
筑波大学 金澤 健治
参考文献
[1] Kanazawa, K., & Cai, S., “FPGA acceleration to solve maximum clique problems encoded into partial MaxSAT,” IEEE 12th International Symposium on Embedded Multicore/Many-core Systems-on-Chip, pp. 217-224, 2018.
[2] D. S. Johnson and M. A. Trick, “Cliques, coloring, and satisfiability: second DIMACS implementation challenge”, American Mathematical Society, 1996
付録: ソースコード (抜粋)
ソースコードの一部を掲載します (C で記述。ハードウェア関数全体では2000行程度となりました。デッドコードを除くとその半分くらいだと思います。ベタ書きに近い書き方をしている箇所を改めるともっと減るかも知れません) 。
マクロ定義、型宣言、処理の本体
//宣言
#define MV 4096
#define INBUF 1
#define NOTINBUF 0
#define HBUF 0b00000100
#define SSCBUF 0b00000011
#define SBUF 0b00000010
#define SCBUF 0b00000001
#define NOBUF 0b00000000
#define S_WIDTH 32//64
#define C_WIDTH 32//64
#define BANK_S_INDEX 0x001f
#define TAG_S_WIDTH 5
#define NUM_SC MV
#define SC_TABLE_WIDTH 64
#define HC_MAX 4*1024*1024
#define MAX_CLAUSES HC_MAX+128
#define LIT_MASK 0x00003fff
#define V_MASK 0x00001fff
#define NEG_POSITION 0x00002000
#define VAR_INVALID 0x00001001
#define V_WIDTH 13
#define L_WIDTH 14
#define NEG_LOCATION 13
#define NEG_POS 0x8000
#define NEG_POS_IN 0b1000000000000
#define TMPBUF_DEPTH 128*8*16/C_WIDTH
#define CLIST_DEPTH 1024*80 //110 for keller6
#define LT_MASK 0x0000001f
#define BANK_INDEX 0x001f
#define TAG_WIDTH 5
#define HC_NUM_WIDTH 22
typedef int sc_sat_cnt_width;
typedef int soln_width;
typedef char pb_width;
typedef short score_width;
typedef short t_clist;
typedef char exist_width;
typedef short t_clist_in;
// 処理の本体(抜粋)
for (s = 1; s < maxflip; ++s)
{
//reduction tree で選択
flipvar = sel_var_by_existence(existence,rnd_sc,nv_);
//選ばれたものがSOFT節だったら選び直し(バッファから乱択)
if(existence[flipvar] == SCBUF) flipvar = select_var_from_cand_sc_buf(sc._buf, &sc._tail, inscbuf_, k_sscore_, &rnd_sc[(MV/S_WIDTH)/2-1], k_minvtbl);
//選択された変数xfをフリップ、hard scoreの更新
flip_neo_2nd_mc(flipvar, existence,&sc, &num_usc,inscbuf_, k_clist, k_ref, k_clist_cnt, k_hscore_, k_sscore_, k_cur_soln_, &num_uhc);
//実行可能解かどうかの判定
if(num_uhc==0 && (num_usc < opt_num_usc ||k_feasible == 0)){
k_feasible = 1;
opt_num_usc = num_usc;
// 目標精度なら打ち切り
if(opt_num_usc <= goal) break;
}
}リダクションツリーを用いた status の比較に基づく変数の選択
t_clist sel_var_by_existence (
exist_width existence[MV+S_WIDTH], //status table
unsigned int rnd_sc[(MV/S_WIDTH)/2], //乱択用の乱数
t_clist num_vars_ //デバッグ用(有り得ない変数が入ってきたら中止)
)
{
exist_width tmp[S_WIDTH/2];
exist_width tmp1[S_WIDTH/4];
exist_width tmp2[S_WIDTH/8];
exist_width tmp3[S_WIDTH/16];
t_clist tmpidx[S_WIDTH/2];
t_clist tmpidx1[S_WIDTH/4];
t_clist tmpidx2[S_WIDTH/8];
t_clist tmpidx3[S_WIDTH/16];
exist_width tmpsel[MV/S_WIDTH];
exist_width tmpsel1[(MV/S_WIDTH)/2];
exist_width tmpsel2[(MV/S_WIDTH)/4];
exist_width tmpsel3[(MV/S_WIDTH)/8];
exist_width tmpsel4[(MV/S_WIDTH)/16];
exist_width tmpsel5[(MV/S_WIDTH)/32];
exist_width tmpsel6[(MV/S_WIDTH)/64];
t_clist tmpidxsel[MV/S_WIDTH];
t_clist tmpidxsel1[(MV/S_WIDTH)/2];
t_clist tmpidxsel2[(MV/S_WIDTH)/4];
t_clist tmpidxsel3[(MV/S_WIDTH)/8];
t_clist tmpidxsel4[(MV/S_WIDTH)/16];
t_clist tmpidxsel5[(MV/S_WIDTH)/32];
t_clist tmpidxsel6[(MV/S_WIDTH)/64];
#pragma HLS array_partition variable=tmpidx complete
#pragma HLS array_partition variable=tmpidx1 complete
#pragma HLS array_partition variable=tmpidx2 complete
#pragma HLS array_partition variable=tmpidx3 complete
#pragma HLS array_partition variable=tmpidxsel complete
#pragma HLS array_partition variable=tmpidxsel1 complete
#pragma HLS array_partition variable=tmpidxsel2 complete
#pragma HLS array_partition variable=tmpidxsel3 complete
#pragma HLS array_partition variable=tmpidxsel4 complete
#pragma HLS array_partition variable=tmpidxsel5 complete
#pragma HLS array_partition variable=tmpidxsel6 complete
#pragma HLS array_partition variable=tmp complete
#pragma HLS array_partition variable=tmp1 complete
#pragma HLS array_partition variable=tmp2 complete
#pragma HLS array_partition variable=tmp3 complete
#pragma HLS array_partition variable=tmpsel complete
#pragma HLS array_partition variable=tmpsel1 complete
#pragma HLS array_partition variable=tmpsel2 complete
#pragma HLS array_partition variable=tmpsel3 complete
#pragma HLS array_partition variable=tmpsel4 complete
#pragma HLS array_partition variable=tmpsel5 complete
#pragma HLS array_partition variable=tmpsel6 complete
int st_add[S_WIDTH];
#pragma HLS array_partition variable=st_add complete
t_clist idxselected;
for (int j = 0;j < MV/S_WIDTH;j++){
#pragma HLS unroll
tmpidxsel[j] = VAR_INVALID;
tmpsel[j] = NOBUF;
}
//1st reduction tree
for(int j = 0;j < MV/S_WIDTH;j++){
#pragma HLS pipeline
for (int i = 0;i < S_WIDTH;i++) {
if(existence[i+j*S_WIDTH] == HBUF)st_add[i] = 3;
else if (existence[i+j*S_WIDTH] == SBUF || existence[i+j*S_WIDTH] == SSCBUF)st_add[i] = 2;
else if (existence[i+j*S_WIDTH] == SCBUF)st_add[i] = 1;
else st_add[i] = 0;
}
for(int i = 0;i < (MV/S_WIDTH)/2;i++) m_rnd(&rnd_sc[i]); //M系列乱数
for (int i = 0;i < S_WIDTH/2;i++) {
if(st_add[2*i] > st_add[2*i+1]){
tmp[i] = st_add[2*i];
tmpidx[i] = 2*i+j*S_WIDTH;
}
else if (st_add[2*i] < st_add[2*i+1]) {
tmp[i] = st_add[2*i+1];
tmpidx[i] = 2*i+1+j*S_WIDTH;
}
else {
tmp[i] = st_add[2*i+(rnd_sc[0]&0x00000001)];//[2*i+k][j];
tmpidx[i] = 2*i+j*S_WIDTH+(rnd_sc[0]&0x00000001);
}
}
for (int i = 0;i < S_WIDTH/4;i++) {
if(tmp[2*i] > tmp[2*i+1]){
tmp1[i] = tmp[2*i];
tmpidx1[i] = tmpidx[2*i];
}
else if (tmp[2*i] < tmp[2*i+1]) {
tmp1[i] = tmp[2*i+1];
tmpidx1[i] = tmpidx[2*i+1];
}
else {
tmp1[i] = tmp[2*i+(rnd_sc[1]&0x00000001)];
tmpidx1[i] = tmpidx[2*i+(rnd_sc[1]&0x00000001)];
}
}
for (int i = 0;i < S_WIDTH/8;i++) {
if(tmp1[2*i] > tmp1[2*i+1]){
tmp2[i] = tmp1[2*i];
tmpidx2[i] = tmpidx1[2*i];
}
else if (tmp1[2*i] < tmp1[2*i+1]) {
tmp2[i] = tmp1[2*i+1];
tmpidx2[i] = tmpidx1[2*i+1];
}
else {
tmp2[i] = tmp1[2*i+(rnd_sc[2]&0x00000001)];
tmpidx2[i] = tmpidx1[2*i+(rnd_sc[2]&0x00000001)];
}
}
for (int i = 0;i < S_WIDTH/16;i++) {
if(tmp2[2*i] > tmp2[2*i+1]){
tmp3[i] = tmp2[2*i];
tmpidx3[i] = tmpidx2[2*i];
}
else if (tmp2[2*i] < tmp2[2*i+1]) {
tmp3[i] = tmp2[2*i+1];
tmpidx3[i] = tmpidx2[2*i+1];
}
else {
tmp3[i] = tmp2[2*i+(rnd_sc[3]&0x00000001)];
tmpidx3[i] = tmpidx2[2*i+(rnd_sc[3]&0x00000001)];
}
}
if(tmp3[0] > tmp3[1]){
tmpsel[j] = tmp3[0];
tmpidxsel[j] = tmpidx3[0];
}
else if (tmp3[0] < tmp3[1]) {
tmpsel[j] = tmp3[1];
tmpidxsel[j] = tmpidx3[1];
}
else {
tmpidxsel[j] = tmpidx3[rnd_sc[8] & 0x00000001];
tmpsel[j] = tmp3[rnd_sc[8] & 0x00000001];
}
if(j*S_WIDTH+1 > num_vars_) break;
}
//2nd reduction tree
for(int i = 0;i < (MV/S_WIDTH)/2;i++){
#pragma HLS unroll
m_rnd(&rnd_sc[i]);
}
for (int i = 0;i < (MV/S_WIDTH)/2;i++) {
#pragma HLS unroll
if(tmpsel[2*i] > tmpsel[2*i+1]){
tmpsel1[i] = tmpsel[2*i];
tmpidxsel1[i] = tmpidxsel[2*i];
}
else if (tmpsel[2*i] < tmpsel[2*i+1]) {
tmpsel1[i] = tmpsel[2*i+1];
tmpidxsel1[i] = tmpidxsel[2*i+1];
}
else {
tmpsel1[i] = tmpsel[2*i+(rnd_sc[i]&0x00000001)];
tmpidxsel1[i] = tmpidxsel[2*i+(rnd_sc[i]&0x00000001)];
}
}
for(int i = 0;i < (MV/S_WIDTH)/2;i++){
#pragma HLS unroll
m_rnd(&rnd_sc[i]);
}
for (int i = 0;i < MV/S_WIDTH/4;i++) {
#pragma HLS unroll
if(tmpsel1[2*i] > tmpsel1[2*i+1]){
tmpsel2[i] = tmpsel1[2*i];
tmpidxsel2[i] = tmpidxsel1[2*i];
}
else if (tmpsel1[2*i] < tmpsel1[2*i+1]) {
tmpsel2[i] = tmpsel1[2*i+1];
tmpidxsel2[i] = tmpidxsel1[2*i+1];
}
else {
tmpsel2[i] = tmpsel1[2*i+(rnd_sc[i]&0x00000001)];
tmpidxsel2[i] = tmpidxsel1[2*i+(rnd_sc[i]&0x00000001)];
}
}
for(int i = 0;i < (MV/S_WIDTH)/2;i++){
#pragma HLS unroll
m_rnd(&rnd_sc[i]);
}
for (int i = 0;i < MV/S_WIDTH/8;i++) {
#pragma HLS unroll
if(tmpsel2[2*i] > tmpsel2[2*i+1]){
tmpsel3[i] = tmpsel2[2*i];
tmpidxsel3[i] = tmpidxsel2[2*i];
}
else if (tmpsel2[2*i] < tmpsel2[2*i+1]) {
tmpsel3[i] = tmpsel2[2*i+1];
tmpidxsel3[i] = tmpidxsel2[2*i+1];
}
else {
tmpsel3[i] = tmpsel2[2*i+(rnd_sc[i]&0x00000001)];
tmpidxsel3[i] = tmpidxsel2[2*i+(rnd_sc[i]&0x00000001)];
}
}
for(int i = 0;i < (MV/S_WIDTH)/2;i++){
#pragma HLS unroll
m_rnd(&rnd_sc[i]);
}
for (int i = 0;i < MV/S_WIDTH/16;i++) {
#pragma HLS unroll
if(tmpsel3[2*i] > tmpsel3[2*i+1]){
tmpsel4[i] = tmpsel3[2*i];
tmpidxsel4[i] = tmpidxsel3[2*i];
}
else if (tmpsel3[2*i] < tmpsel3[2*i+1]) {
tmpsel4[i] = tmpsel3[2*i+1];
tmpidxsel4[i] = tmpidxsel3[2*i+1];
}
else {
tmpsel4[i] = tmpsel3[2*i+(rnd_sc[i]&0x00000001)];
tmpidxsel4[i] = tmpidxsel3[2*i+(rnd_sc[i]&0x00000001)];
}
}
for(int i = 0;i < (MV/S_WIDTH)/2;i++){
#pragma HLS unroll
m_rnd(&rnd_sc[i]);
}
for (int i = 0;i < MV/S_WIDTH/32;i++) {
#pragma HLS unroll
if(tmpsel4[2*i] > tmpsel4[2*i+1]){
tmpsel5[i] = tmpsel4[2*i];
tmpidxsel5[i] = tmpidxsel4[2*i];
}
else if (tmpsel4[2*i] < tmpsel4[2*i+1]) {
tmpsel5[i] = tmpsel4[2*i+1];
tmpidxsel5[i] = tmpidxsel4[2*i+1];
}
else {
tmpsel5[i] = tmpsel4[2*i+(rnd_sc[i]&0x00000001)];
tmpidxsel5[i] = tmpidxsel4[2*i+(rnd_sc[i]&0x00000001)];
}
}
for(int i = 0;i < MV/S_WIDTH/2;i++){
#pragma HLS unroll
m_rnd(&rnd_sc[i]);
}
for (int i = 0;i < MV/S_WIDTH/64;i++) {
#pragma HLS unroll
if(tmpsel5[2*i] > tmpsel5[2*i+1]){
tmpsel6[i] = tmpsel5[2*i];
tmpidxsel6[i] = tmpidxsel5[2*i];
}
else if (tmpsel5[2*i] < tmpsel5[2*i+1]) {
tmpsel6[i] = tmpsel5[2*i+1];
tmpidxsel6[i] = tmpidxsel5[2*i+1];
}
else {
tmpsel6[i] = tmpsel5[2*i+(rnd_sc[i]&0x00000001)];
tmpidxsel6[i] = tmpidxsel5[2*i+(rnd_sc[i]&0x00000001)];
}
}
if(tmpsel6[0] > tmpsel6[1]){
idxselected = tmpidxsel6[0];
}
else if (tmpsel6[0] < tmpsel6[1]) {
idxselected = tmpidxsel6[1];
}
else {
idxselected = tmpidxsel6[rnd_sc[(MV/S_WIDTH)/2-1] & 0x00000001];
}
return idxselected;
}変数のフリップと hard score/soft score,status の更新
void flip_neo_2nd_mc(
t_clist flipvar, //xf
exist_width existence_[MV+S_WIDTH], //status table
cbuf *sc,//unsatsified soft clause buffer
int *num_usc, //unsatisfied soft clause bufferの要素数
pb_width _inscbuf_[C_WIDTH][MV/C_WIDTH+1], //既にbuffer内に格納済みか?(重複格納防止用)
t_clist_in clist[CLIST_DEPTH][C_WIDTH], // clause list table
int clist_cnt[MV+1][2],
int ref[MV+1][2], // reference table
score_width k_hscore_[C_WIDTH][MV/C_WIDTH+1], //hard score table
score_width k_sscore_[C_WIDTH][MV/C_WIDTH+1], //soft score table
soln_width k_cur_soln_[C_WIDTH][MV/C_WIDTH+1], //variable truth table
int *num_uhc //非充足な hard節の数
)//MAX-2SAT only
{
#pragma HLS DEPENDENCE variable=existence_ inter RAW false
#pragma HLS DEPENDENCE variable=k_hscore_ inter RAW false
#pragma HLS DEPENDENCE variable=k_sscore_ inter RAW false
#pragma HLS DEPENDENCE variable=_inscbuf_ inter RAW false
#pragma HLS DEPENDENCE variable=k_cur_soln_ inter RAW false
int clist_head;
int cnt;
int sig; //0:positive, 1: negative(senseと逆)
t_clist var[C_WIDTH]; //list(xf)内の変数
soln_width val_f; //xf(flipされる変数)の真理値
soln_width val[C_WIDTH];//list(xf)内の変数の真理値
bool neg[C_WIDTH]; //否定の有無
int diff_uhc[C_WIDTH]; //list(xf)内の変数のhard score増分
score_width mid_hscore[C_WIDTH],mid_sscore[C_WIDTH];
t_clist valid[C_WIDTH];
bool eval[C_WIDTH];
score_width org_flipvar_hscore; //flip前のxfのhard score
score_width org_flipvar_sscore; //flip前のxfのsoft score
int f_raddr = flipvar & BANK_INDEX;
int f_caddr = flipvar >> TAG_WIDTH;
int raddr[C_WIDTH],caddr[C_WIDTH];
static int diff_cnt;
int tmpdiffuhc[C_WIDTH/2];
int tmpdiffuhc1[C_WIDTH/4];
int tmpdiffuhc2[C_WIDTH/8];
int tmpdiffuhc3[C_WIDTH/16];
#pragma HLS array_partition variable=mid_hscore complete
#pragma HLS array_partition variable=mid_sscore complete
#pragma HLS array_partition variable=var complete
#pragma HLS array_partition variable=val complete
#pragma HLS array_partition variable=neg complete
#pragma HLS array_partition variable=diff_uhc complete
//#pragma HLS array_partition variable=en complete
#pragma HLS array_partition variable=valid complete
#pragma HLS array_partition variable=raddr complete
#pragma HLS array_partition variable=caddr complete
#pragma HLS array_partition variable=eval complete
#pragma HLS array_partition variable=tmpdiffuhc complete
#pragma HLS array_partition variable=tmpdiffuhc1 complete
#pragma HLS array_partition variable=tmpdiffuhc2 complete
#pragma HLS array_partition variable=tmpdiffuhc3 complete
//#pragma HLS DEPENDENCE variable=tmpdiffuhc3 inter RAW false
//旧
//k_cur_soln_[f_raddr][f_caddr] = 1 - k_cur_soln_[f_raddr][f_caddr];
//val_f = k_cur_soln_[f_raddr][f_caddr];//k_cur_soln[flipvar];
//新
//xfのフリップ、hscore(xf)、sscore(xf)の更新
val_f = 1-k_cur_soln_[f_raddr][f_caddr];//k_cur_soln[flipvar];
org_flipvar_hscore = k_hscore_[f_raddr][f_caddr];
org_flipvar_sscore = k_sscore_[f_raddr][f_caddr];
k_cur_soln_[f_raddr][f_caddr] = 1 - k_cur_soln_[f_raddr][f_caddr];
k_hscore_[f_raddr][f_caddr] = -org_flipvar_hscore;
k_sscore_[f_raddr][f_caddr] = -org_flipvar_sscore;
//偽ならxfをunsatisfied soft clause bufferに追加、真なら削除
if (k_cur_soln_[f_raddr][f_caddr] == 0) {
(*num_usc)++;
if(_inscbuf_[f_raddr][f_caddr] != INBUF){
_inscbuf_[f_raddr][f_caddr] = INBUF;
sc->_buf[(sc->_tail)++] = flipvar;
}
existence_[flipvar] = SCBUF;
}
else {
(*num_usc)--;
existence_[flipvar] = NOBUF;
}
//xfのstatus 更新
if (k_hscore_[f_raddr][f_caddr] > 0) {
existence_[flipvar] = HBUF;
}
else if (k_hscore_[f_raddr][f_caddr] == 0 && k_sscore_[f_raddr][f_caddr] > 0) {
existence_[flipvar] = SSCBUF;
}
for(int z = 0;z < C_WIDTH;z++){
#pragma HLS unroll
diff_uhc[z] = 0;
}
//list tableを読み、hard score の更新
for (sig = 0;sig < 2;sig++) {
if ((clist_head = ref[flipvar][sig]) == 0) continue;
//==0のときはそのリテラルを含むクローズは存在しない
cnt = clist_cnt[flipvar][sig]; //list tableを読み出す回数
for (int z = 0; z < MV/(C_WIDTH/2);z++,clist_head++) {
#pragma HLS pipeline
//32変数ずつ読出
for(int i = 0;i < C_WIDTH;i++) valid[i] = clist[clist_head][i] & LIT_MASK;
for (int i = 0;i < C_WIDTH;i++) {
var[i] = valid[i] & V_MASK;
neg[i] = valid[i] >> V_WIDTH;
}
//hard score/soft scoreの読出
for (int i = 0;i < C_WIDTH;i++) caddr[i] = var[i] >> TAG_WIDTH;
for (int i = 0;i < C_WIDTH;i++) {
mid_hscore[i] = k_hscore_[i][caddr[i]];
mid_sscore[i] = k_sscore_[i][caddr[i]];
val[i] = k_cur_soln_[i][caddr[i]];
}
//hard節の真理値計算
for (int i = 0;i < C_WIDTH;i++) eval[i] = (val_f ^ sig) ^ (val[i] ^ neg[i]);
//hard score更新 (差分を計算)
for (int i = 0;i < C_WIDTH;i++) {
if(eval[i] == 0 && (var[i] != VAR_INVALID)){
mid_hscore[i] ++;
if((val_f ^ sig) == 0) diff_uhc[i] ++;
}
else if(eval[i] == 1 && (var[i] != VAR_INVALID)){
mid_hscore[i] --;
if((val_f ^ sig) == 1) diff_uhc[i] --;
}
}
for (int i = 0;i < C_WIDTH;i++) k_hscore_[i][caddr[i]] = mid_hscore[i];
// status更新
for (int i = 0;i < C_WIDTH;i++) {
if (mid_hscore[i] > 0 ) existence_[i+C_WIDTH*caddr[i]] = HBUF;
else if (mid_hscore[i] == 0 && mid_sscore[i] > 0) existence_[i+C_WIDTH*caddr[i]] = SSCBUF;
else if (mid_sscore[i] > 0)existence_[i+C_WIDTH*caddr[i]] = SCBUF;
else existence_[i+C_WIDTH*caddr[i]] = NOBUF;
}//c
//次の32個を読出
cnt--;
//全部処理したら終了
if (cnt <= 0)break;
}//z
}
// 非充足なhard節の数を更新(adderのtree)
for (int z = 0;z < C_WIDTH/2;z++) {
#pragma HLS unroll
tmpdiffuhc[z] = diff_uhc[2*z]+diff_uhc[2*z+1];
}
for (int z = 0;z < C_WIDTH/4;z++) {
#pragma HLS unroll
tmpdiffuhc1[z] = tmpdiffuhc[2*z]+tmpdiffuhc[2*z+1];
}
for (int z = 0;z < C_WIDTH/8;z++) {
#pragma HLS unroll
tmpdiffuhc2[z] = tmpdiffuhc1[2*z]+tmpdiffuhc1[2*z+1];
}
for (int z = 0;z < C_WIDTH/16;z++) {
#pragma HLS unroll
tmpdiffuhc3[z] = tmpdiffuhc2[2*z]+tmpdiffuhc2[2*z+1];
}
(*num_uhc) += tmpdiffuhc3[0]+tmpdiffuhc3[1];
}