FPGA を使って基本的なアルゴリズムのソーティングを劇的に高速化 (5)

前回の記事までは、私たちが国際会議 FCCM 2017 (論文 [1]) で提案した高性能 FPGA ベースのハードウェアマージソータ (Hardware Merge Sorter, HMS) を説明してきました。

コースの最終回となる今回は、その後の研究論文を紹介していきます。

MMS: フィードバックデータパスのない HMS

FCCM 2017 の論文で提案した HMS とそのベースラインは「フィードバックデータパス」を含みます。下図はこれらの基本的な構成要素であるマージロジック回路 (2つのソートされた系列を1つの系列にマージするマージロジック回路) のフィードバックデータパスをハイライトしています。

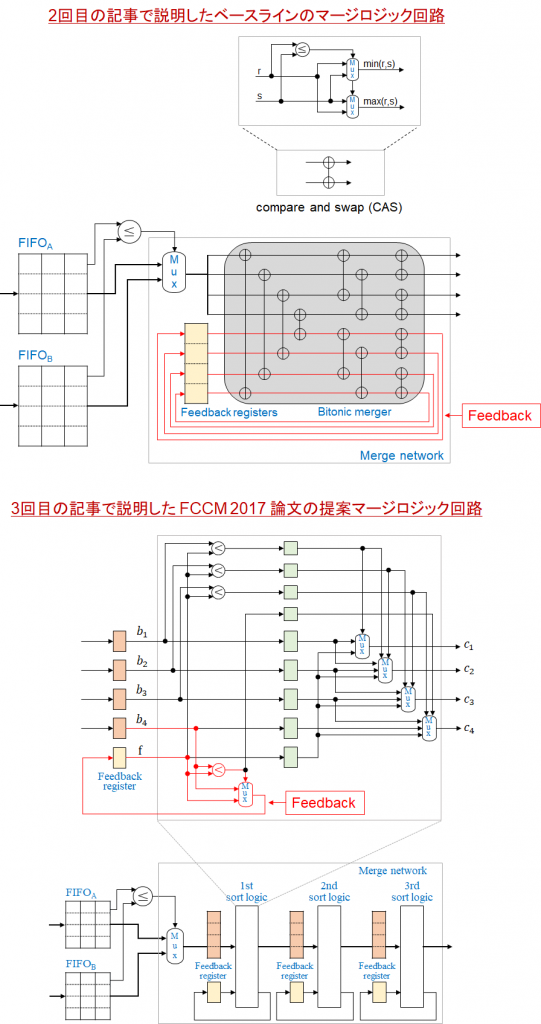
ベースラインのマージロジック回路では、フィードバックデータパスが存在するため、マージャを1サイクルで処理しないといけません。このため、パイプライン処理などで単純にクリティカルパスのゲート段数を削減することは困難です。

FCCM 2017 の論文で提案したマージロジック回路では、マージオペレーションを大きなマージャの代わりに複数の小さなソートロジックで処理することで、クリティカルパスを1個のコンパレータと1個の2入力マルチプレクサに削減できました。しかし、このフィードバックデータパスは、更なる削減を困難にします。

そこで、私たちは、国際会議 FCCM 2018 (論文 [2]) でフィードバックデータパスのないマージロジック回路を提案しました。図2は提案マージロジック回路のカギとなるアイデアとその動作例を示しています。

この例では、2回目と3回目の記事の例のように、1, 3, 5, 7, 9, … というソートされた奇数の系列と、2, 4, 6, 8, 10, … というソートされた偶数の系列をマージして、1つのソートされた系列 1, 2, 3, 4, 5, 6, … を作ります。

FIFO_A と FIFO_B から読み出されたレコードはそれぞれ R_A と R_B というレジスタセットに格納されます。バイトニック・マージャ (bitonic merger) BM_L は R_A と R_B に格納されているレコードをソートして、大きい4個のレコードをバイトニック・マージャ BM_S に出力します。BM_S はこれらのレコードと FIFO_A, FIFO_B からのレコードをソートして、小さい4個のレコードを出力します。

証明の詳細は省略しますが (論文 [2] をご参照ください)、提案するマージロジック回路のカギとなるアイデアは、BM_L が出力する大きい4個のレコードはベースラインのマージロジック回路のフィードバックレジスタに格納される4個のレコードと同じになることです。そのため、提案マージロジック回路は、ベースラインのマージロジック回路のように、2つのソートされた系列を正しくマージできます。

R_A, R_B は、ベースラインのマージロジック回路のフィードバックレジスタのように最小のレコード (この例では0) で初期化します。

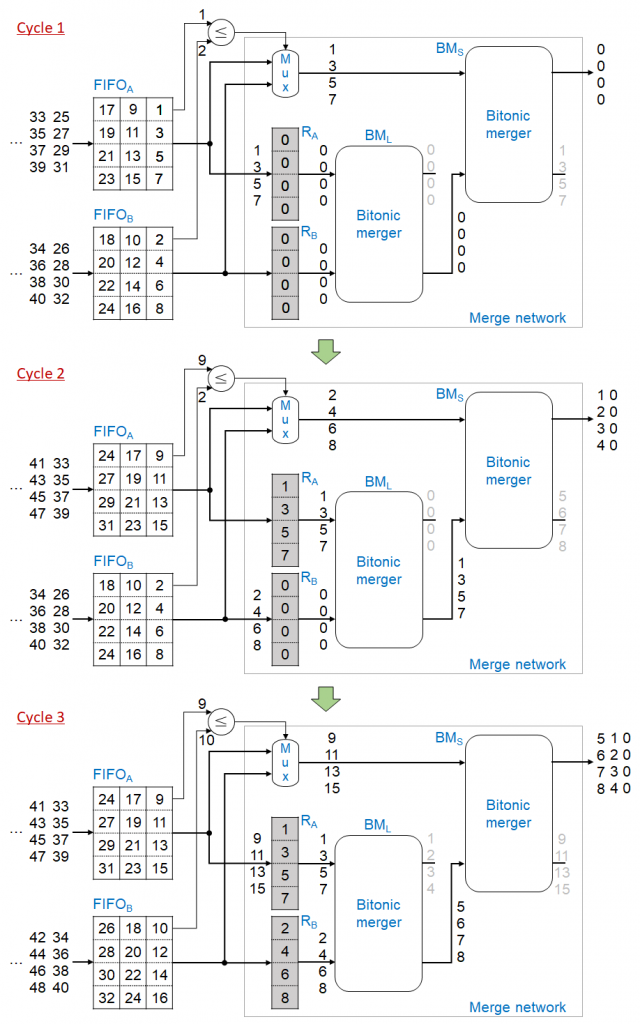
図2の具体的な動作例を説明します。

サイクル1では、FIFO_A の最小レコード1が FIFO_B の最小レコード2より小さいため、FIFO_A から4個のレコード (1, 3, 5, 7) が読み出され、R_A と BM_S に送られます。BM_L は RA と R_B に格納されているレコード (0, 0, 0, 0), (0, 0, 0, 0) をソートして、大きい4個のレコード (0, 0, 0, 0) を BM_S に出力します。BM_S はこれらのレコードと FIFO_A からの4個のレコード (1, 3, 5, 7) をソートして、小さい4個のレコード (0, 0, 0, 0) を出力します。ただし、このサイクルの出力レコード (0, 0, 0, 0) は2つの入力系列のレコードではなく初期状態に R_A, R_B に入るものなので出力系列から除外されます。

サイクル2では、FIFO_B の最小レコード2が FIFO_A の最小レコード9より小さいため、FIFO_B から4個のレコード (2, 4, 6, 8) が読み出され、R_B と BM_S に送られます。BM_L は R_A と R_B に格納されているレコード (1, 3, 5, 7), (0, 0, 0, 0) をソートして、大きい4個のレコード (1, 3, 5, 7) を BM_S に出力します。BM_S はこれらのレコードと FIFO_B からの4個のレコード (2, 4, 6, 8) をソートして、小さい4個のレコード (1, 2, 3, 4) を出力します。

サイクル3では、FIFO_A の最小レコード9が FIFO_B の最小レコード10より小さいため、FIFO_A から4個のレコード (9, 11, 13, 15) が読み出され、R_A と BM_S に送られます。BM_L は R_A と R_B に格納されているレコード (1, 3, 5, 7), (2, 4, 6, 8) をソートして、大きい4個のレコード (5, 6, 7, 8) を BM_S に出力します。BM_S はこれらのレコードと FIFO_B からの4個のレコード (9, 11, 13, 15) をソートして、小さい4個のレコード (5, 6, 7, 8) を出力します。

このように、2つの入力系列が正しくマージされます。

図2のマージロジック回路はフィードバックデータパスを持たないため、処理をパイプライン化してクリティカルパスのゲート段数を削除することが簡単になります。具体的には、BM_L と BM_S 内の compare and swap ユニットを下図のように、2段でパイプライン化すれば回路全体のクリティカルパスは1個のコンパレータのみとなります。

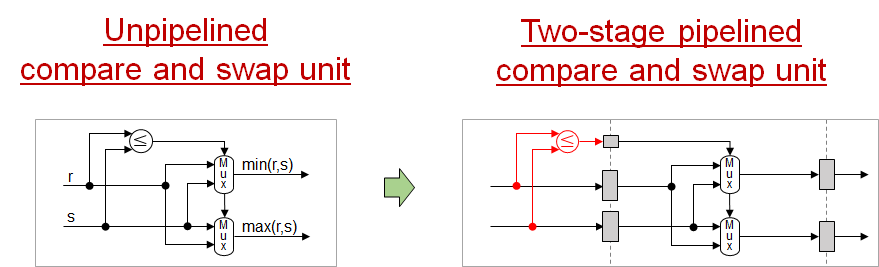
これは、1サイクルあたりの出力レコード数を増やしても一定で変わりません。

クリティカルパスを簡素化することで、FCCM 2018 で提案した HMS (MMS, 上記のフィードバックデータパスのない HMS) は非常に高いソーティング性能を達成しています。

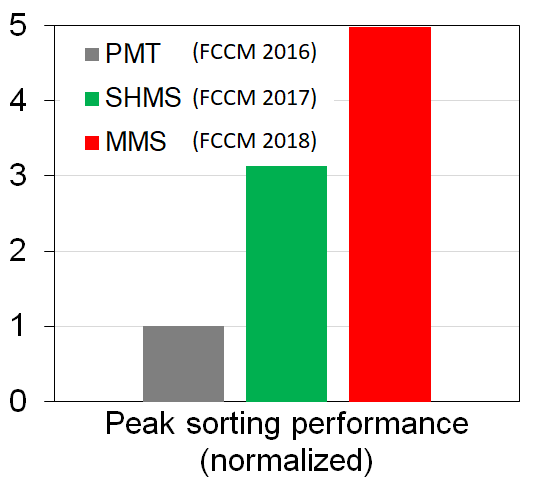
上図に示すように、MMS は FCCM 2017 で提案した SHMS と前回の記事で説明した比較対象の HMS (PMT、論文 [3]) と比較して、約1.6倍と5倍の速度向上を達成しています。

ここで詳細な説明を省略しますが、MMS の1つの問題は、複数のレコードが同じキーを持つとき、キーのみでレコードを比較すれば回路が正しく動作しない場合があることです。MMS はレコード全体比較のアプローチを採用してこの問題を解決しましたが、より効率的なアプローチが存在しています。これは、マージロジック回路の実装でバイトニック・マージャではなくバッチャー奇偶・マージャ (Batcher’s odd–even merger) を使用するアプローチです。具体的な説明、解析、評価は論文 [4] に記載されています。

FLiMS: Fast Lightweight Merge Sorter

次に、国際会議 FPT 2018 （論文 [5]）で発表された FLiMS という HMS を紹介します。FLiMS は SHMS, MMS と別のアルゴリズムを採用します。下図は FLiMS の E レコードのマージロジック回路 (E = 4) とその動作例を示しています。

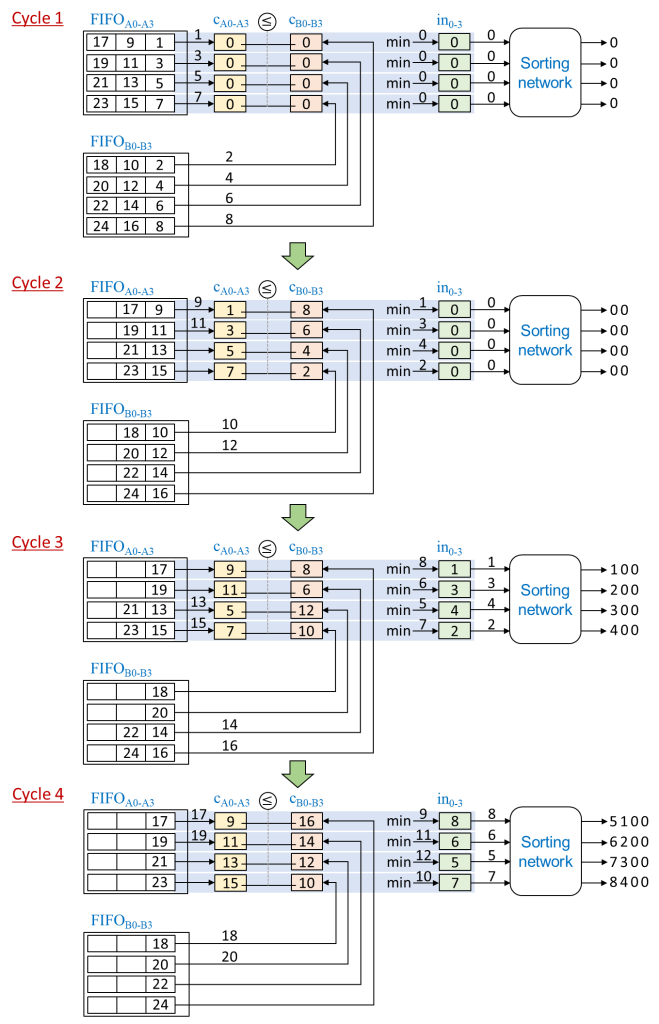
この例では、図2の例のように、ソートされた奇数と偶数の系列をマージします。奇数の系列を a₀, a₁, a₂, … (a₀ = 1, a₁ = 3, a₂ = 5, …) とすると、a₀, a_E, a_2E, … は FIFO_A0、 a₁, a_E+1, a_2E+1, … は FIFO_A1 のようにレコードの格納が E 個の FIFO バッファに分割されます。偶数の系列の格納も同様です。レジスタ c_Ai, c_Bi, in_i (i = 0, 1, …, E-1) は最小のレコード (この例では0) で初期化します。c_Ai は FIFO_Ai、c_Bi は FIFO_Bj (j = E-1-i) に接続されます。

サイクル1では、c_Ai と c_Bi は FIFO_Ai と FIFO_Bj (j = E-1-i) の最小 (先頭) のレコードで更新されます。

サイクル2では、c_Ai と c_Bi が比較されて、小さい方が in_i に格納されます。c_Ai の方が小さければ FIFO_Ai から先頭のレコードを読み出して c_Ai を更新します。逆に、c_Bi の方が小さければ FIFO_Bj (j = E-1-i) から先頭のレコードを読み出して c_Bi を更新します。例えば、c_A0 (1) は c_B0 (8) より小さいため、in₀ に c_A0 のレコード (1) を格納します。同時に、FIFO_A0 から9が読み出されます。このように、 in₁, in₂, in₃ に c_A1, c_B2, c_B3 のレコード (3, 4, 2) を格納、FIFO_A1, FIFO_B1, FIFO_B0 から先頭のレコード (11, 12, 10) を読み出して c_A1, c_B2, c_B3 を更新します。

サイクル3では、ソーティングネットワーク (sorting network) が in₀, in₁, in₂, in₃ に格納されているレコード (1, 3, 4, 2) をソートして、(1, 2, 3, 4) を出力します。サイクル1と2では出力レコード（どちらの場合でも (0, 0, 0, 0)）もありますが、これらは2つの入力系列のレコードではないので出力系列から除外されます。サイクル2の挙動のように、in₀, in₁, in₂, in₃ に c_B0, c_B1, c_A2, c_A3 のレコード (8, 6, 5, 7) を格納します。c_B0, c_B1, c_A2, c_A3 は FIFO_B3, FIFO_B2, FIFO_A2, FIFO_A3 の先頭のレコード (16, 14, 13, 15) で更新されます。

同様に、サイクル4では、ソーティングネットワークは4個のレコード (5, 6, 7, 8) を出力します。in₀, in₁, in₂, in₃ に c_A0, c_A1, c_B2, c_B3 のレコード (9, 11, 12, 10) を格納します。c_A0, c_A1, c_B2, c_B3 は FIFO_A0, FIFO_A1, FIFO_B1, FIFO_B0 の先頭のレコード (17, 19, 20, 18) で更新されます。

このように、2つの入力系列が正しくマージされます。

FLiMS は MMS のように、フィードバックデータパスを持ちません。ソーティングネットワーク内の compare and swap ユニットを図3のように、2段でパイプライン化すれば回路全体のクリティカルパスは1個のコンパレータのみとなります。

まとめと今後の展望

今回は、このコースで紹介した高性能 FPGA ソーティングアクセラレータの代表的な発展研究を説明しました。ソーティングは基本的で重要なアルゴリズムなので、今後、これらのアクセラレータの応用が期待されます。

残された課題の1つは、ソーティングの対象となる様々なデータの種類への対応です。このコースで紹介したどのソーティングアクセラレータも整数のソートを対象としました。しかし、実際にソーティングの対象となるデータは可変長の文字列等で簡単に対応できない場合があり、更なる研究が必要です。

東工大 Thiem Van Chu

参考文献

1. Susumu Mashimo, Thiem Van Chu, and Kenji Kise, “High-Performance Hardware Merge Sorter,” The 25th IEEE International Symposium on Field-Programmable Custom Computing Machines (FCCM), May 2017.
2. Makoto Saitoh, Elsayed A. Elsayed, Thiem Van Chu, Susumu Mashimo, and Kenji Kise, “A High-Performance and Cost-Effective Hardware Merge Sorter without Feedback Datapath,” The 26th IEEE International Symposium on Field-Programmable Custom Computing Machines (FCCM), May 2018.
3. Wei Song, Dirk Koch, Mikel Lujan, and Jim Garside, “Parallel Hardware Merge Sorter,” The 24th IEEE International Symposium on Field-Programmable Custom Computing Machines (FCCM), May 2016.
4. Makoto Saitoh and Kenji Kise, “Very Massive Hardware Merge Sorter,” The 2018 International Conference on Field-Programmable Technology (FPT), December 2018.
5. Philippos Papaphilippou, Chris Brooks, and Wayne Luk, “FLiMS: Fast Lightweight Merge Sorter,” The 2018 International Conference on Field-Programmable Technology (FPT), December 2018.