FPGA で始めるエッジディープラーニング (4)

みなさんこんにちは。この記事は、ACRiブログのDeep Learningコースの第4回目です。

前回の記事では、畳み込み層の C 実装、結果確認を行いました。今回の記事では、残りの未実装レイヤーである全結合層、プーリング層、活性化関数 ReLU の実装をしていきます。

各層の実装

全結合層

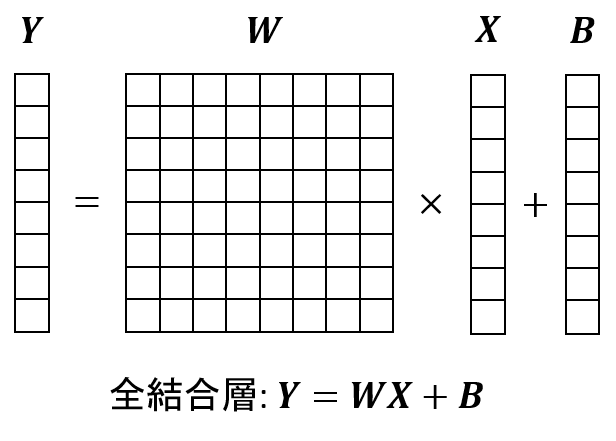
全結合層は入力ベクトル X に対して重み行列 W をかけ、その後バイアス B を加算する処理です。第2回の記事の図を以下に再掲しますが、この図の通りに計算が行えれば良いです。

全結合層の実装は以下になります。

void linear(const float *x, const float* weight, const float* bias,
            int64_t in_features, int64_t out_features, float *y) {
  for (int64_t i = 0; i < out_features; ++i) {
    float sum = 0.f;
    for (int64_t j = 0; j < in_features; ++j) {
      sum += x[j] * weight[i * in_features + j];
    }
    y[i] = sum + bias[i];
  }
}

この関数のインターフェース・各データのメモリレイアウトは以下のようになります。
後に PyTorch 製のパラメータを設定することを考慮して、メモリレイアウトは PyTorch のものと揃えています。

  • 入力
    • x: 入力画像。shape=(in_features)
    • weight: 重み係数。shape=(out_features, in_features)
    • bias: バイアス値。 shape=(out_features)
  • 出力
    • y: 出力画像。shape=(out_features)
  • パラメータ:
    • in_features: 入力の次数
    • out_features: 出力の次数

全結合層では、内部で行われる演算の数は高々out_channels * in_channels 回となり、典型的なパラメータでは畳み込み層よりも圧倒的に低い演算回数です。

一方で重み係数に注目すると、畳み込み層がshape=(out_channels, in_channels, ksize, ksize) だったのに対し全結合層はshape=(out_features, in_features) となります。例えば畳み込み層から全結合層に変わるタイミングの層だと、in_features = channels * width * height の関係が成り立ちます。width, height >> ksize なことを考慮すると、多くの場合で全結合層のパラメータに必要なメモリ容量は畳み込み層のものを大きく上回ります。

FPGA では内部に潤沢な SRAM バッファを持つため、全体の計算量に対しメモリアクセス量が多いかつメモリ上のデータの再利用が多い処理は得意です。全結合層単体では重みデータの再利用は発生しませんが、動画像処理のような連続した処理では複数回の全結合が行われるため、この点はメリットとなります。

一方で、この記事のタイトルにもあるエッジ環境では小規模な FPGA が採用されるため、 SRAM 容量が足りず外部 DRAM へのアクセスが必要になってしまう場合があります。メモリ帯域に余裕がある場合はそのままアクセスしても良いですが、余裕がない場合は作成するモデルのパラメータチューニングや学習後のモデルに対して量子化や枝刈りと呼ばれるモデル圧縮手法を適用し、SRAM にパラメータを収める or DRAM 帯域の使用量を減らすことが重要となってきます。

プーリング層

プーリング層は入力画像を縮小する処理で、今回採用したのは2×2の MaxPooling と呼ばれる手法です。この処理では、入力画像の2×2領域の最大値を、出力画像の1ピクセル分の値とします。こちらも第2回の図を見るのが分かりやすいので再掲します。

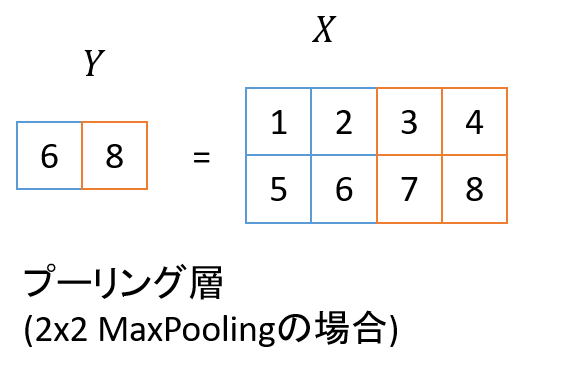
プーリング層でも入力画像は複数のチャネルを持ちますが、プーリング処理自体は各チャネルで独立に行われます。このため、プーリング層での入力画像のチャネル数と出力画像のチャネル数は常に等しくなります。

プーリング層の実装は以下になります。

void maxpool2d(const float *x, int32_t width, int32_t height, int32_t channels, int32_t stride, float *y) {
  for (int ch = 0; ch < channels; ++ch) {
    for (int32_t h = 0; h < height; h += stride) {
      for (int32_t w = 0; w < width; w += stride) {
        float maxval = -FLT_MAX;

        for (int bh = 0; bh < stride; ++bh) {
          for (int bw = 0; bw < stride; ++bw) {
            maxval = std::max(maxval, x[(ch * height + h + bh) * width + w + bw]);
          }
        }

        y[(ch * (height / stride) + (h / stride)) * (width / stride) + w / stride] = maxval;
      }
    }
  }
}

この関数のインターフェースは以下となります。この実装では端処理を省略しているため、画像の幅・高さは共に stride で割り切れる必要があります。

  • 入力
    • x: 入力画像。shape=(channels, height, width)
  • 出力
    • y: 出力画像。shape=(channels, height/stride, width/stride)
  • パラメータ:
    • width: 画像幅
    • height: 画像高さ
    • stride: 縮小倍率

ReLU

ReLU は単に負の値を0にするだけの処理ですので、非常にシンプルです。

void relu(const float *x, int64_t size, float *y) {
  for (int64_t i = 0; i < size; ++i) {
    y[i] = std::max(x[i], .0f);
  }
}

完全に要素ごとに独立した処理なので、x, y のメモリレイアウトは特に規定しません。

生成されるハードウェア

ここまでの内容で全ての層の関数が出来上がりました。前回の記事の手順と同様にすると、今回作成した関数も libtorch と同等の出力を生成することが確認できます。また、 Vivado HLS により RTL シミュレーションの通る回路が生成されます。ここからは、実際にどのような回路が生成されたかを簡単に説明していきます。

上記の linear 関数をそのまま Vivado HLS に入力するとエラーとなるので、以下のようにラップしたものを用いて今回は評価を行います。ここで、入出力をポインタ->配列としているのは、回路作成時に配列にアクセスするためのアドレスのビット幅を決定するためです。また、in_features の値を7*7*8=392, out_features の値を32 に固定しています。これはループ数が可変の場合に Vivado HLS の出力する性能が ? となってしまうのを回避するためです。

static const std::size_t kMaxSize = 65536;

void linear_hls(const float x[kMaxSize], const float weight[kMaxSize], 
                const float bias[kMaxSize], float y[kMaxSize]) {
  dnnk::linear(x, weight, bias, 7*7*8, 32, y);
}

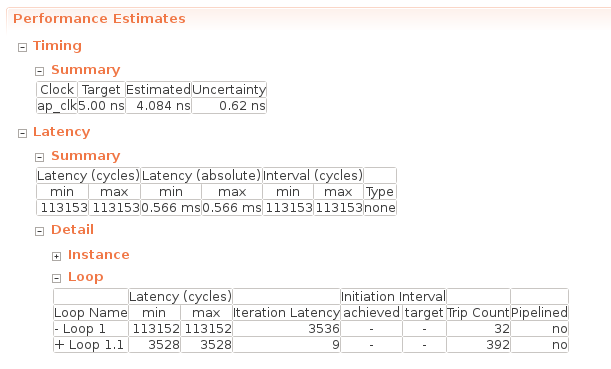
linear_hls 関数の合成レポートの “Performance Estimates” は以下のようになります。

Timing -> Summary には合成時に指定した動作周波数が書かれていて、今回は 5.00 ns = 200MHz が動作周波数となります。重要なのは Latency -> Summary の項で、この関数を実行した際のサイクル数単位のレイテンシ (Latency (cycles)) や、実時間単位のレイテンシ (Latency (absolute)) が記載されています。これを見ると、この全結合層は 0.566 ms で処理が完了することが分かります。

Latency -> Detail -> Loop の欄には、各ループに対し、1反復にかかるサイクル数 (Iteration Latency) やそのループの反復数 (Trip Count) が記載されています。Latency (cycles) には、Iteration Latency * Trip Count + ループ初期化コスト の値が格納されます。Loop 1 が out_features に対するループで、Loop 1.1 が in_features に対するループを表します。これを読むと、 Loop 1.1 で行われる sum += x[j] * weight[i * in_features + j]; という処理に9サイクル必要となっていることが分かります。

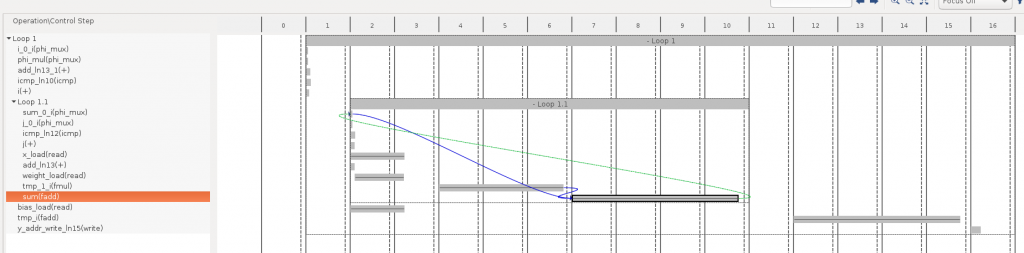
Vivado HLS の Schedule Viewer という機能を使うと、どの処理で時間がかかっているかがもう少し詳細に分かります。下の図の横軸の2~10が Loop 1.1 の処理内容を表し、大きく分けてx, weights 等のロードに2サイクル、乗算 (fmul) に3サイクル、加算 (fadd) に4サイクルで計9サイクルとなっているようです。

Vivado HLS による開発では、このコードに対して #pragma HLS pipeline を始めとする最適化指示子を追加していくことで、効率的なハードウェアを作るよう指示します。最適化内容としては、通常の FPGA 開発と同様にパイプライン化や演算器の並列化などが頻繁に用いられます。これらの最適化を行うと、Vivado HLS のレポートでは以下のようにして高速化できていることを確認できます。

  • パイプライン化: Iteration Latency の減少 (最小値=1)
  • 並列化: Trip Count の減少、Loop の削除

これまでも何度か述べている通り、今回のコースではまずは推論処理を FPGA で動かすことを目的とするため、上述したような最適化は行いません。どのような最適化が行えるか興味がある方は、以下の公式のチュートリアルやドキュメントを参考にすると良いです。

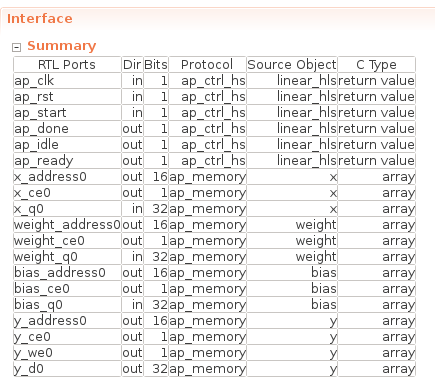
最後に、この関数のインターフェースは以下のようになります。

今回はインターフェースは特に指定していないため、x 等の配列インターフェースは ap_memory となっていて、これは FPGA 上では 1サイクルで読み書き可能なメモリ (BRAM / Distributed RAM) に該当します。次回の記事では各レイヤーの入出力を繋いでいきますが、その場合もこの例と同じように FPGA 内部のメモリを各レイヤー間のインターフェースとして繋いでいく予定です。

まとめ

今回の記事では全結合層、プーリング層、ReLU の実装をしました。これで全てのレイヤーの実装が完了したため、次回の記事ではこれらの層を結合します。その後、実際に MNIST のデータを与えて正しい推論ができることを確認していきます。

株式会社フィックスターズ シニアエンジニア 松田裕貴

タイトルとURLをコピーしました